1.1.5 Модели измерений. Фундаментальная система измерений и их решения. Анализ ошибок измерений.

Измерения обязательно связаны с о сравнением измеряемой величины с эталоном.

Прямое измерение – интересующий параметр получается непосредственно в процессе измерений.

Косвенное измерение – измеряется функция от измеряемой величины.

Измерительная система является сложной системой:

Объект измерения > Канал связи (<Шум) > Датчик сигнала

Датчик сигналов > Измерительное устройство (<Шум) > Результат 1го измерения

Результат первичных измерений > Система обработки измерений (<Ошибки вычисл.) > Результат

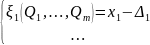
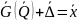- Фундаментальная система измерений.

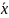- данные измерения - известны

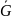- оператор измерительной системы, для данного подхода – известен.

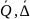- не известны.

В системе имеется 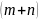– неизвестных.

Известен закон распределения ошибок. Будем считать, что ошибки отсутствуют. Поэтому, система превращается в 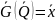, где неизвестных и уравнений.

Систему можно решить, если 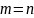, т.е. число измерений – минимальное.

- в общем случае нелинейная.

Поэтому имеется 2 метода решения: прямой и итерационный.

Прямой – метод, в результате которого получаются точные решения при отсутствии ошибок округления.

Итерационный – метод, в результате применения которого получается приближенное решение, поэтому обычно рассматриваются только сходящиеся итерационные процессы, в результате применения которого, можно получить результат с любой заданной точностью независимо от задания начальных условий (при отсутствии ошибок округления).

В ряде случаев итерационный процесс может привести к более точным результатам, т.к. отсутствуют ошибки.

1.1.6 Операторные уравнения. Нахождение псевдорешения. Обусловленность слау.

Пусть – оператор, действующий из m-мерного линейного пространства в n-мерное линейного пространство 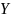, заданных над одним и тем же полем 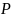. Определим все векторы 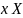, которые при заданных операторе и векторе 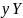удовлетворяют уравнению: 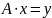. Это уравнение называется операторным уравнением, вектор 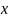– его решением, а вектор 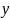– правой частью.

В общем виде СЛАУ можно записать в следующем виде:

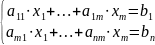
Используя выше приведенные определения, запишем СЛАУ в матричном виде:

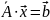
Решить СЛАУ значить найти такие значения вектора 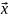подстановка которого в систему, обращает каждое уравнение этой системы в тождество.

Классификация СЛАУ

1. Если число уравнений больше чем число неизвестных, т.е. 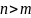, то СЛАУ называется переобусловленой.

2. Если число уравнений меньше чем число неизвестных, т.е. 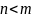, то СЛАУ называется недообусловленой.

3. Если число уравнений равно числу неизвестных, т.е. 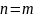, то СЛАУ называется нормальной.

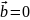4. Если вектор свободных членов равен нулю , то СЛАУ называется однородной.

5. Если вектор свободных членов не равен нулю 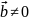, то СЛАУ называется неоднородной.

6. Если система, имеет хотя бы одно решение, она называется совместной. Система, не имеющая решений, называется несовместной.

7. Совместная система, имеющая единственное решение, называется определенной, а имеющая бесчисленное множество решений, называется неопределенной.

Очевидно, что однородная система всегда совместна, так как имеет хотя бы одно решение 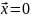, которое называется тривиальным.

Если система плохо обусловлена, то это значит, что погрешности коэффициентов матрицы и свободных членов или погрешность округления при расчетах могут сильно исказить решение.

Исходную систему уравнений с учетом погрешности в векторе 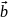можно записать в ви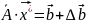де , где 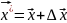. Абсолютную погрешность можно выразить подставив второе выражение в первое: .

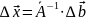Норма этой погрешности определяется соотношением: 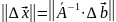или

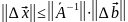
Относительная погрешность:

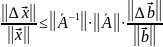
Вводим понятие числа обусловленности: 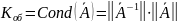. И тогда:

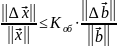
Следует иметь ввиду, что мы определяем предельную относительную погрешность, реальная может быть и меньше.

Решение СЛАУ по методу наименьших квадратов.

Для любого операторного уравнения имеется решение по методу наименьших квадратов 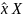, удовлетворяющее равенству: .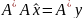

Выражение 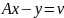– называется системой уравнений поправок.

Вектор решения системы нормальных уравнений 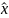называется псевдорешением уравнений поправок.

Т.к. нормальная система уравнений совместная, то она имеет или единственное решение, или множество решений.

Когда 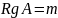, где – размерность пространства , псевдорешение единственно: ,

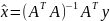когда же 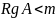, то нормальная система уравнений имеет множество решений.

Если решение нормальной системы уравнений не единственно, то при отсутствии какой – либо дополнительной информации о решении системы уравнений поправок, которая, как правило, может быть получена из физической сущности задачи или по дополнительным измерениям, за ее решение берется псевдорешение наименьшей длины, называемое нормальным псевдорешением: