МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ ПО КУРСУ

«МАТЕМАТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ИНЖЕНЕРНЫХ ЗАДАЧ»

(для студентов строительных специальностей)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ, МОЛОДЕЖИ И СПОРТА УКРАИНЫ

ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ

КАФЕДРА ВЫСШЕЙ И ПРИКЛАДНОЙ МАТЕМАТИКИ И ИНФОРМАТИКИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ ПО КУРСУ

«МАТЕМАТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ИНЖЕНЕРНЫХ ЗАДАЧ»

(для студентов строительных специальностей)

Утверждено Утверждено

на заседании научно- на заседании кафедры высшей и

методического совета прикладной математики и

информатики

Протокол № от . .2012г. Протокол № от . .2012г.

Макеевка 2012

УДК 681.3.06 (071)

ББК В161.6я73

Методические указания к выполнению лабораторных работ по курсу «Математические методы решения инженерных задач» (для студентов строительных специальностей) / Позднякович А. Е., Копычко О. Н., Моисеенко В. А., Акулов В. Ф. – ДонНАСА, 2012. – 33 с.

Методические указания содержат необходимый методический материал для|до| выполнения практических|практичных| заданий|задачи| с помощью|посредством| программного комплекса Mathcad| по курсу «Математические методы решения инженерных задач». Приведены|наведено| основные теоретические сведения|ведомость|, индивидуальные задания|задача|, примеры|приклад| выполнения работ и список литературы, что позволяет самостоятельно рассмотреть основные элементы данного курса.

Методические указания ориентированы|ориентируемый| на формирование предметной модели специалиста и адаптированы к|до| кредитно-модульной системе организации учебного процесса|.

Для студентов строительных специальностей Донбасской национальной академии строительства и архитектуры.

Guidance for practical work on the course "Mathematical methods solving of engineering tasks " (for students of building professions). // Eds.: Pozdnyakovich A.E., Kopychko O.N., Moiseenko V.A., Akulov V. F. - Makiyivka: DonNASA, 2012. - 33 p.

Guidance contain the necessary methodical material for carrying out practical tasks on engineering decision problems using Mathcad software system on the course " Mathematical methods solving of engineering tasks”. The basic theoretical information, individual tasks, examples of work and the list of literature, which allow to consider the basic elements of the theme ourselves, are in the guidance.

Guidance focuses on the formation of subject specialist model. Guidance is adapted to the credit-module system of learning process.

For students of building specialties of Donbas National Academy of Building and Architecture.

Составители: Позднякович А. Е., доц. к.ф.-м.н.,

Копычко О. Н., доц. к.ф.-м.н.,

Моисеенко В. А., доц. к.ф.-м.н.,

Акулов В. Ф. ассистент.

Рецензент: ________,

Ответственный за выпуск: ________

Содержание

1. Приближенное решение систем нелинейных уравнений 4

1. Метод Ньютона 4

1. Реализация метода Ньютона в|посредством| MathCad 7

2. Проекционные методы решения краевых задач для обыкновенных дифференциальных уравнений 10

   1. Метод Галеркина 11

   2. Реализация метода Галеркина в|посредством| MathCad 12

   3. Основные понятия метода конечных элементов 15

   4. Одномерный элемент с кусочно-линейными базисными функциями 17

   5. Пример 19

   6. Реализация метода конечных элементов в одномерном случае 23

Варианты индивидуальных заданий 30

Список рекомендованной литературы 32

1. Приближенное решение систем нелинейных уравнений

1.1. Метод Ньютона

Рассмотрим нелинейную систему уравнений

(1.1)

с действительными левыми частями.

Запишем короче систему (1.1). Совокупность аргументов можно рассматривать как - мерный вектор

.

Аналогично совокупность функций представляет собой также - мерный вектор (вектор-функцию)

.

Поэтому система (1.1) кратко записывается так:

. (1.1^/ )

Для решения системы (1.1^/ ) будем пользоваться методом последовательных приближений.

Предположим, что найдено -е приближение

одного из изолированных корней векторного уравнения (1.1^/ ).

Тогда точный корень уравнения (1.1^/ ) можно представить в виде

, (1.2)

где - поправка (погрешность корня).

Подставляя выражение (1.2) в уравнение (1.1^/ ), будем иметь:

. (1.3)

Предполагая, что функция непрерывно дифференцируема в некоторой области, содержащей и , разложим левую часть уравнения (1.3) по степеням малого вектора , ограничиваясь линейными членами,

. (1.4)

или, в развернутом виде,

(1.4^/ )

Из формул (1.4) и (1.4^/ ) вытекает, что под производной следует понимать матрицу Якоби системы функций относительно переменных , т.е.

,

или в краткой записи

.

Система (1.4^/) представляет собой линейную систему относительно поправок с матрицей , поэтому формула (1.4) может быть записана в следующем виде:

.

Отсюда, предполагая, что матрица - неособенная, получим:

.

Следовательно,

, (1.5)

где за можно взять грубое значение искомого корня.

При практическом применении метода Ньютона для решения нелинейных систем вычисления по формуле (1.5) прекращают, когда

. (1.6)

Итак, исходя из вышеизложенного, запишем алгоритм метода Ньютона:

1. Определяем начальное приближение .

2. Уточняем значение корня по формуле (1.5).

3. Если условие (1.6) выполняется, то задача решена и 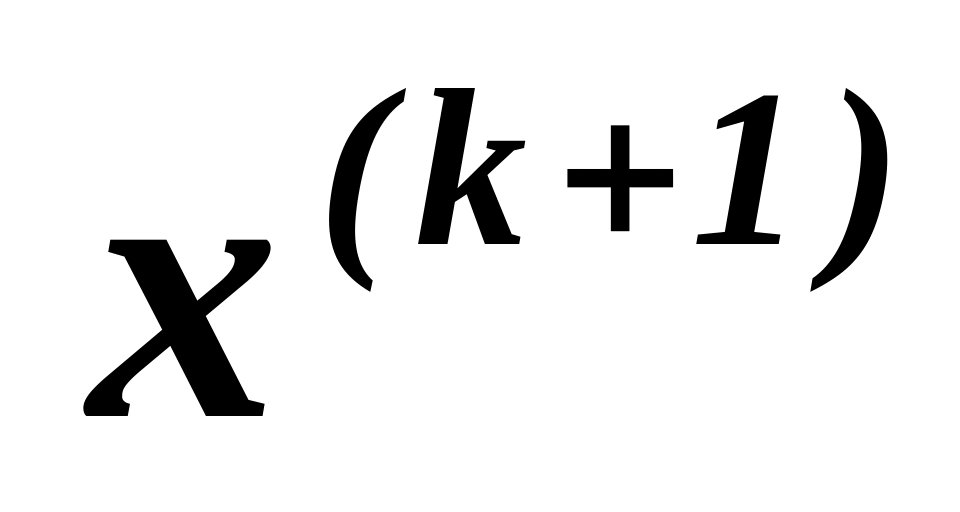- корни системы нелинейных уравнений, иначе переходим к п. 2.

Будем считать, что функции нелинейной системы (1.1^/ ) и матрица их производных уже определены, тогда блок-схема алгоритма решения этой системы имеет вид: