5. Главное значение несобственного интеграла

Как известно, для интеграла с двумя особенностями в точках и ,

а для интеграла с одной особенностью во внутренней точке

.

Главное значение несобственного интеграла обозначается буквами

Определение 4. По определению

, (2)

, (3)

если эти пределы существуют и конечны. В таком случае интеграл называется сходящимся в смысле главного значения.

Так как определение главного значения несобственного интеграла является частным случаем общего определения несобственного интеграла, то если несобственный интеграл сходится, то он сходится и в смысле главного значения, и его главное значение равно самому интегралу. Но возможны случаи, когда расходящийся несобственный интеграл сходится в смысле главного значения.

Пример. Найти главное значение несобственного интеграла .

Решение.

Известно, что расходится: , и в этих интегралах , но .

ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА

1. Собственные и несобственные интегралы, зависящие от параметра

Определение 5. Рассмотрим функцию

, (4)

где – некоторая функция двух переменных. Такой интеграл называется интегралом, зависящим от параметра, а переменная называется параметром.

При различных значениях правая часть формулы (4) дает различные значения интеграла (если этот интеграл вообще существует), поэтому этот интеграл действительно является функцией параметра .

Сначала рассмотрим обычные (как говорят, собственные) интегралы, зависящие от параметра.

Через обозначим замкнутый прямоугольник на плоскости : .

Приведем (без доказательства) основные свойства собственных интегралов, зависящих от параметра.

Теорема 4. Пусть функция непрерывна на прямоугольнике . Тогда функция непрерывна на отрезке .

Теорема 5. Пусть функция непрерывна на прямоугольнике . Тогда .

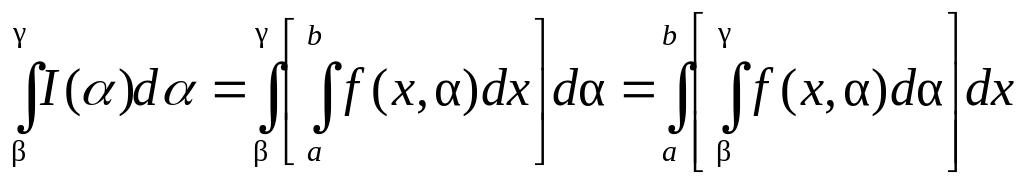Теорема 6. Пусть функции и непрерывны на прямоугольнике . Тогда при существует .

Пример. Вычислить интеграл .

Решение.

. Дифференцируем обе части по , используя теорему 6:

Теоремы 4 – 6 применять к несобственным интегралам возможно только при определенных условиях, которые мы в силу сложности этих условий и недостатка времени, разбирать не будем, ограничившись лишь примером.

Пример. Вычислить несобственный интеграл .

Решение.

Этот интеграл имеет одну особенность , так как в точке 0 функция имеет конечный предел: по правилу Лопиталя . Далее имеем: Первый из этих интегралов не является несобственным, т.е. равен некоторому числу, а второй сходится или расходится одновременно с интегралом , который сходится при : и сходится, так как . Значит сходится при

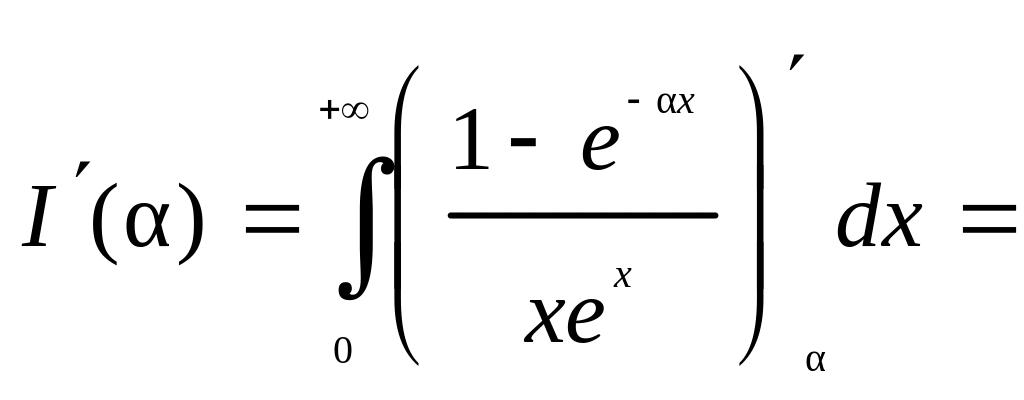
а так как то и

Конечно, нужно еще проверить правомерность наших выкладок.

2. Гамма-функция

Существует ряд функций, которые задаются (сходящимися) несобственными интегралами. В этом параграфе мы рассмотрим одну из таких функций.

Определение 6. Гаммафункцией называется функция , которая задается следующим несобственным интегралом:

. (5)

Данный интеграл является несобственным. У него две «особенности»: бесконечный предел ( ) и разрыв подынтегральной функции при х = 0 (если ). Докажем, что этот интеграл сходится при всех (т.е. формула (5) определяет гаммафункцию при ). По определению интеграла с несколькими «особенностями», его надо представить в виде суммы интегралов с одной «особенностью» в каждом:

.

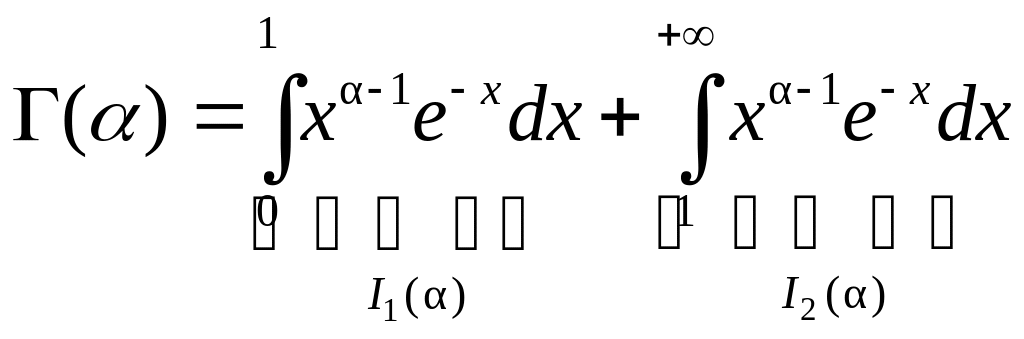1. Согласно теореме сравнения в предельной форме 2, сравним с : и сходится при сходится при (и расходится при ).

2. Докажем, что сходится при всех (фактически, это следует из того, что при стремится к нулю быстрее, чем в любой степени). Сравним, например, со сходящимся интегралом (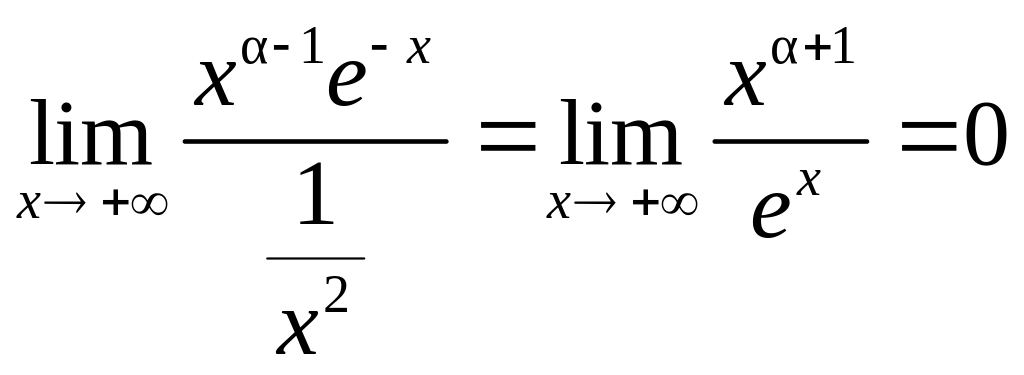если , то последнее равенство очевидно; если же , то нужно достаточное количество раз применить правило Лопиталя, при этом знаменатель не меняется, а из числителя , в конце концов, «уйдет», что и даст нужный нам результат), следовательно, по теореме сравнения в предельной форме 2 (случай ), сходится при всех .

3. Следовательно, сходится при и расходится при .

Нахождение значений гаммафункции ( )

1. Формула приведения

. (6)

▲ Применяя формулу интегрирования по частям, имеем:

. Здесь

,

. ■

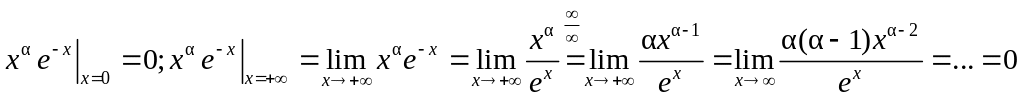2. Гамма-функция от 1

. (7)

▲ . ■

3. Гамма-функция натурального аргумента

(8)

▲ Пусть – натуральное число, тогда по формуле приведения

■

В частности, .

4. Гамма-функция от

. (9)

▲ . Сделаем замену , , . Тогда .

Замечание. . (10)

Это так называемый интеграл Эйлера-Пуассона; вычислить его в данный момент достаточно сложно; формула (10) будет доказана позднее, она будет получена путем перехода к полярным координатам в двойном интеграле. ■

5. Гамма-функция полуцелого аргумента

Введем обозначения: ; . Тогда справедлива следующая формула:

, . (11)

▲

. ■

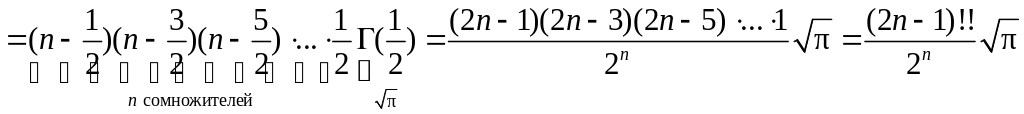Примеры. Вычислить значения и .

Решение.

; .

6. Гаммафункция отрицательного аргумента

До сих пор мы определяли гаммафункцию для положительных (лишь для них сходится ). Формула приведения может служить определением гаммафункции отрицательного аргумента. Из этой формулы

. (12)

Теперь, зная , мы находим . Если , то , а на этом интервале гаммафункция уже известна. Таким методом мы найдем гамма  функцию для . Точно так же, зная гамма  функцию при , по формуле (12) найдем гамма - функцию для и т.д. В итоге мы найдем гамма  функцию во всех отрицательных нецелых точках.

Получим формулу для гамма - функции в отрицательных полуцелых точках.

. (13)

Примеры. Найти значение гамма - функции в отрицательных полуцелых точках.

Решение.

; .

11