НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
1. Определение несобственного интеграла
Определение определенного интеграла как предела интегральных сумм теряет смысл в случаях бесконечных пределов интегрирования (так как тогда интегральная сумма содержит бесконечное число слагаемых) или неограниченной подынтегральной функции (так как интегрируемая функция обязательно ограничена). В этих случаях дается определение несобственного интеграла. Вначале дадим его в случае, когда так называемая особенность (это бесконечный предел интегрирования или точка бесконечного разрыва подынтегральной функции) – одна и находится на правом краю промежутка интегрирования.
Определение 1.
Пусть функция
определена
на полуинтервале
и интегрируема на любом отрезке
,
где
(т.е.
существует).
По определению
,
(1)
если этот предел существует и конечен. В этом случае несобственный интеграл называется сходящимся. В противном случае (предел не существует или бесконечен) несобственный интеграл называется расходящимся.
В частности,
,
для неограниченной при
функции.
Аналогично по
определению
,
если
интегрируема в любом
,
где
.
Если интеграл имеет несколько особенностей, то он представляется в виде суммы интегралов с одной особенностью на краю в каждом и называется сходящимся, если сходится каждый из этих интегралов. В этом случае значение всего интеграла не зависит от расположения точек деления.
Геометрический смысл, свойства и вычисление несобственных интегралов
Всюду для
определенности будет предполагаться,
что интеграл имеет только одну особенность
в точке
.
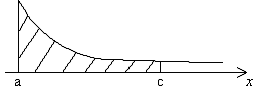
1. Геометрический смысл
Пусть
неотрицательна
и непрерывна на
,
что по определению считается площадью
соответствующей бесконечной области
(см., например, рис. ниже).
2. Формула Ньютона-Лейбница
Пусть
непрерывна на
и
– ее
первообразная на этом
полуинтервале,
тогда
.
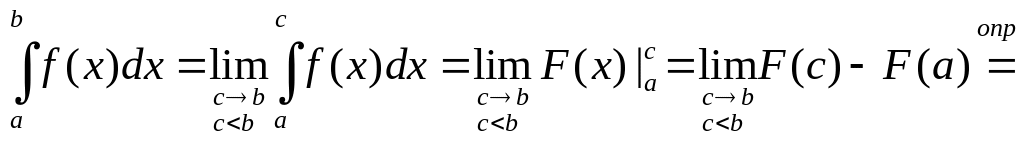
Таким образом,
где
.
При этом левая и правая части этой формулы конечны или бесконечны одновременно.
Примеры. Исследовать
на сходимость несобственные интегралы
и
.
Решение.
1) при
этот предел существует и конечен при
и бесконечен
при
;
если же
,
то
т.е.
сходится при
и расходится при
;
2) при
этот предел существует и конечен при
и бесконечен
при
;
если же
,
то
т.е.
сходится при
и расходится при
Эти же выводы верны
и для
и
.
3. Линейность
Если
и
сходятся, то сходится и
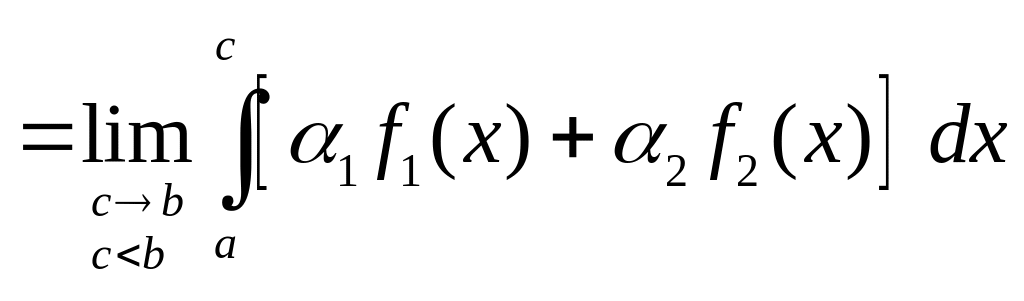
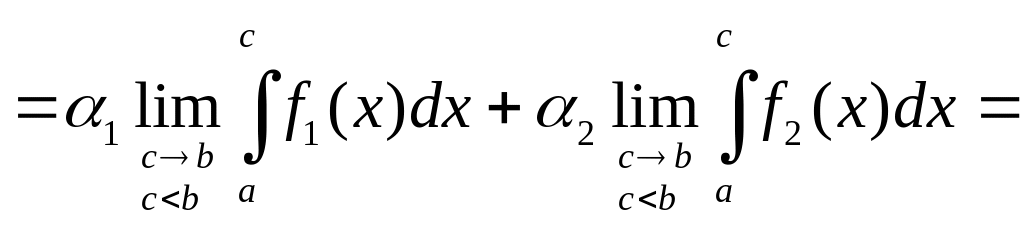
4. Аддитивность
,
если несобственный
интеграл
сходится и
.
5. Интегрирование неравенств
Пусть
и
сходятся и для
Так как
для
то, переходя в этом неравенстве к пределу
при
имеем
.
6. Интегрирование по частям
Если
и
непрерывно дифференцируемы на
и
сходятся несобственные интегралы
и
,
то
,
.
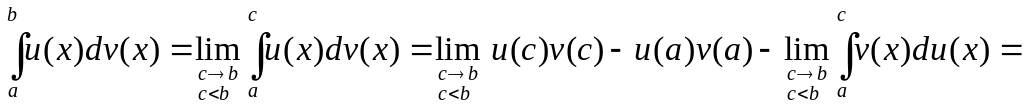
7. Замена переменной
Пусть
непрерывна
на
;
где
непрерывно дифференцируема на
;
,
при
существует обратная функция
непрерывно дифференцируемая при
.
Тогда
(так как при
и
).
При этом интегралы в левой и правой
частях этой формулы (если они являются
несобственными) сходятся или расходятся
одновременно.