3. Оценка качества эконометрической модели

Существует несколько показателей, характеризующих качество модели регрессии, т.е. степень соответствия построенной модели исходным данным.

Парный линейный коэффициент корреляции оценивает качество линейной модели парной регрессии:

где S_x - среднеквадратическое отклонение факторной переменной; S_y - среднеквадратическое отклонение результативной переменной.

Можно выделить несколько особенностей парного корреляционного коэффициента:

1) коэффициент изменяется в пределах [-1;+1]. Если r_yx  [0;+1], то связь между переменными прямая. Если r_yx  [-1;0], то связь между переменными обратная. Если r_yx = 0, то связь между переменными отсутствует;.

2) регрессионный анализ между изучаемыми переменными не проводится, если r_yx = 1 или r_yx = -1.

Коэффициент детерминации r_yx² рассчитывается как квадрат парного линейного коэффициента корреляции r_yx. Коэффициент детерминации характеризует в процентном отношении зависимость вариации результативной переменной от вариации факторной переменной в общем объёме вариации.

3. Для оценки качества линейной множественной модели регрессии используется множественный коэффициент корреляции между результативной переменной у и несколькими факторными переменными х, характеризующий степень тесноты связи между ними:

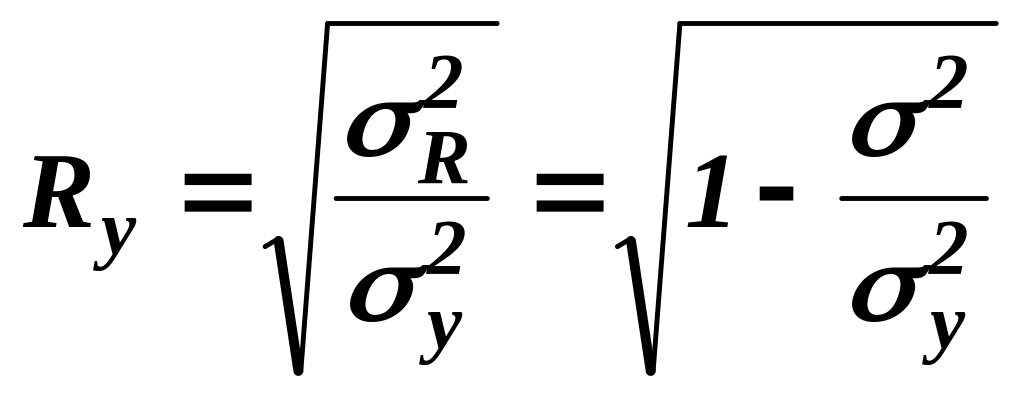
где σ²_y - общая дисперсия результативной переменной;

σ²_R - объяснённая дисперсия результативной переменной;

σ ² - необъяснённая дисперсия результативной переменной.

4. Теоретический коэффициент детерминации R²_у рассчитывается как квадрат множественного линейного коэффициента корреляции R_у.

5. Среднеквадратическая ошибка модели регрессии:

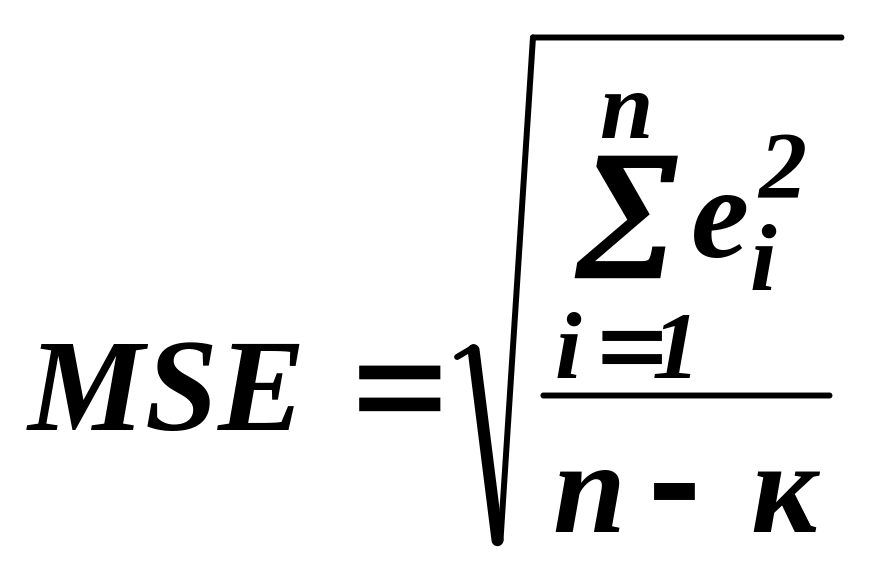
где к - число коэффициентов модели регрессии. Модель регрессии считается качественной, если среднеквадратическая ошибка меньше показателя среднеквадратического отклонения наблюдаемых значений результативной переменной от модельных значений (рассчитанных по модели регрессии).

Проверка гипотезы о значимости коэффициентов модели парной регрессии является весьма важным этапом перед практическим использованием построенной модели регрессии. Значимость коэффициентов означает их значимое отличие от нуля.

Выдвинутые гипотезы проверяются с помощью t-статистики или t-критерия Стьюдента. При этом наблюдаемое значение t-критерия t_набл сравнивают со значением t-критерия, определяемым по таблице распределения Стьюдента, или с критическим значением t_крит.

Критическое значение t-критерия t_крит(α; n-k) зависит от уровня значимости и числа степеней свободы.

Уровень значимости α определяется как α = 1 – γ, где величина γ называется доверительной вероятностью попадания оцениваемого параметра в доверительный интервал. Доверительную вероятность необходимо брать близкую к единице (0,95, 0,99).

Число степеней свободы определяется как разность между объёмом выборки (n) и числом оцениваемых параметров по данной выборке (k). Для модели парной линейной регрессии число степеней свободы равно (n - 2), так как по выборке оцениваются только два параметра b₀ и b₁.

Наблюдаемое значение t-критерия Стьюдента для проверки гипотезы Н₀:b₀ = 0:

где b₀ - оценка коэффициента модели регрессии ₀ ;

S_b0 - величина стандартной ошибки коэффициента модели регрессии ₀.

Наблюдаемое значение t-критерия Стьюдента для проверки гипотезы Н₀:b₁ = 0:

где b₁ - оценка коэффициента модели регрессии ₁;

S_b1- величина стандартной ошибки коэффициента модели регрессии ₁.

Если |t_набл| > t_крит, т.е. модуль наблюдаемого значения t-критерия больше критического значения t-критерия, то с вероятностью (1 – α) основная гипотеза о незначимости коэффициентов модели регрессии отвергается (коэффициенты модели регрессии значимо отличаются от нуля).

Если |t_набл| ≤ t_крит, т.е. модуль наблюдаемого значения t-критерия меньше или равен критическому значению t-критерия, то с вероятностью α основная гипотеза о незначимости коэффициентов модели регрессии принимается (коэффициенты модели регрессии почти не отличаются от нуля или равны нулю).

Значимость парного коэффициента корреляции между факторной переменной х и результативной переменной у означает его значимое отличие от нуля.

Основной гипотезой, выдвигаемой при проверке значимости коэффициента корреляции, является гипотеза Н₀, о незначимости полученного коэффициента: Н₀:r_yx = 0. Обратной (или альтернативной) является гипотеза Н₁ о значимости парного коэффициента корреляции: Н₁: r_yx ≠ 0.

Выдвинутые гипотезы проверяются с помощью t-статистики или t-критерия Стьюдента в том случае, если объём выборки достаточно велик (n ≥ 30) и коэффициент корреляции по модулю значительно меньше единицы 0,45 ≤ | r_yx | ≤ 0,75. Наблюдаемое значение t-критерия t_крит сравнивают со значением t-критерия, определяемым по таблице распределение Стьюдента, или с критическим значением t_крит.

Критическое значение t-критерия определяется по таблице распределений t-критерия Стьюдента:

t_крит(α; n – к) ,

где α - уровень значимости; к - число оцениваемых по выборке коэффициентов; (n - к) - число степеней свободы.

Наблюдаемое значение t-критерия Стьюдента для проверки гипотезы Н₀:r_yx = 0 в случае линейной модели парной регрессии:

где r_ух парный коэффициент корреляции между переменными х и у.

Если |t_набл| > t_крит, т.е. модуль наблюдаемого значения t-критерия больше критического значения t-критерия, то с вероятностью (1 - α) основная гипотеза о незначимости парного линейного коэффициента корреляции отвергается. Между переменными х и у существует корреляционная связь, которую можно оценить с помощью построения модели парной регрессии.

Если |t_набл| ≤ t_крит т.е. модуль наблюдаемого значения t-критерия меньше или равен критическому значению t-критерия, то с вероятностью α основная гипотеза о незначимости коэффициента корреляции принимается.

Значимость линейной модели парной регрессии зависимости между факторной переменной х и результативной переменной у означает её значимое отличие от нуля. Проверка гипотезы о значимости модели регрессии равнозначна проверке гипотез о значимости парного коэффициента детерминации r²_xy или коэффициентов регрессии β₀ и β₁.

Если значимость модели парной регрессии проверяется через значимость парного коэффициента детерминации, то выдвигается основная гипотеза Н₀: r_yx = 0 о незначимости данного коэффициента и, следовательно, о незначимости модели парной регрессии е целом. Обратной (или альтернативной) является гипотеза Н₁: r_yx ≠ 0 о значимом отличии от нуля парного коэффициента детерминации и, следовательно, о значимости построенной модели парной регрессии.

Если значимость модели парной регрессии проверяется через значимость коэффициентов регрессии, то выдвигаются основные гипотезы Н₀:₀ = 0 и Н₀:₁ = 0 и, следовательно, о незначимости модели парной регрессии в целом. Обратными (или альтернативными) являются гипотезы Н₁:₀ ≠ 0 и Н₁: ₁ ≠ 0 о значимом отличии от нуля коэффициентов регрессии и, следовательно, о значимости построенной модели парной модели.

Для проверки гипотезы о значимости модели парной регрессии в целом используется F-критерий Фишера-Снедекора. При этом наблюдаемое значение F-критерия F_набл сравнивают с критическим значением F-критерия F_крит, определяемым по таблице распределения Фишера-Снедекора.

Наблюдаемое значение F-критерия для проверки гипотезы о незначимости линейной модели парной регрессии:

.

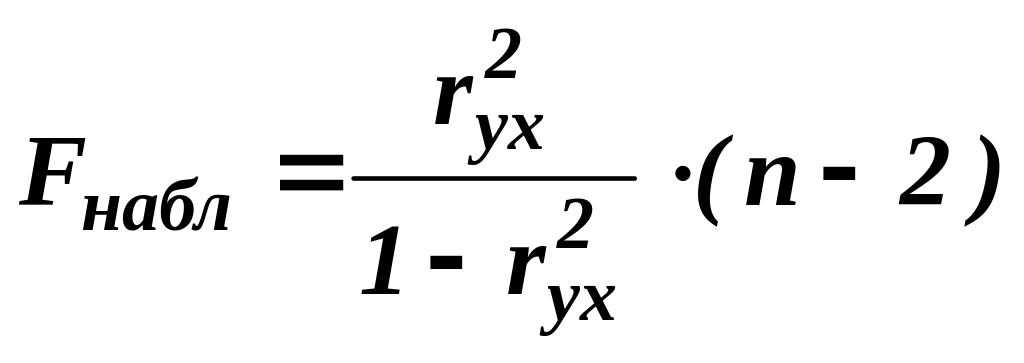Критическое значение F-критерия определяется по таблице распределения Фишера-Снедекора в зависимости от уровня значимости α и числа степеней свободы: k₁ = к - 1 и k₂ = n – к, где n - объём выборочной совокупности, к - число оцениваемых по выборке коэффициентов. При проверке значимости модели парной регрессии критическое значение F-критерия рассчитывается как F_крит(α; 1; n – 1).

Если F_набл > F_крит, т.е. наблюдаемое значение F-критерия больше критического значения данного критерия, то с вероятностью α основная гипотеза о незначимости парного коэффициента детерминации или коэффициентов модели регрессии отвергается, и модель парной регрессии значимо отличается от нуля.

Если F_набл < F_крит т.е. наблюдаемое значение F-критерия меньше критического значения данного критерия, то с вероятностью (1 – α) основная гипотеза о незначимости парного коэффициента детерминации или коэффициентов модели регрессии принимается, и полученная модель парной регрессии является незначимой.

Точечный и интервальный прогнозы для модели парной регрессии.

Одной из основных функций построенной модели парной регрессии является дальнейшее её применение в экономических расчетах. В большинстве случаев модели регрессии используют для расчета прогнозного значения результативной переменной при заданном значении факторной переменной.

Точечный прогноз результативной переменной у при заданном значении факторной переменной х_k в случае линейной модели парной регрессии рассчитывается по формуле:

= b₀ + b₁x_k + e_k

Точечная оценка прогноза результативной переменной с доверительной вероятностью (1 - α) попадает в интервал прогноза, который определяется по формуле:

– t·S ≤ y_k^* ≤ + t· S ,

где y_k^* - прогнозное значение результативной переменной; t - t-критерий Стьюдента, который определяется в зависимости от заданного уровня значимости α и числа степеней свободы (n - 2) для модели парной регрессии; S - величина ошибки прогноза в точке k:

,

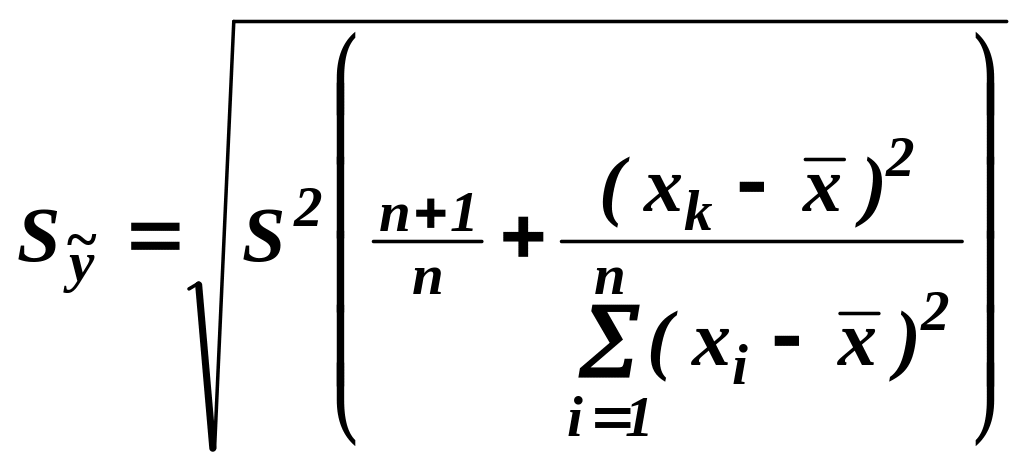где S² - несмещённая оценка дисперсии случайной ошибки линейной модели парной регрессии σ²(); n - объём выборочной совокупности.

Линейная модель множественной регрессии используется для характеристики формы связи между результативной (зависимой) переменной и несколькими факторными (независимыми) переменными.

При построении нормальной (классической) линейной модели множественной регрессии учитываются следующие пять условий:

1) х_1i … х_mi, - неслучайные и независимые переменные;

2) E(_i)=0, где i = 1, 2 … n, т.е. математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях;

3) D() = Е(_i²) = σ² = const, т.е. дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений;

4) соv(_i , _j) = Е(_i _j) = 0, где i ≠ j, т.е. случайные ошибки модели регрессии не коррелируют между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю). Это условие не выполняется для временных рядов;

5) _i - N(0,σ²) т.е. случайная ошибка модели регрессии - случайная величина, подчиняющаяся нормальному закону распределения с нулевым математическим ожиданием и дисперсией σ².

Общий вид линейной модели множественной регрессии:

y_i = β₀ + β₁ x_1i +…+ β_n x_ni + _i

где у_i – значение i-ой результативной переменной, i=1,2 … n;

x_1i … х_mi - значения факторных переменных;

β₀ … β_n, неизвестные коэффициенты модели множественной регрессии; _i - случайные ошибки модели множественной регрессии.

Матричный вид линейной модели множественной регрессии:

Y = XB + 

где Y - вектор значений результативной переменной размерности n1; Х - вектор значений факторной переменной размерности n(m+1). Первый столбец является единичным, поскольку в модели регрессии коэффициент β₀ умножается на единицу; B - вектор неизвестных коэффициентов размерности (m+1)1;  - вектор случайных ошибок размерности n1.

Добавление в модель такого компонента, как вектор случайных ошибок, необходимо в связи с практической невозможностью оценить связь между переменными со стопроцентной точностью.

Классический метод наименьших квадратов для модели множественной регрессии.

Предположим, что между несколькими факторными переменными х и результативной переменной у существует линейная связь, которая описывается равенством:

y_i = β₀ + β₁ x_1i +…+ β_m x_mi + _i

где у_i - значение i-ой результативной переменной, i=1,2…n;

х_i1...х_mi - значения факторных переменных; β₀…β_m - неизвестные коэффициенты модели множественной регрессии; _i - случайные ошибки модели множественной регрессии.

Неизвестные коэффициенты линейной модели множественной регрессии β₀…β_m оцениваются с помощью классического метода наименьших квадратов (МНК), основная идея которого заключается в определении такого вектора оценки β, который минимизировал бы сумму квадратов отклонений (остатков) наблюдаемых значений результативной переменной у от модельных значений (рассчитанных на основании построенной модели регрессии).

Для модели множественной регрессии в общем случае минимизируется функционал вида:

.

Решением системы нормальных уравнений будут МНК-оценки неизвестных коэффициентов модели множественной регрессии вида:

B = (X^TX)^-1X^TY.

Применение соизмеримых показателей тесноты связи возможно из-за несопоставимости единиц измерения факторных переменных. К соизмеримым показателям тесноты связи относят коэффициенты частной эластичности и стандартизированные частные коэффициенты регрессии.

Коэффициент частной эластичности рассчитывается по формуле:

где Х_i - среднее значение факторной переменной х_i по выборке, i = 1,2…n;Y - среднее значение результативной переменной у по выборке; - первая производная у по х.

Частный коэффициент эластичности характеризует процентное изменение результативной переменной у при намерении на 1% от среднего уровня факторной переменной х, при постоянном значении остальных факторных переменных, участвующих в модели регрессии.

Частный коэффициент эластичности для линейной модели множественной регрессии определяется по формуле:

где β_i - коэффициент модели множественной регрессии.

Частный коэффициент корреляции оценивает взаимосвязь между результативной переменной и одной из факторных переменных при постоянном значении остальных факторных переменных, включённых в модель регрессии.

Следовательно, частный коэффициент корреляции позволяет исключить влияние на результативную переменную всех факторных переменных, кроме одной.

Определим частные коэффициенты корреляции на примере линейной модели регрессии с двумя факторными переменными:

y_i = β₀ + β₁ x_i + β₂ z_i + _i

где у_i - результативная переменная, i = 1,2…n;

х_i - первая факторная переменная; z_i - вторая факторная переменная; β₀, β₁, β₂ - неизвестные коэффициенты модели регрессии; _i - случайная ошибка модели регрессии.

Частные коэффициенты корреляции позволяют оценить степень зависимости между результативной переменной у_i и первой факторной переменной х_i при постоянном значении второй факторной переменной z_i, и наоборот, оценить степень зависимости между результативной переменной у_i и второй факторной переменной z_i при постоянном значении первой факторной переменной х_i.

Подобные частные коэффициенты корреляции называются коэффициентами первого порядка, потому что исключается влияние только одной факторной переменной. Порядок частного коэффициента корреляции определяется количеством переменных, влияние которых исключается.

Частный коэффициент корреляции между переменными у и х при постоянном значении переменной z определяется по формуле:

где r_yx , r_yz , r_xz - обычные парные коэффициенты корреляции.

Коэффициент множественной корреляции используется для оценки совокупного влияния всех факторных переменных, включенных в модель множественной регрессии, на результирующую переменную.

Определим коэффициент множественной корреляции для линейной модели множественной регрессии с m факторными переменными.

Общий вид линейной модели множественной регрессии:

y_i = β₀ + β₁ x_1i +…+ β_m x_mi + _i

где у_i - значение i-ой результативной перемен i = 1, 2, ... n;

х_ji - значение факторных переменных, i = 1, 2,...n, j = 1, 2,…m; β₀, β_m - неизвестные коэффициенты модели множественной регрессии; _i – случайные ошибки модели множественной регрессии.

Коэффициент множественной корреляции характеризуется следующими свойствами:

1) он изменяется в пределах [0; +1] и поэтому не используется для определения направления связи между результативной переменной и факторными переменными;

2) между результативной и факторными переменными существует сильная взаимосвязь если значение множественного коэффициента корреляции близко к единице. Если значение множественного коэффициента корреляции близко к нулю, то между результативной и факторными переменными существует слабая взаимосвязь.

Коэффициент множественной детерминации характеризует, на сколько процентов построенная модель регрессии объясняет разброс значений результативной переменной относительно её среднего значения.

Коэффициент множественной детерминации рассчитывается как квадрат коэффициента множественной корреляции.

Коэффициент множественной детерминации также называется количественной характеристикой объясненной построенной моделью множественной регрессии дисперсии результативной переменной. Чем больше значение коэффициента множественной детерминации, тем лучше модель регрессии описывает анализируемую взаимосвязь между переменными.

Коэффициент множественной детерминации можно рассчитать на основании теоремы о разложении сумм квадратов.

Сумма квадратов разностей между значениями результативной переменной и её средним значением по выборке может быть представлена следующим образом:

= +

где - общая сумма квадратов модели множественной регрессии с n переменными (Total Sum of Squares - TSS); - сумма квадратов остатков модели множественной регрессии с n переменными (Error Sum of Squares – ESS); сумма квадратов объясненной регрессии модели множественной регрессии с n переменными (Regression Sum of Squares - RSS).

Коэффициент множественной детерминации, рассчитанный через теорему о разложении сумм квадратов:

R²(y, x₁…x_n) = 1- ESS/TSS

Воздействие на качество дополнительно включенной в модель регрессии факторной переменной не всегда можно определить с помощью обычного коэффициента множественной детерминации. Для этой цели рассчитывается скорректированный (adjusted) коэффициент множественной детерминации, в котором учитывается количество факторных переменных в модели регрессии:

,

где n - количество наблюдений в выборочной совокупности;

к - число оцениваемых коэффициентов в модели регрессии.

При большом объёме выборки значения обычного и скорректированного коэффициентов множественной детерминации практически не отличаются

Значимость частного коэффициента корреляции между факторной переменной х_i и результативной переменной у означает его значимое отличие от нуля.

Основной гипотезой, выдвигаемой при проверке значимости частного коэффициента корреляции, является гипотеза Н₀ о незначимости полученного коэффициента: Н₀:r(ух_i/х₁....х_n-1) = 0. Обратной является гипотеза H₁, о значимости частного коэффициента корреляции: Н₁:r(ух_i/х₁....х_n-1) ≠ 0. Гипотезы проверяются с помощью t-статистики или t-критерия Стьюдента.

Критическое значение t-критерия, определяемое по таблице распределений t-критерия Стьюдента:

t_крит(α/2; n-к-1),

где α/2 - уровень значимости; n - объём выборки; к - число оцениваемых по выборке коэффициентов; (n–к–1) – степень свободы.

Наблюдаемое значение t-критерия Стьюдента для проверки гипотезы Н₀:r(ух_i/х₁....х_n-1) = 0:

.

Если |t_набл| > t_крит, то с вероятностью (1 - α) основная гипотеза о незначимости частного коэффициента корреляции отвергается. Между переменными х_i и у существует корреляционная связь при постоянных значениях остальных факторных переменных, включенных в модель.

Если |t_набл| ≤ t_крит, то с вероятностью α основная гипотеза о незначимости частного коэффициента корреляции принимается. Между переменными х_i и у отсутствует корреляционная связь при постоянных значениях остальных факторных переменных, включённых в модель.

Основной гипотезой, выдвигаемой при проверке значимости частного коэффициента корреляции, является гипотеза Н₀ о незначимости полученного коэффициента: Н₀:R(ух_i) = 0, i = 1, 2, …, n. Обратной является гипотеза Н₁ о значимости коэффициента множественной корреляции: Н₁:R(ух_i) ≠ 0.

Гипотезы проверяются с помощью F-статистики или F-критерия Фишера.

Критическое значение F-критерия определяется по таблице распределения Фишера-Снедекора:

F_крит(α; k₁; k₂),

где α - уровень значимости; k₁ = к - 1 и k₂ = n – к – число степеней свободы,.

Наблюдаемое значение F-критерия Фишера для проверки гипотезы Н₀:R(ух_i) = 0,:

,

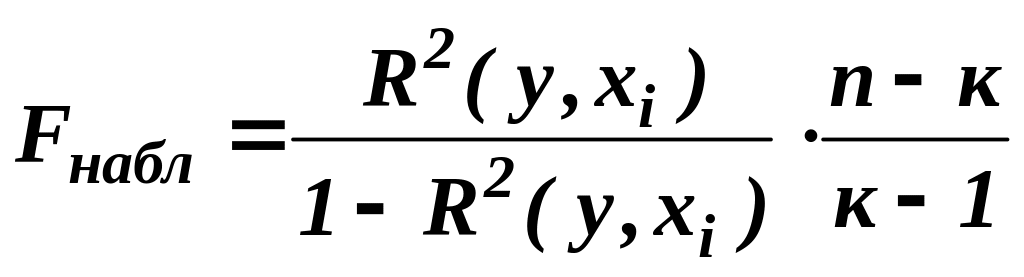где R²(у, х_i) - коэффициент множественный детерминации.

Если F_набл > F_крит, то с вероятностью α основная гипотеза о незначимости коэффициента множественной регрессии отклоняется, и он признается значимым.

Основной гипотезой, выдвигаемой при проверке значимости коэффициентов регрессии, является гипотеза Н₀ о незначимости полученных коэффициентов:

.

Обратной является гипотеза Н₁ о значимости коэффициентов регрессии: .

Гипотезы проверяются с помощью t-статистики или t-критерия Стьюдента, который рассчитывается через частный F-критерий Фишера. Между этими критериями существует взаимосвязь, используемая при проверке значимости коэффициентов модели множественной регрессии:

,

Критическое значение t-критерия: t_крит(α; n-к-1),

где α - уровень значимости; n - объем выборки; к - число оцениваемых по выборке коэффициентов; (n - к - 1) - степень свободы, определяемая по таблице распределений t-критерия Стьюдента.

Наблюдаемое значение частного F-критерия для проверки гипотезы

.

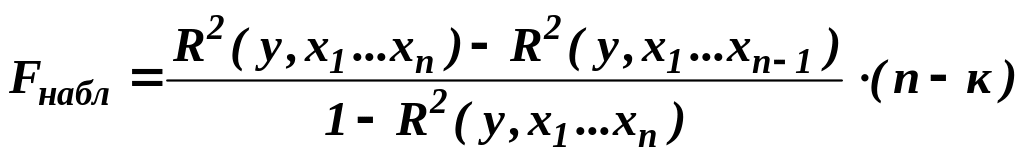Если t_набл ≥ t_крит, то основная гипотеза о незначимости коэффициентов модели множественной регрессии отклоняется,

Если t_набл < t_крит, то основная гипотеза о незначимости коэффициентов модели множественной регрессии принимается.

Проверка гипотезы о значимости модели множественной регрессии состоит в проверке гипотезы о значимости множественного коэффициента корреляции или значимости коэффициентов модели регрессии. В большинстве случаев значимость модели множественной регрессии проверяется через значимость коэффициента множественной корреляции.

Основной гипотезой, выдвигаемой при проверке значимости модели множественной регрессии, является гипотеза Н₀ о её незначимости: Н₀:r(ух_i/х₁....х_n-1) = 0.

Гипотезы проверяются с помощью F-критерия Фишера. Критическое значение F-критерия определяется по таблице распределения Фишера-Снедекора: F_крит(α; k₁; k₂),

где α - уровень значимости; k₁ = к – 1; k₂ = n – к - число степеней свободы,.

Наблюдаемое значение F-критерия для проверки гипотезы Н₀:r(ух_i/х₁....х_n-1) = 0:

где R²(y, х_i) – коэффициент множественной детерминации.

Если F_набл > F_крит, то с вероятностью α основная гипотеза о незначимости коэффициента множественной корреляции отклоняется, и модель множественной регрессии признается значимой.

Последствия мультиколлинеарности и методы её обнаружения.

Мультиколлинеарность - это нарушение первой предпосылки линейной модели множественной регрессии о независимости факторных переменных х_1i, ... х_mi, включённых в модель.

Мультиколлинеарность в матричном виде - это зависимость между столбцами матрицы факторных переменных Х.

Основная причина мультиколлинеарности заключается в неправильном подборе факторных переменных х_1i, ... х_mi, включённых в модель.

Последствия, к которым может привести наличие мультиколлинеарности в модели множественной регрессии:

1) основная гипотеза о незначимости коэффициентов множественной регрессии в большинстве случаев подтверждается, однако сама модель регрессии при проверке с помощью F-критерия оказывается значимой;

2) полученные оценки коэффициентов модели множественной регрессии неоправданно завышены или имеют неправильные знаки;

3) добавление или исключение из исходных данных одного-двух наблюдений оказывает сильное влияние на оценки коэффициентов модели регрессии;

4) наличие мультиколлинеарности в модели множественной регрессии может сделать её непригодной для дальнейшего применения (например, для построения прогнозов).

С целью обнаружения мультиколлинеарности анализируется корреляционная матрица факторных переменных R.

Корреляционная матрица факторных переменных - это симметричная относительно главной диагонали матрица линейных парных коэффициентов корреляции факторных переменных:

где r_ij - коэффициент парной линейной корреляции между i-ой и j-ой факторными переменными, i,j =1,2, ... n.

Если в корреляционной матрице факторных переменных есть парный коэффициент корреляции между i-ой и j-ой переменными r>0,8, то в модели множественной регрессии присутствует мультиколлинеарность.

Если собственное число корреляционной матрицы факторных переменных λ_max<10^-5, то в модели множественной регрессии присутствует мультиколлинеарность.

Если отношение собственных чисел корреляционной матрицы факторных переменных λ_min/λ_max<10^-5, то в модели множественной регрессии присутствует мультиколлинеарность.

Если при прогнозировании результативной переменной величина ошибки прогноза является удовлетворительной, то модель множественной регрессии можно использовать и при наличии мультиколлинеарности. Если же прогноз получается неудовлетворительным, то мультиколлинеарность необходимо устранять.

Сбор дополнительных данных - простой способ устранения мультиколлинеарности, однако на практике это не всегда возможно.

Метод преобразования переменных - это способ замены всех переменных, включенных в модель. Например, вместо значений результативной переменной и факторных переменных можно взять их логарифмы. Тогда модель множественной регрессии имеет вид:

.ln y = b₀ + b₁ln x₁ + b₂ln x₂ + e.

Однако этот метод не гарантирует устранения мультиколлинеарности.

Метод пошагового включения факторных переменных в модель регрессии – это метод определения из возможного набора факторных переменных именно тех, которые усилят качество модели регрессии.

Суть метода пошагового включения состоит в том, что из числа всех факторных переменных в модель регрессии включаются переменные, имеющие наибольший модуль парного линейного коэффициента корреляции с результативной переменной. При добавлении в модель регрессии новых факторных переменных их значимость проверяется с помощью F-критерия Фишера. Если F_набл > F_крит, то включение факторной переменной в модель множественной регрессии является обоснованным. Проверка факторных переменных на значимость осуществляется до тех пор, пока не найдётся хотя бы одна переменная, для которой не выполняется условие F_набл > F_крит.

Гетероскедастичность - это явление неоднородности дисперсий случайных ошибок (остатков) модели регрессии (рис. 2).

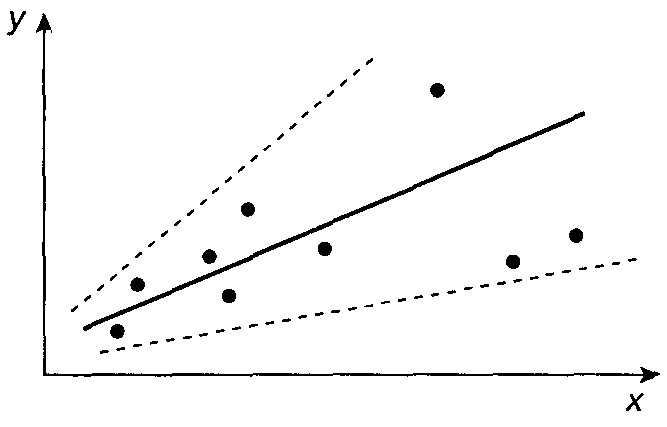
Рис. 2. Случай гетероскедастичности остатков

Случайная ошибка модели регрессии - это величина отклонения в модели линейной множественной регрессии:

_i = y_i – β₀ – β₁x_1i – …– β_mx_mi.

Величина случайной ошибки модели регрессии неизвестна, поэтому вычисляется выборочная оценка случайной ошибки модели регрессии:

е_i = y_i – – b₀ – b₁x_1i –…– b_mx_mi,

где е_i - остатки модели регрессии. Одно из условий нормальной линейной модели множественной регрессии заключается в том, что D(_i) = Е(_i ²) = σ² = const, т.е. дисперсия случайной ошибки модели регрессии является постоянной для всех наблюдений, данное условие называется гомоскедастичностью дисперсий случайных ошибок модели регрессии.

Гомоскедастичность - это ситуация постоянства дисперсии случайной ошибки е_i для всех i наблюдений модели регрессии.

Но на практике условие гомоскедастичности случайной ошибки _i, или остатков модели регрессии е_i не всегда выполняется. Поэтому предположение о разнородности дисперсий случайных ошибок для всех i наблюдений модели регрессии выглядит так:

D(_i) ≠ Е(_i ²) ≠ σ² ≠ const,

где i ≠ j.

Условие гетероскедастичности можно выразить через ковариационную матрицу:

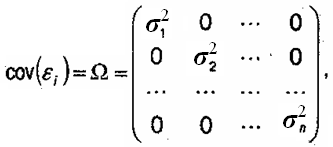
где σ₁² ≠ σ₂² ≠…≠ σ_n².

Последствия гетероскедастичности остатков модели регрессии:

1) оценки нормальной линейной модели регрессии остаются несмещенными и состоятельными, но теряется эффективность;

2) появляется вероятность неверного вычисления оценок стандартных ошибок коэффициентов модели регрессии, что может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.

Обнаружить гетероскедастичность остатков модели регрессии можно путем проверки гипотез.

Основной Н₀ является гипотеза о гомоскедастичности остатков модели регрессии Н₀:σ₁²=σ₂²=…=σ_n²=σ². Обратной, или альтернативной, является гипотеза Н₁ о гетероскедастичности остатков модели регрессии

Н₁:σ₁² ≠ σ₂² ≠…≠ σ_n²

В основе теста Голдфелда-Квандта обнаружения гетероскедастичности остатков модели регрессии лежит предположение о нормальном законе распределения случайной ошибки _i модели регрессии.

Тест Голдфелда-Квандта проводится в несколько этапов.

1. Предположим, что на основе выборочных данных была построена линейная модель множественной регрессии:

у_i = b₀ + b₁x_1i + b₂x_2i + b₃x_3i + e_i

где у_i - результативная переменная, i = 1,2…, n;

x_mi - факторные переменные (m = 1, 2, 3; i=1,2…, n);

b₀, b₁, b₂, b₃ - неизвестные коэффициенты модели регрессии;

e_i - случайная ошибка модели регрессии.

2. В модели множественной регрессии выбирается факторная переменная x_mi (m = 1, 2, 3; i=1,2…, n), от которой могут зависеть остатки модели е_i. Значения переменной x_mi ранжируются, располагаются по возрастанию и делятся на три части.

3. Для первой и третьей частей строятся две независимые модели регрессии:

у_i¹ = b₀¹ + b₁¹x_1i + b₂¹x_2i + b₃¹ x_3i , где i = 1,…,n’;

у_i³ = b₀³ + b₁³x_1i + b₂³x_2i + b₃³ x_3i где i = n’+1,…,n

4. По каждой из построенных моделей регрессий рассчитываются суммы квадратов остатков:

5. Осуществляется проверка основной гипотезы об отсутствии гетероскедастичности в основной модели множественной регрессии через F-критерий Фишера.

Критическое значение F-критерия, определяемое по таблице распределения Фишера-Снедекора

F_крит(α; k₁; k₂),

где α - уровень значимости; k₁ = n’- к и k₂ = n’- к - степени свободы; к - количество оцениваемых коэффициентов в основной модели регрессии,.

Наблюдаемое значение F-критерия:

если ESS³ > ESS¹;

или

если ESS¹ > ESS³;

Если F_набл > F_крит, то основная гипотеза отклоняется, и в основной модели регрессии присутствует гетероскедастичность, зависящая от факторной переменной x_mi.

Если F_набл ≤ F_крит, то основная гипотеза принимается, и гетерскедастичность в основной модели регрессии не зависит от факторной переменной x_mi.

Взвешивание членов модели регрессии - это наиболее простой метод устранения гетероскедастичности остатков модели регрессии. Суть состоит в том, что отдельным наблюдениям результативной переменной у_i с максимальным среднеквадратическим отклонением случайной ошибки придаётся больший вес, а остальным наблюдениям результативной переменной у_i с минимальным среднеквадратическим отклонением случайной ошибки придается меньший вес.

Процесс взвешивания параметров модели регрессии осуществляется в несколько этапов.

1. Предположим, что по данным выборочной совокупности была построена линейная модель парной регрессии вида:

В данной модели регрессии доказано наличие гетероскедастичности остатков, т.е. σ²(_i) ≠ σ²(_j),

где i ≠ j.

2. Разделим все члены модели регрессии на среднеквадратическое отклонение случайной ошибки S(_i).

Общий вид процесса взвешивания для модели парной регрессии:

, i = 1, 2,…, n

3. Полученную модель регрессии приведем к линейному виду с помощью метода замен:

Запишем модель регрессии в линеаризованном виде:

Полученная модель регрессии является моделью с двумя факторными переменными - u_i и z_i.

4. Дисперсия случайной ошибки взвешенной модели регрессии определяется по формуле:

Данное равенство говорит о постоянстве дисперсий случайных ошибок преобразованной модели регрессии, т.е., о присутствии условия гомоскедастичности остатков модели регрессии.

Главная проблема метода взвешивания членов модели регрессии - необходимость априорного знания среднеквадратических отклонений случайных ошибок модели регрессии.

Автокорреляция - это корреляция, которая возникает между уровнями исследуемой переменной, т.е. корреляция во времени. Свойство автокорреляции чаще всего проявляется во временных рядах.

Автокорреляция остатков модели регрессии е_i (или случайных ошибок модели регрессии _i) - это корреляционная зависимость между настоящими и прошлыми значениями остатков.

Временной лаг - это величина сдвига между рядами остатков модели регрессии. Величина временного лага определяет порядок коэффициента автокорреляции.

Например, если существует корреляционная зависимость между остатками е_n и е_n-2, то величина временного лага равняется двум. Следовательно, данную зависимость будет характеризовать коэффициент автокорреляции второго порядка между рядами остатков е₁...е_n-2 и е₃.. .е_n.

Одно из условий нормальной линейной модели регрессии заключается в том, что cov(_i,_j) = E(_i _j) = 0, где i ≠ j, т.е. случайные ошибки модели регрессии не коррелированы между собой, ковариация случайных ошибок любых двух разных наблюдений равна нулю. Нарушение этого условия приводит к автокорреляции остатков модели регрессии.

Последствий автокорреляции остатков модели регрессии аналогичны последствиям гетероскедастичности остатков модели регрессии:

1) оценки нормальной линейной модели регрессии остаются несмещенными и состоятельными, но теряется эффективность;

2) появляется вероятность неверного вычисления оценок стандартных ошибок коэффициентов модели регрессии, что может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.

Применение автокорреляционной и частной автокорреляционной функций - это наиболее простой способ обнаружения автокорреляции остатков модели регрессии.

Автокорреляционная функция (АКФ) - это функция оценки коэффициента автокорреляции в зависимости от величины временного лага между исследуемыми рядами.

Коррелограмма - это график автокорреляционной функции. На коррелограмме отражаются коэффициенты автокорреляции (и их стандартные ошибки) для последовательности лагов из определенного диапазона (например, от 1 до 15). По оси Х откладываются значения τ (тау) - величины сдвига между рядами остатков. Значение τ совпадает с порядком автокорреляционного коэффициента.

Частная автокорреляционная функция (ЧАКФ) - это более глубокое понятие обычной АКФ. ЧАКФ на конкретном лаге отличается от обычной АКФ на величину удаленных автокорреляций с меньшими временными лагами, т.е. ЧАКФ даёт более точную картину автокорреляционных зависимостей остатков модели.

Для обнаружения автокорреляции первого порядка (между соседними рядами данных) остатков модели регрессии применяется критерий Дарбина-Уотсона.

Предположим, что по выборочным данным была построена модель множественной регрессии:

Y= XB + _t.

Ошибка, возникшая в связи с наличием в модели регрессии автокорреляции первого порядка, может быть представлена выражением:

_t = _t-1,

где ρ - коэффициент автокорреляции первого порядка, |ρ| < 1;

v_t - независимые, одинаково распределенные случайные величины с нулевым математическим ожиданием и дисперсией σ²(v_t). Для подтверждения наличия в модели регрессии автокорреляции первого порядка необходимо проверить значимость коэффициента автокорреляции первого порядка ρ (его значимое отличие от нуля).

При проверке значимости коэффициента автокорреляции первого порядка основной Н₀ является гипотеза о незначимости данного коэффициента: Н₀:ρ₁= 0. Обратной, или альтернативной, является гипотеза Н₁ о значимости коэффициента автокорреляции первого порядка: Н₁:ρ₁ ≠ 0.

Выдвинутые гипотезы проверяются с помощью критерия Дарбина-Уотсона.

Критическое значение критерия Дарбина-Уотсона d_крит(n; к–1) определяется с помощью специальных таблиц, в которых указаны значения верхней d₁, и нижней d₂ границы критерия. Данные границы рассчитываются на основании объёма выборки n и числа степеней свободы (к - 1), где к - количество оцениваемых по выборке коэффициентов.

Наблюдаемое значение критерия Дарбина-Уотсона d_набл для проверки гипотезы Н₀:ρ₁= 0:

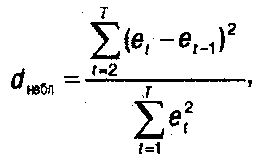
где е_t остатки модели регрессии в наблюдении t, e_t-1 - остатки модели регрессии в наблюдении t-1:

Приближённое значение величины критерия Дарбина-Уотсона можно также вычислить по формуле: d_набл2(1-r₁),

где r₁ - выборочный коэффициент автокорреляции первого порядка.

Устранение автокорреляции остатков модели регрессии - это необходимый этап в оценивании модели регрессии в связи c теми негативными последствиями, к которым может привести корреляционная зависимость между значениями случайных ошибок.

Авторегрессионная схема первого порядка - это метод устранения автокорреляции первого порядка между соседними членами ряда остатков в линейных моделях регрессии либо моделях регрессии, сводящихся к линейному виду. Для практического использования данной схемы необходимо знать величину коэффициента автокорреляции. Поскольку величина коэффициента автокорреляции ρ₁ неизвестна, то в качестве его оценки используется выборочный автокорреляционный коэффициент остатков первого порядка r₁:

Предположим, что на основе выборочных данных была построена модель парной регрессии, содержащая автокорреляцию остатков первого порядка:

y_t = β₀ + β₁x_t + _t

Модель регрессии в момент времени t с учётом процесса автокорреляции остатков первого порядка может быть представлена в виде:

y_t = β₀ + β₁x_t + _t-1 + v_t

где ρ - коэффициент автокорреляции, |ρ| < 1;

v_t - независимые, одинаково распределенные случайные величины с нулевым математическим ожиданием и дисперсией σ²(v_t).

Модель регрессии в момент времени (t-1) можно представить в виде:

y_t-1 = β₀ + β₁x_t-1 + _t-1

Если модель регрессии в момент времени (t-1) умножить на коэффициент автокорреляции первого порядка ρ и вычесть его из исходной модели регрессии в момент времени t, то получим преобразованную модель регрессии с учётом автокорреляции первого порядка:

y_t -  y_t-1 = β₀ (1-) + β₁(x_t -  x_t-1) + v_t

Для упрощения модели регрессии воспользуемся методом замен:

Y_t = y_t -  y_t-1; X_t = x_t -  x_t-1; Z_t= 1-.

С учётом замен модель регрессии может быть представлена в виде:

Y_t = Z_t β₀ + β₁X_t + v_t

Случайная ошибка v_t модели регрессии не подвержена процессу автокорреляции, поэтому автокорреляцию остатков модели регрессии можно считать устранённой.

Авторегрессионную схему первого порядка можно применить ко всем строкам матрицы исходных данных Х, кроме первого наблюдения. Но отсутствие значений Y₁ и Х₁ в небольшой выборочной совокупности может привести к неэффективности оценок коэффициентов модели регрессии.

Обобщённый метод наименьших квадратов. Нормальная линейная модель регрессии характеризуется выполнением двух условий о случайных ошибках:

1) D(_i) = Е(_i) = σ² = const, т.е. дисперсия случайной ошибки модели регрессии является величиной, постоянной для всех наблюдений;

2) cov(_i, _j) = Е(_i _j) = 0, где i ≠ j, т.е. ошибки модели регрессии не коррелированы между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю).

При наличии в модели регрессии гетероскедастичности остатков нарушается первое из указанных условий, т.е. D(_i) ≠ D(_j) ≠ σ² ≠ const, i ≠ j. При условии наличия в модели регрессии автокорреляции остатков нарушается второе условие, т.е. cov(_i, _j) ≠ Е(_i _j) ≠ 0.

Обобщенная модель регрессии - это модель регрессии, для которой не выполняются вышеперечисленные условия о случайных ошибках.

Матричный вид обобщённой линейной модели

Y = XB + ,

где Х - неслучайная матрица факторных переменных;

 - случайная ошибка модели регрессии с нулевым математическим ожиданием Е() = 0 и дисперсией σ²()Ω, _i ~ N(0, σ² Ω); Ω - ковариационная матрица случайных ошибок обобщённой модели регрессии.

Ковариационная матрица в обобщённой модели регрессии строится, исхода из условия непостоянства дисперсий остатков модели регрессии D(_i) ≠ D(_j) ≠ σ² ≠ const:

Для получения оценок неизвестных коэффициентов модели регрессии с гетероскедастичными или коррелированными случайными ошибками, удовлетворяющих свойствам состоятельности, несмещённости и эффективности, используется обобщенный метод наименьших квадратов (ОМНК).

Теорема Айткена. В классе линейных несмещённых оценок неизвестных коэффициентов обобщённой модели регрессии оценка будет иметь наименьшую ковариационную матрицу.

Общая формула для расчёта матрицы ковариаций ОМНК-оценок коэффициентов обобщенной модели регрессии:

Оценка величины σ²() рассчитывается по формуле:

Проверка гипотез о значимости коэффициентов обобщённой модели регрессии и модели регрессии в целом осуществляется с помощью тех же статистических критериев, что и в случае нормальной линейной модели регрессии.

Если в обобщённой модели регрессии случайные ошибки автокоррелированны, но гомоскедастичны, то для определения оценок неизвестных коэффициентов регрессии используется доступный обобщенный метод наименьших квадратов (ДОМНК).

Оценки неизвестных коэффициентов обобщённой модели регрессии рассчитываются с помощью ДОМНК по формуле:

где - оценка матрицы ковариаций случайных ошибок обобщённой модели регрессии.

Обобщённая модель парной регрессии с автокоррелированными, но гомоскедастичными случайными ошибками:

y_t = β₀ + β₁x_t + _t

Предположим, что случайные ошибки полученной модели регрессии подчиняются авторегрессионному процессу первого порядка. Тогда исходную модель регрессии можно представить в виде:

y_t = β₀ + β₁x_t + _t-1 + v_t

где ρ - коэффициент автокорреляции первого порядка, |ρ| < 1;

v_t - независимые, одинаково распределённые случайные величины с нулевым математическим ожиданием и дисперсией σ²(v_t).

Математическое ожидание случайной ошибки обобщённой модели регрессии:

E(_t) =E(_t-1 + v_t ) = E(_t-1) + E(v_t) = 0.

Дисперсия случайной ошибки обобщённой модели регрессии:

Ковариация между двумя случайными ошибками модели регрессии ₂ и ₁.

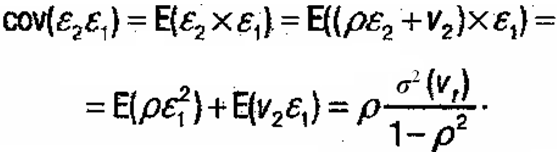
Ковариация между следующими случайными ошибками модели регрессии ₃ и ₁.

Дальнейший процесс расчета ковариаций продолжается для всех случайных ошибок обобщённой модели регрессии по тому же принципу.

В результате проведенных расчётов получим ковариационную матрицу случайных ошибок обобщённой линейной модели регрессии:

Величина σ²(v_t) является дисперсией случайной ошибки модели регрессии.

Модели регрессии с переменной структурой. Фиктивные переменные.

В большинстве случаев в модель регрессии включаются количественные факторные переменные. Однако при проведении некоторых исследований может возникнуть необходимость во включении в модель регрессии качественных факторных переменных (таких например, образование, возраст, пол и т.д.).

Фиктивная переменная - это атрибутивная, или качественная, факторная переменная, которая представлена с помощью определённого цифрового кода.

Модель регрессии с переменной структурой - это модель регрессии, которая включает в качестве факторной переменной (факторных переменных) фиктивную переменную.

В качестве примера модели регрессии с переменной структурой можно привести модель регрессии размера заработной платы (результативная переменная у от стажа работников с различным образованием (факторная переменная х).

Факторная переменная «образование» является качественной. Она может принимать три значения:

1) среднее образование;

2) среднее специальное образование;

3) высшее образование.

Для включения факторной переменной «образование» в модель регрессии используются только две фиктивные переменные, потому что фиктивных переменных в модель регрессии должно быть на единицу меньше, чем значений качественной факторной переменной.

Фиктивные переменные, характеризующие факторную переменную «образование»:

В результате получим модель регрессии с переменной структурой вида:

y = β₀ + β₁x + β₂ D₁ + β₃ D₂.

Данная модель регрессии называется моделью регрессии без ограничений.

Если все значения фиктивных переменных в модели регрессии равны нулю (D₁=D₂=0), то модель регрессии вида: у = β₀+β₁х называется базисной моделью регрессии, или моделью регрессии с ограничениями.

Частная модель регрессии заработной платы работников со средним специальным образованием от стажа:

у = β₀+β₁х+β₂D₁.

Коэффициент β₂ показывает, насколько большую заработную плату получают рабочие со средним специальным образованием по сравнению с рабочими со средним образованием при одинаковом стаже работы.

Частная модель регрессии заработной платы работников с высшим образованием от стажа:

у = β₀+β₁х+β₃D₂.

Коэффициент β₃ показывает, насколько большую заработную плату получают рабочие с высшим образованием по сравнению с рабочими со средним образованием при одинаковом стаже работы.

Тест Чоу - это метод который позволяет проверить предположение необходимости разбиения основной выборочной совокупности на части, или подвыборки.

Предположим, что на основании выборочных данных была построена основная модель регрессии без ограничений UN, т.е. все фиктивные переменные, включенные в данную модель, не равны нулю. В качестве подвыборок основной модели регрессии без ограничений будем считать частные модели регрессии.

Введем следующие обозначения:

РR₁ - первая подвыборка (первая частная модель регрессии);

РR₂ - вторая подвыборка (вторая частная модель регрессии);

ЕSS(РR₁) - сумма квадратов остатков для первой подвыборки;

ЕSS(РR₂) - сумма квадратов остатков для второй подвыборки;

ЕSS(UN) - сумма квадратов остатков для основной модели регрессии без ограничений;

ESS^UN_PR1 - сумма квадратов остатков для наблюдений первой подвыборки в основной модели регрессии без ограничений;

ESS^UN_PR2 - сумма квадратов остатков для наблюдений второй подвыборки в основной модели регрессии без ограничений.

Для частных моделей регрессии должны выполняться следующие условия:

ESS(PR₁)< ESS^UN(PR₁); ESS(PR₂)< ESS^UN(PR₂), или

(ESS(PR₁)+ ESS(PR₂))< ESS(UN).

Значимость частных моделей регрессии определяется с помощью F-критерия Фишера.

При проверке значимости частных моделей регрессии основной Н₀ является гипотеза о том, что качество основной модели регрессии без ограничений лучше качества частных моделей регрессии, или подвыборок. Обратной, или альтернативной, является гипотеза Н₁.

Критическое значение F-критерия Фишера, определяемое по таблице распределения Фишера-Снедекора:

F_крит(α; k₁; k₂),

где α - уровень значимости; k₁=m+1 и k₂=n-2m-2 – степени свободы; m - количество факторных переменных (в том числе фиктивных); n - объём общей выборочной совокупности.

Наблюдаемое значение F-критерия:

где ESS(UN) - ESS(PR₁) - ESS(PR₂) - величина, характеризующая улучшение качества модели регрессии после разделения её на подвыборки; m - количество факторных переменных (в том числе фиктивных); n - объем общей выборочной совокупности.

Если F_набл > F_крит, то основная гипотеза отклоняется, и качество частных моделей регрессии превосходит качество основной модели регрессии без ограничений.

Если F_набл ≤ F_крит, то основная гипотеза принимается, и нет необходимости разбивать основную модель регрессии без ограничений на подвыборки.

Спецификация переменных - это проблема отбора наиболее важных факторных переменных при построении модели регрессии.

Последствия неправильной спецификации переменных: исключение существенных и включение несущественных факторных переменных.