С.В. Амелин

ЭКОНОМЕТРИКА

Учебное пособие

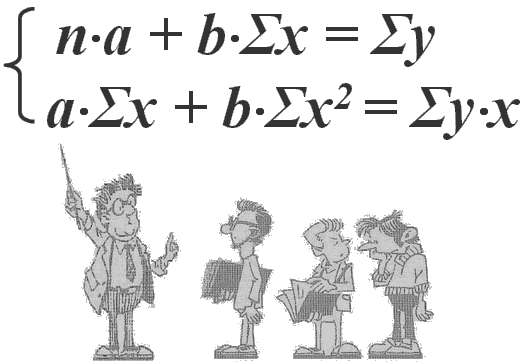
Воронеж - 2009

Гоувпо «Воронежский государственный технический университет»

С.В. Амелин

ЭКОНОМЕТРИКА

Утверждено Редакционно-издательским советом

университета в качестве учебного пособия

Воронеж 2009

УДК 330(075.8)

Амелин С.В. Эконометрика: учеб. пособие / С.В. Амелин. Воронеж: ГОУВПО «Воронежский государственный технический университет», 2009. 96 с.

Представлены основные разделы эконометрического моделирования, необходимые экономистам (руководителям и специалистам) для анализа, прогнозирования и обоснования управленческих решений в сложных производственно-экономических ситуациях.

Издание соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 080100 «Экономика», дисциплине «Эконометрика».

Издание предназначено для студентов направления 080100 «Экономика» дневной формы обучения, изучающих дисциплину «Эконометрика».

Ил. 2. Библиогр.: 20 назв.

Научный редактор д-р экон. наук, проф. О.Г. Туровец

Рецензенты: кафедра информационных технологий и математических методов Воронежского государственного университета (зав. кафедрой д-р экон. наук, проф. В.В. Давнис);

канд. экон. наук, доц. И.Н. Щепина

© Амелин С.В., 2009

© Оформление. ГОУВПО

“Воронежский государственный

технический университет”, 2009

Введение

В процессе проведения эконометрического моделирования важное значение имеет определение параметров моделей при анализе зависимостей между экономическими показателями.

Эконометрика - это наука, которая на базе статистических данных дает количественную характеристику взаимозависимым экономическим явлениям и процессам.

Зарождение эконометрики является следствием междисциплинарного подхода к изучению экономики. Эконометрика представляет собой сочетание трёх наук:

1) экономической теории;

2) математической и экономической статистики;

3) математики.

На современном этапе развития науки неотъемлемым фактором развитие эконометрики является развитие компьютерных технологий и специальных пакетов прикладных программ.

Для решения задач эконометрики используют статистические пакеты программ для компьютеров, значительная часть которых специально создана для эконометрического анализа. Так, задачи эконометрики могут быть решены с помощью функций анализа данных в среде электронных таблиц Мiсrоsoft Exсеl.

1. Линейная регрессионная модель

Понятие, цели и задачи эконометрики, типы данных.

Термин эконометрика» имеет в своей основе два слова: «экономика» и «метрика» (от гр. metron – “метод расчета определения расстояния между двумя точками в пространстве”). В общем случае эконометрику можно определить как науку об экономических измерениях.

Закономерности в экономике выражаются в виде математических моделей, характеризующих связи между различными показателями. Такие модели могут быть получены путём обработки статистических данных методами математической статистики с учётом случайных факторов.

Эконометрика - это наука, изучающая количественные закономерности и связи в экономике методами математической статистики. Предмет исследования эконометрики - это массовые экономические процессы и явления. Многие из эконометрических методов изучения социально-экономических закономерностей позаимствованы из статистики, однако специально для эконометрики были разработаны дополнительно значительное количество методов, которые не применяются в статистике.

Цель эконометрики - количественная характеристика экономических закономерностей, выявляемых экономической теорией в общих чертах. Задачи эконометрики - построить модели, выражающие эти закономерности, оценить их параметры, проверить гипотезы о закономерностях изменения и связях экономических показателей. Методы эконометрики основаны на представлениях теории вероятностей и математической статистики.

Задачи, решаемые с помощью эконометрики, классифицируются по трем признакам:

1) по конечным прикладным целям:

а) задачи прогноза социально-экономических показателей, характеризующих состояние и развитие изучаемой системы;

б) задачи моделирования возможных вариантов социально-экономического развития системы для определения параметров, которые оказывают наиболее сильное влияние на состояние системы в целом;

2) по уровню иерархии:

а) задачи макроуровня (страна в целом);

б) задачи мезоуровня (уровень отраслей, регионов);

в) задачи микроуровня (уровень фирмы, семьи, предприятия);

3) по области решения проблем изучаемой экономической системы:

а) задачи изучения рынка;

б) задачи изучения инвестиционной, социальной, финансовой политики;

в) задачи изучения ценообразования;

г) задачи изучения распределительных отношений;

д) задачи изучения спроса и потребления;

е) задачи изучения отдельно выделенного комплекса проблем.

Решение перечисленных задач эконометрики осуществляется с использованием математических моделей, построенных на основе эмпирических данных.

Эконометрический анализ служит основой для прогнозирования, которое необходимо для обоснования принятия управленческих решений.

Эконометрика как наука является следствием междисциплинарного подхода к изучению экономики. На современном этапе своего развития эконометрика представляет собой сочетание трёх наук: 1) экономической теории; 2) математики; 3) математической и экономической статистики.

Помимо этого, одним из основных факторов развития эконометрики является развитие компьютерных технологий и специализированных пакетов прикладных программ. Следовательно, эконометрика с помощью статистических и математических методов анализирует экономические закономерности, доказанные экономической теорией.

Экономические процессы могут характеризоваться двумя типами данных, обработка которых выполняется в процессе эконометрического анализа. Это пространственные данные и временные ряды.

Пространственные данные - это относящиеся к одному и тому же моменту времени данные о каком-либо экономическом показателе, характеризующем однотипные объекты. Например, данные об объеме производства на разных предприятиях промышленности за один и тот же период времени или о количестве работников разных предприятий промышленности в один и тот же момент времени.

Временные ряды - это данные о каких-либо показателях, характеризующих одни и те же объекты в различные моменты времени. Например, ежемесячные данные об объеме промышленного производства в стране или данные о количестве безработных в стране на начало календарного года за последние 10 лет. Особенность временных данных - временных рядов состоит в упорядоченности их во времени.

Существуют определенные отличия временного ряда или ряда динамики от пространственной выборки:

1) элементы ряда динамики естественным образом упорядочены во времени в отличие от пространственных данных;

2) элементы ряда не являются статистически независимыми в отличие от элементов случайной пространственной выборки, те, они подвержены зависимости между прошлыми и настоящими наблюдениями временного ряда (автокорреляции);

3) элементы ряда динамики не являются одинаково распределенными величинами.

Набор переменных - это совокупность экономической информации, характеризующей изучаемый процесс или объект. В эконометрической модели используются:

1) результативные (зависимые) переменные, которые в эконометрике называются объясняемыми переменными;

2) факторные (независимые) переменные, которые в эконометрике называются объясняющими переменными.

Среди экономических переменных, включённых в эконометрическую модель, выделяют:

1) экзогенные (независимые) переменные (х), значения которых задаются извне. В определённой степени данные переменные являются управляемыми;

2) эндогенные (зависимые или взаимозависимые) переменные (у), значения которых определяются внутри модели;

3) лаговые (экзогенные или эндогенные) переменные, которые относятся к предыдущим моментам времени и находятся в уравнении с переменными, относящимися к текущему моменту времени. Например, х_t-1 - лаговая экзогенная переменная, у_t-1 - лаговая эндогенная переменная;

4) предопределенные (объясняющие) переменные, к которым относятся лаговые (х_t-1) текущие (х) экзогенные переменные и лаговые эндогенные переменные (у_t-1)

Основная цель эконометрического моделирования - это характеристика значений одной или нескольких текущих эндогенных переменных в зависимости от значений предопределённых (объясняющих) переменных.

Экономические данные включают случайную составляющую, поэтому для их анализа и обработки применяются методы математической статистики.

Классы эконометрических моделей.

Существует три основных класса эконометрических моделей.

1. Регрессионные модели с одним уравнением, в которых результативная (зависимая) переменная у может быть представлена в виде функции факторных (независимых) переменных х₁ ... х_n:

y = f(x, β) = f(x₁…x_n, β₁…β_k),

где β₁…β_k - параметры регрессионной модели. По количеству факторных переменных регрессионные модели делятся на парные (с одной переменной) и множественные регрессии.

По виду функции f(х, β) регрессионные модели делятся на линейные и нелинейные регрессии.

2. Системы одновременных уравнений, которые описываются системами взаимозависимых регрессионных уравнений.

Системы состоят из тождеств и регрессионных уравнений, каждое из которых может включать в себя как факторные переменные, так и результативные переменные из других уравнений системы. Отличие тождеств от регрессионных уравнений заключается в том, что их вид и значения параметров известны.

Регрессионные уравнения, входящие в состав системы, называются поведенческими уравнениями. Значения параметров этих уравнений являются неизвестными и подлежат оцениванию.

Примером системы одновременных уравнений служит модель спроса и предложения, состоящая из трёх уравнений:

1) уравнения предложения: Q_t^s=a₀+a₁P_t+a₂P_t-1;

2) уравнения спроса: Q_t^d=b₀+b₁P_t+b₂I_t;

3) тождества равновесия: Q_t^s= Q_t^d .

3. Модели временных рядов представляют собой зависимость результативной переменной от переменной времени или переменных, относящихся к другим моментам времени.

Модели временных рядов, в которых результативная переменная зависит от времени:

1) модель тренда (зависимость результативной переменной от трендовой компоненты);

2) модель сезонности (зависимость результативной переменной от сезонной компоненты)

3) модель тренда и сезонности.

Модели временных рядов, в которых результативная переменная зависит от переменных, датированных другими моментами времени:

1) объясняющие вариацию результативной переменной в зависимости от предыдущих значений факторных переменных – модели с распределенным лагом,

2) объясняющие вариацию результативной переменной в зависимости от предыдущих значений результативных переменных - модели авторегрессии;

3) объясняющие вариацию результативной переменной в зависимости от будущих значений факторных или результативных переменных - модели ожидания.

Модели временных рядов могут быть построены по стационарным и нестационарным временным рядам. Для стационарного временного ряда характерны постоянные во времени средняя, дисперсия и автокорреляция.

Этапы эконометрического моделирования.

1. Постановочный этап, на котором определяются конечные цели и задачи исследования, а также число включенных в модель факторных и результативных экономических переменных.

Цели эконометрического исследования:

1) анализ изучаемого экономического процесса (явления, объекта);

2) прогноз экономических показателей, характеризующих изучаемый процесс (явление, объект);

3) моделирование поведения процесса при различных значениях факторных переменных;

4) формирование управленческих решений.

Количество переменных, включенных в эконометрическую модель, не должно быть слишком большим и должно быть теоретически обоснованным, В модели должна отсутствовать функциональная или тесная корреляционная связь между факторными переменными, что может привести к явлению мультиколлинеарности.

2. Априорный этап, на котором осуществляется теоретический анализ сущности изучаемого процесса, а также формализуется априорная информация.

3. Этап параметризации, на котором происходит выбор общего вида модели, а также определяется состав и формы формирующих ее связей.

Задачи, решаемые на этапе параметризации:

1) задача выбора наиболее подходящего вида функциональной зависимости результативной переменной от факторных переменных. При возникновении ситуации выбора между линейной и нелинейной формами зависимости предпочтение всегда отдается линейной форме как более простой;

2) задача спецификации модели:

а) аппроксимация математической формой обнаруженных связей и соотношений между параметрами модели;

б) определение зависимых и независимых переменных;

в) выражение исходных предпосылок и ограничений модели.

4. Информационный этап, на котором собирается требуемая статистическая информация и осуществляется анализ качества собранных данных.

5. Этап идентификации модели, на котором реализуется статистический анализ модели и происходит оценивание ее параметров.

6. Этап оценки качества модели, на котором проверяются достоверность и адекватность модели. Созданная модель должна быть адекватна реальному экономическому процессу. При неудовлетворительном качестве модели возвращаются ко второму этапу моделирования.

7. Этап интерпретации результатов моделирования.

Эконометрическое оценивание моделей. Типы зависимостей и моделей.

Экономическая модель вначале формулируется в общем виде - представляется в виде уравнений, характеризующих связи между экономическими показателями. Например, это может быть одно уравнение, указывающее связь между доходами семей (х) и сбережениями семей (у), величины которых установлены в результате проведенных опросов нескольких сотен случайно отобранных семей:

y = α + βx + ,

где х - объясняющая (независимая) переменная (доходы семей); у - объясняемая (зависимая) переменная (сбережение семей); ε - случайный член (ошибка); α и β - неизвестные наперед, подлежащие определению в результате эконометрического анализа параметры уравнения.

При решении поставленной задачи эконометрики необходимо проверить, соответствует ли эта модель реальным экономическим данным. Различают два уровня анализа: теоретический и эмпирический.

На теоретическом уровне предполагается, что известны все возможные реализации экономических показателей - генеральная совокупность. Зная или предполагая статистические свойства генеральной совокупности, можно теоретически определить параметры модели. На практике чаще всего множество возможных исходов - возможных значений показателей неизвестно, можно наблюдать только выбранные значения интересующих показателей - выборочную совокупность.

На эмпирическом уровне, располагая лишь выборочными значениями экономических показателей - выборочной совокупностью, можно оценить, но нельзя точно определить значения параметров модели. Такие оценки являются случайными величинами. Цель оценивания - получение как можно более точных значений неизвестных параметров модели, характеризующей генеральную совокупность.

В экономических исследованиях одна из основных задач - анализ зависимостей между переменными (показателями). Зависимость может быть функциональной или статистической.

Функциональная зависимость, часто называемая детерминированной, задается в виде формулы, которая каждому значению одной переменной ставит в соответствие строго определенное значение другой переменной (воздействием случайных факторов при этом пренебрегают). В экономике функциональные зависимости между переменными являются исключениями из общего правила.

Статистическая зависимость - это связь переменных, на которую накладывается воздействие случайных факторов. При этом изменение одной переменной приводит к изменению математического ожидания - наиболее вероятного ожидаемого значения другой переменной.

Уравнение регрессии - это формула статистической связи между переменными. Если эта формула линейна, она представляет собой линейную регрессию, а если нелинейная - нелинейную регрессию.

Регрессионный анализ - это процесс определения аналитического выражения функции связи, в котором изменение результативной или зависимой переменной происходит под влиянием факторной, или независимой, переменной. Построение модели парной регрессии позволяет количественно оценить взаимосвязь между результативной и факторной переменными.

Основная модель регрессии - это модель парной, или однофакторной, регрессии, которая называется полиномом первой степени. Модель парной регрессии применяется для характеристики процессов, равномерно развивающихся во времени.

Общий вид модели парной регрессии зависимости переменной у от переменной х:

y_i = β₀ + β₁ x_i + _i,

где y_i - результативные переменные, i=1, 2,...,n; х_i - факторные переменные; β₀, β₁ - неизвестные параметры модели парной регрессии; _i - случайная ошибка регрессионной модели.

Случайная ошибка модели парной регрессии возникает на основе объективных условий, таких как:

1) условие нерепрезентативности выборки, при котором в парную регрессионную модель включается только один фактор, не способный полностью объяснить изменение результативной переменной;

2) условие ошибочного измерения переменных, участвующих в регрессионной модели.

Параметр β₀ в модели парной регрессии - это среднее значение зависимой переменной у при условии, что независимая переменная х равна нулю (если значение х = 0 имеет экономический смысл).

Параметр β₁ в модели парной регрессии - это коэффициент модели регрессии. Значение параметра β₁ характеризует, насколько в среднем изменится зависимае переменная у при изменении факторной переменной х на единицу своего измерение. Знак коэффициента модели регрессии β₁ в модели парной регрессии указывает на направление связи между изучаемыми переменными. Если β₁ > 0, то связь между переменными прямая, т.е. с увеличением переменной х увеличивается и переменная у, и наоборот. Если коэффициент β₁ < 0, то связь между переменными обратная, т.е. с увеличениям переменной х переменная у уменьшается, и наоборот.

Методы определения модели регрессии:

1) метод визуальной оценки характера связи между переменными, при которой на линейном графике по оси абсцисс откладываются значения факторной переменной х, а по оси ординат - значение результативной переменной у. На пересечении соответствующих значений отмечаются точки. Если соединить нанесённые на график точки, то получится эмпирическая линия, по виду которой можно судить не только о наличии, но и о форме зависимости между изучаемыми переменными;

2) метод теоретического и логического анализа природы изучаемых переменных, их социально-экономической сущности.

Точечные оценки: несмещённость, эффективность, состоятельность.

Математическое ожидание - наиболее вероятное ожидаемое значение случайной величины. Математическое ожидание дискретной случайной величины - это сумма произведений всех ее значений на соответствующие им вероятности:

М(х) = ,

где М(х) - математическое ожидание случайной величины х; х_i - i-е значение величины х; p_i - вероятность появления i-го значения величины х; i - порядковый номер дискретного значения величины х; п - общее число дискретных значений величины х.

Математическое ожидание непрерывной случайной величины определяется выражением:

М(х) = _∫xf(x)dx,

где f(х) - плотность распределения величины х, она представляет собой производную функции распределения величины х; ∫ - интеграл, который берётся на всём интервале, в котором определена величина х; dх - дифференциал х.

Случайные величины, с которыми оперируют в эконометрике, имеют нормальное или близкое к нормальному распределение. Математическое ожидание случайной величины (m_x), имеющей нормальное распределение, равно среднему значению генеральной совокупности.

Теоретическая (генеральная) дисперсия случайной величины определяется как математическое ожидание квадрата отклонения случайной величины х относительно ее математического ожидания:

D(x) = M(x – m_x)².

Стандартное отклонение - среднее квадратическое отклонение случайной величины х представляет собой корень квадратный из ее дисперсии:

σ_x =

Стандартное отклонение показывает, насколько в среднем отклоняется случайная величина в совокупности от среднего значения.

Случайные величины, которые используются я эконометрическом анализе, обычно представлены в виде ограниченной выборки. Для нее оценкой математического ожидания служит выборочная средняя - среднее арифметическое значений случайной величины в выборке:

_x = ,

где _x - выборочная средняя; х_i - i-е значение величины х; i - порядковый номер выборочного значения величины х; п - общее число данных в выборке.

Выборочная дисперсия (вариация) представляет собой среднее арифметическое квадратов отклонения случайной величины от среднего значения:

var(x) = .

Стандартное отклонение, т.е. среднее квадратическое отклонение случайной величины х, представляет собой корень квадратный из выборочной дисперсии.

Характеристики генеральной совокупности оценивают на основе характеристик выборочной совокупности - ограниченного числа значений показателей. Характеристики генеральной совокупности принято называть параметрами, а выборочной совокупности - оценками. Чтобы выборочная оценка давала хорошее приближение оцениваемого параметра, она должна удовлетворять требованием несмещённости, эффективности и состоятельности.

Несмещённость оценок. Оценка называется несмещенной, если её математическое ожидание равно оцениваемому параметру при любом объёме выборки. Если это не так, то оценка называется смещённой.

Выборочная средняя является несмещенной оценкой математического _x. ожидания генеральной совокупности - генеральной средней m_х:

m_x =_x .

Выборочная дисперсия var(х) является смещённой оценкой генеральной дисперсии. В качестве несмещённой оценки генеральной дисперсии используется уточненная величина:

где S² - несмещенная оценка дисперсии генеральной совокупности; S – несмещённая оценка стандартного отклонения генеральной совокупности; п - число измерений в выборке; х_i - i-е значение измеренного показателя в выборке: i - порядковый номер измерения.

Величину S обычно называют стандартным отклонением случайной величины в выборке.

Эффективность оценок. Выборочная средняя является эффективной оценкой генеральной средней. Она имеет наименьшую дисперсию в классе несмещённых оценок.

Состоятельность оценок. Оценка называется состоятельной, если при увеличении объёма выборки (n → ∞) она стремится к оцениваемому параметру. Выборочная средняя _x является состоятельной оценкой математического ожидания генеральной совокупности - генеральной средней m_x.

Ковариация. Различают выборочную и теоретическую ковариацию. Выборочной ковариацией двух переменных х и у называется средняя величина произведений отклонений этих переменных от своих средних значений:

где cov(х, у) - ковариация случайных величин х и у; х_i и у_i - i-е значения величин х и y; _x и_y - средние значения величин х и y; i - порядковый номер дискретного значения пар величин х и у; п - общее число дискретных значений пар величин х и y.

Выборочная ковариация служит мерой связи между двумя переменными. Более простое объяснение в качестве меры зависимости между величинами дается с помощью коэффициента корреляции.

Коэффициент корреляции определяется выражением:

где cov(х, у) - ковариация случайных величин х и y; var(х) и var(у) - вариации величин х и y; σ_x и σ_y - стандартные отклонения величин х и y.

Коэффициент корреляции является безразмерной величиной и показывает степень линейной связи двух переменных: r > 0 при положительной связи и r = 1 при строгой положительной линейной связи; r < 0 при отрицательной связи и r = -1 при строгой отрицательной линейной связи; r = 0 при отсутствии линейной связи.

Случайные величины х и у называются некоррелированными, если r = 0, и коррелированными, если r ≠ 0. Если случайные величины х и у независимы, то они и некоррелированы (r = 0), но из некоррелированности не следует их независимость. Некоррелированность указывает лишь на отсутствие линейной связи между переменными.

Для построения модели парной линейной регрессии зависимость между переменными в генеральной совокупности представляется в виде

y = β₀ + β₁ x + ,

где х - объясняющая (независимая) переменная - неслучайная величина; у - объясняемая (зависимая) переменная; ε - случайный член (ошибка регрессии), у и ε - случайные величины; β₀ и β₁ - параметры уравнения.

На основе обработки данных выборочного наблюдения получают уравнение регрессии:

= b₀ + b₁ x + e

где - расчетное значение переменной у; b₀ и b₁ - оценки параметров β₀ и β₁.

Простейшая задача регрессионного анализа состоит в наилучшем представлении набора наблюдений пар величин х и у линейным уравнением регрессии вида

= b₀ + b₁ x

где - расчетное значение переменной у; а и b - оценки параметров α и β.

На рис. 1 приведены диаграмма наблюдений пар величин х и у и график уравнения регрессии - линия регрессии . Эта линия не проходит через точки наблюдений. для каждой точки может быть указано отклонение ее от расчетной величины функции, изображенной линией регрессии:

e_i = y_i - ,

где е_i - отклонение (остаток) i-го наблюдения; у_i - величина переменной у_i в i-м наблюдении; - расчетная величина переменной у в i-м наблюдении, определяемая уравнением регрессии, при значении независимой переменной, равном х_i; i - порядковый номер измерения переменных.

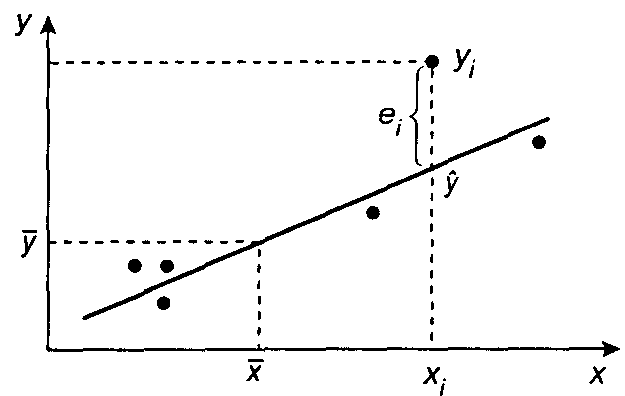
Рис. 1. Точки наблюдений и линия регрессии