8.10.2. Решение задачи об оптимальной диете

с помощью программы MS Excel

Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности предположим, что в качестве исходных типов продуктов рассматриваются хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград (п = 7), в качестве питательных веществ – белки, жиры и углеводы (т = 3). Калорийность одной весовой единицы каждого из продуктов: с₁ = 2060, с₂ = 2430, с₃ = 3600, с₄ = 890, с₅ = 140, с₆ = 230, с₇ = 650. Содержание питательных веществ в каждом из вышеназванных продуктов представлено в табл. 8.12.

Т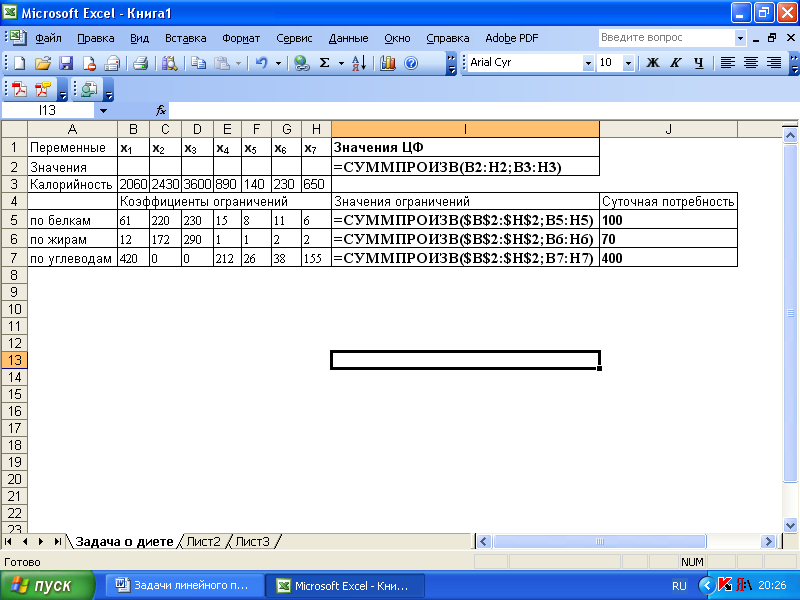 аблица 8.12. Содержание питательных веществ в продуктах питания

Минимальная суточная потребность белков b₁ = 100, жиров b₂ = 70, углеводов b₃ = 400. Калорийность продуктов измеряется в ккал/кг, суточная потребность в питательных веществах – в граммах, а содержание питательных веществ в продукта – в грамм/кг. В этом случае оказывается возможным выполнить дополнительную проверку условий сформулированной задачи на основе рассмотрения физической размерности целевой функции и ограничений. Для решения данной задачи с помощью программы MS Excel создадим новою книгу с именем Линейное программирование и изменим имя ее первого рабочего листа на Задача о диете.

Выполним подготовительные действия:

1. Внесем необходимые надписи в ячейки A1:I1, A2:A7, B4, I4, J4. Конкретное содержание этих надписей не оказывает никакого влияния на решение рассматриваемой задачи линейного программирования.

2. В ячейки В3:Н3 введем значения коэффициентов целевой функции:

с₁ = 2060, с₂= 2430, с₃= 3600, с₄= 890, с₅= 140, с₆= 230, с₇=650.

В ячейку 12 введем формулу =СУММПРОИЗВ(B2:H2;B3:H3), которая представляет целевую функцию.

В ячейки В5:Н7 введем значения коэффициентов ограничений, взятых из табл. 8.12.

В ячейки J5:J7 введем значения правых частей ограничений, соответствующих минимальной суточной потребности в питательных веществах: в белках b₁ = 100, жирах b₂ = 70 и углеводах b₃ = 400; в ячейку I5 введем формулу =суммпроизв($в$2:$н$2;В5:Н5).

Скопируем формулу, введенную в ячейку 15, в ячейки 16 и 17.

Для дальнейшего решения задачи следует вызвать мастер поиска решений, для чего необходимо выполнить операцию главного меню: Сервис|Поиск решения... После появления диалогового окна Поиск решения следует выполнить действия:

1. В поле с именем Установить целевую ячейку ввести абсолютный адрес ячейки $I$2.

2. Для группы Равной выбрать вариант поиска решения, равный минимальному значению.

1. В поле с именем Изменяя ячейки ввести абсолютный адрес $В$2:$Н$2.

2. Добавить 3 ограничения, представляющие минимальные суточные потребности в питательных веществах. С этой целью выполнить действия:

для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить;

в появившемся дополнительном окне выбрать ячейку $I$5, которая должна отобразиться в поле с именем Ссылка на ячейку;

в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство ">=";

в качестве значения правой части ограничения выбрать ячейку $J$5;

для добавления первого ограничения в дополнительном окне на кнопку с надписью Добавить;

аналогичным образом задать оставшиеся два.

5. Добавить ограничение на допустимые значения переменных. С этой целью выполнить действия:

в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить;

в появившемся дополнительном окне выбрать диапазон ячеек $В$2:$Н$2, который должен отобразиться в поле с именем Ссылка на ячейку;

в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство ">=";

в качестве значения правой части ограничения в поле с именем Ограничение ввести значение 0;

для добавления ограничения в дополнительном окне нажать кнопку с надписью Добавить.

6. В дополнительном окне параметров поиска решения следует выбрать отметки Линейная модель и Неотрицательные.

После задания ограничений и целевой функции следует нажать кнопку Выполнить. В результате выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный в табл. 8.13.

Результатом решения задачи об оптимальной диете являются найденные оптимальные значения переменных: Х₁ = 0, Х₂  0,2115, Х₃   0,109, Х₄   1,8868, Х₅ = 0, Х₆ = 0, Х₇ = 0, которым соответствует значение целевой функции f_opt   2587,140389. При выполнении расчетов для ячеек В2:I2 был выбран числовой формат с 4 знаками после запятой.

Таблица 8.13. Результат количественного решения задачи

о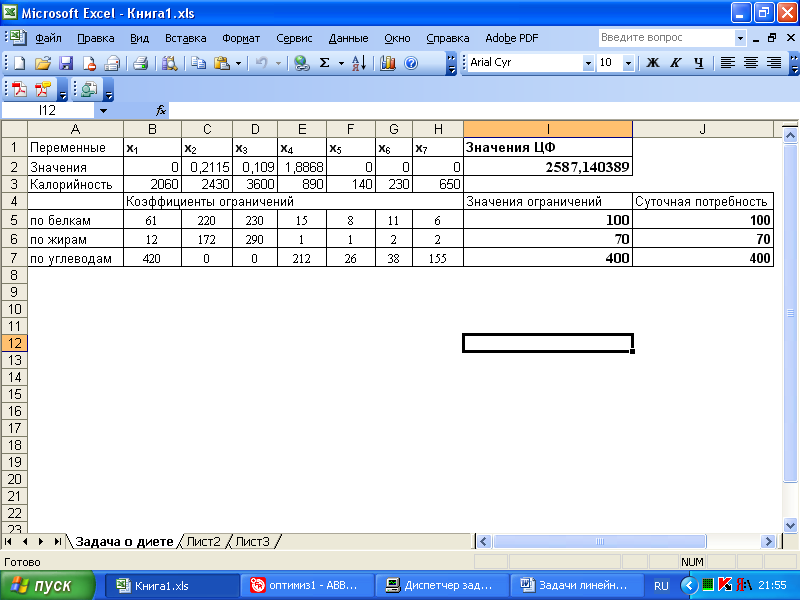 б оптимальной диете

Анализ найденного решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы) следует употреблять 211 г мяса баранины, 109 г сыра и 1887 г бананов, совсем отказавшись от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будет приближенно равна 2590 ккал, что вполне соответствует малоактивному образу жизни без серьезных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников интеллектуального труда (юристы, бухгалтера, врачи, педагоги) лежат в пределах 3000 ккал.