1. Линейные действия над векторами

1. n-мерным вектором называется упорядоченный набор из n вещественных чисел a₁, a₂, …, a_n, называемых координатами или компонентами вектора .

 = (a₁, a₂, …, a_n) – координатная форма записи вектора .

Иногда векторы записываются в виде упорядоченных столбцов (векторы-столбцы): .

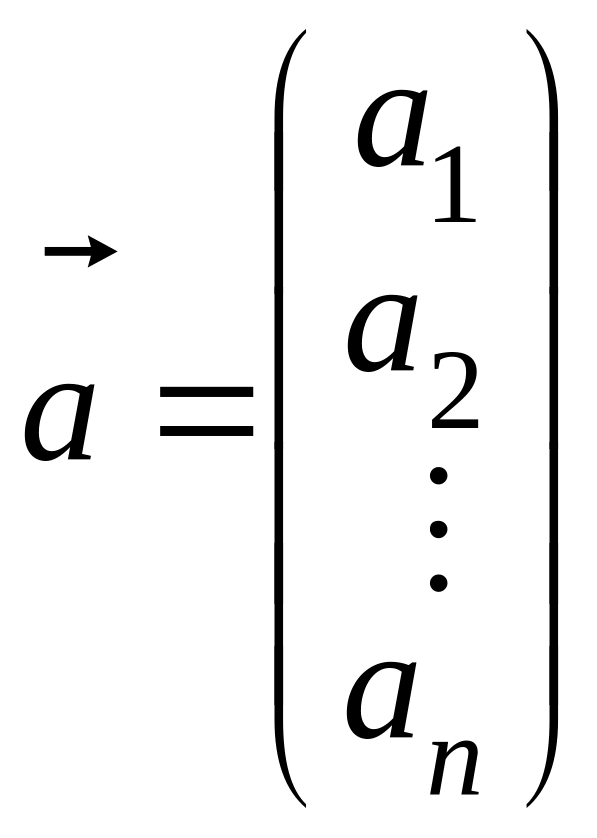Вектор, все координаты которого равны нулю, называется нулевым вектором:  = (0, 0, …, 0). При записи нулевого вектора стрелка часто опускается. Записи и  = 0 – эквивалентны.

Векторы удобно представлять (особенно в двух- и трехмерных пространствах) в виде направленных отрезков. Если А(х₁, х₂, …, х_n) – начало, а В(у₁, у₂, …, у_n) – конец вектора , то  = (y₁ – x₁, y₂ – x₂,…, y_n – x_n).

2. Вектор  = (a₁, a₂, …, a_n) равен вектору  = (b₁, b₂, …, b_n), если a₁ = b₁, a₂ = b₂,…, a_n = b_n. Последнее часто кратко записывают так: a_i = b_i, i =  .

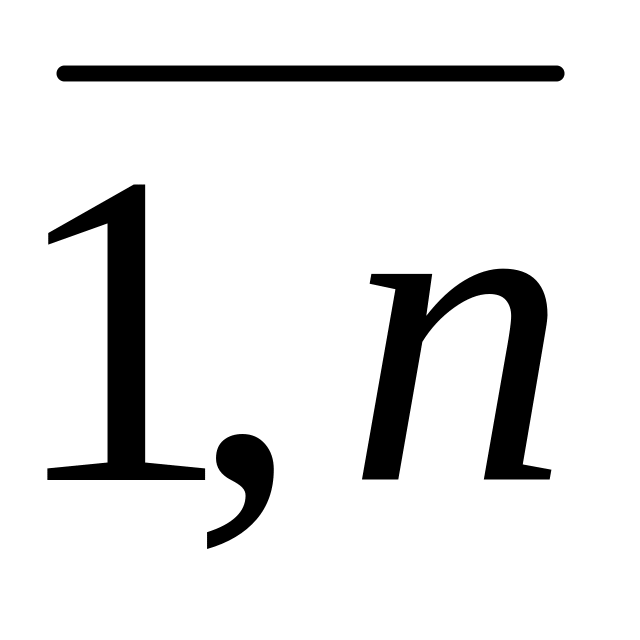3. Произведение вектора  = (a₁, a₂, …, a_n) на скаляр (число) k есть вектор k  = (ka₁, ka₂, …, ka_n). Векторы и k , если , называются коллинеарными. Вектор = (–a₁, –a₂, …, –a_n) называется противоположным вектору .

4. Условие коллинеарности векторов  = (a₁, a₂, …, a_n) и  = (b₁, b₂, …, b_n): .

5. Сумма векторов  = (a₁, a₂, …, a_n) и  = (b₁, b₂, …, b_n) есть вектор  +   = (a₁ + b₁, a₂ + b₂, …, a_n + b_n); разность векторов  и есть вектор  –   = (a₁ – b₁, a₂ – b₂, …, a_n – b_n).

6. Линейной комбинацией векторов ₁, ₂, …, _m называется вектор k_{1 1} + k_{2 2} + …+ k_{m m}; при этом числа k₁, k₂, …, k_m называются коэффициентами линейной комбинации.

7. Векторы ₁, ₂, …, _m называются линейно зависимыми, если хотя бы один из них является линейной комбинацией остальных или, что то же самое, если существуют числа k₁, k₂, …, k_m, среди которых хотя бы одно отлично от нуля, такие, что k_{1 1} + k_{2 2} + …+ k_{m m} = 0.

Векторы ₁, ₂, …, _m называются линейно независимыми, если равенство k_{1 1} + k_{2 2} + …+ k_{m m} = 0 возможно только при k₁ = k₂ = …= k_m = 0 или, что то же самое, если ни один из векторов не является линейной комбинацией остальных.

8. Если А(х₁, у₁, z₁) и В(х₂, у₂, z₂) – концы отрезка АВ, а точка М(х, у, z) делит этот отрезок в отношении , то координаты этой точки:

; ; .

Если М(х, у, z) – середина отрезка АВ, то и

, , .

2. Скалярное произведение векторов

1. Скалярным произведением векторов  = (a₁, a₂, …, a_n) и  = (b₁, b₂, …, b_n) называется число, обозначаемое  или ( , ), равное сумме произведений одноименных координат:

( , ) =    = a₁b₁ + a₂b₂ + … + a_nb_n.

Скалярное произведение векторов обладает следующими свойствами:

( ,  ) = ( ,  );

( + , ) = ( ,  ) + ( ,  );

(k₁ , k₂ ) = k₁k₂( ,  ).

2. Под длиной вектора понимается число, обозначаемое a или , равное: .

3. Расстояние между точками А(a₁, a₂, …, a_n) и В(b₁, b₂, …, b_n) определяется как длина вектора :

.

4. Углом между векторами и называется угол   , косинус которого определяется равенством: .

5. Для скалярного произведения векторов справедливо равенство:

.

6. Векторы и называются ортогональными (перпендикулярными), если .