Коэффициенты косвенных затрат

Косвенные затраты относятся к предшествующим стадиям производства и входят в продукт не непосредственно, а через затраты сопряженных отраслей (рис. 55).

Р ис. 55. Пример формирования косвенных затрат

Коэффициенты косвенных затрат характеризуют количество продукции i–й отрасли, которая направляется в j–ю отрасль для производства единицы ее продукции, проходя k промежуточных стадий.

Коэффициенты косвенных затрат обозначаются , где k – порядок косвенных затрат.

Для определения косвенных затрат первого порядка в матричной форме используют следующую формулу:

А⁽¹⁾ = А  А = А².

Матрица коэффициентов косвенных затрат второго порядка

А⁽²⁾ = А³.

Матрица коэффициентов косвенных затрат k-го порядка

А^(k) = А^k+1. (3.21)

Определим общие (суммарные) косвенные затраты

А^(k) = А² + А³ +… + А^k + … (3.22)

Для получения точной расчетной формулы для суммарных косвенных затрат воспользуемся формулой (3.20):

В = Е + А + А² + … + А^k + … = Е + А + А^(k).

Отсюда получим А^(k) = В – Е – А.

Для автоматизации расчёта задачи межпродуктового баланса возможно использование программы «Межотраслевая балансовая модель В.Леонтьева» из ППП PRIMA.

Исходными данными для расчётов является матрица коэффициентов прямых затрат, вектор известных значений конечного продукта и вектор известных значений валового выпуска (рис. 56).

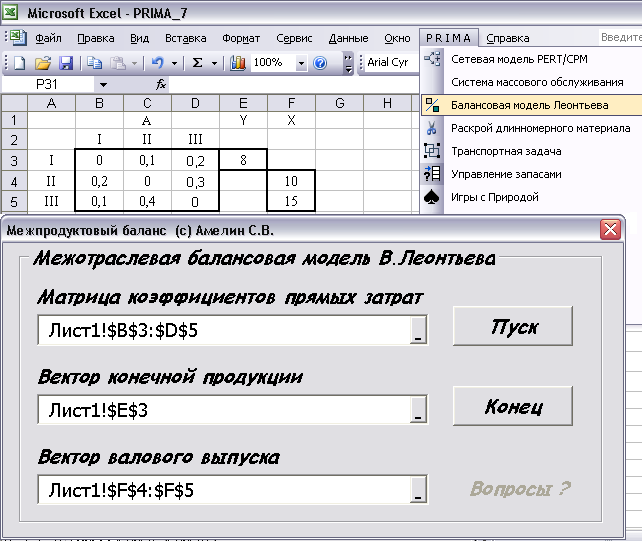
Рис. 56. Ввод исходных данных в диалоговую форму

Результаты расчёта параметров модели межпродуктового баланса представлены на рис. 57.

Рис. 57. Результаты расчёта параметров балансовой модели

Тема 4. Модели линейного программирования

Раздел математических методов, в котором рассматриваются способы решения задач на нахождение экстремума функции цели при ограничении области допустимых значений в форме уравнений или неравенств, называется математическим программированием. Другими словами, математическое (оптимальное) программирование рассматривает задачи планирования, распределения ограниченных ресурсов наилучшим образом, для достижения поставленных целей.

Общая задача математического программирования имеет вид:

определить экстремум функции

f(x)  extremum (max, min),

при выполнении условий

g_i(x) = (, )b_i, (i = ),

x = (x₁, x₂,… x_j …x_n), x_j  0, (j = ),

где f(x) – целевая функция;

g_i(x) - функция ограничения;

b_i - действительное число, константа ограничения.

Если функции f(x) и g_i(x) представлены в виде линейных функций, то оптимизационная задача называется задачей линейного программирования.

Таким образом, линейное программирование – это область математического программирования, посвященная теории и методам решения задач нахождения условного экстремума и характеризующаяся линейной зависимостью между переменными.

Примеры задач линейного программирования

1. Задача планирования производства

Фирма выпускает четыре вида персональных компьютеров

Таблица 4.1

Цех	Затраты времени на единицу продукции, ч				Общий фонд времени, ч/мес
				
Узловой сборки	15	12	4,8	3	480
Сборочный	8,4	4,8	1,8	1,2	252
Испытательный	2,4	1,2	0,12	0,06	90
Доход, ден.ед.	6,5	6	1,5	0,75	__

Определить, сколько изделий и какого вида следует изготовить фирме, чтобы доход за месяц был бы максимальным. Построить экономико-математическую модель задачи.

Решение. Обозначим через х₁ – количество изделий вида , которое должна выпустить фирма; х₂ – количество изделий вида ; х₃ – количество изделий вида ; х₄ – количество изделий вида .

Найдем затраты времени на производственный процесс в цехах (они не должны превышать располагаемый фонд времени)

1 5x₁ + 12x₂ +4,8x₃ + 3x₄  480,

8,4x₁+4,8x₂+1,8x₃ + 1,2x₄  252, (4.1)

2,4x₁ + 1,2x₂ + 0,12x₃ + 0,06x₄  90.

Доход за месяц должен быть максимизирован:

f(x) = 6,5x₁ + 6x₂ + 1,5x₃ + 0,75x₄  max. (4.2)

Выпускается только выгодная продукция (в этом случае х_i > 0), а невыгодная не производится (тогда х_i = 0). Отсюда условие неотрицательности переменных

x₁  0, x₂  0, x₃  0, x₄  0. (4.3)