Отыскание вектора конечной продукции

Для решения второй задачи межотраслевого баланса запишем модель Леонтьева в матричном виде

АХ + Y = Х,

откуда получим выражение (3.9)

Y = (Е – А)  Х.

Пример. Три отрасли выпускают продукцию, причем нормы затрат ресурсов заданы матрицей А, вектор валовой продукции – Х:

А = , Х =

Определить вектор конечной продукции (рис. 54).

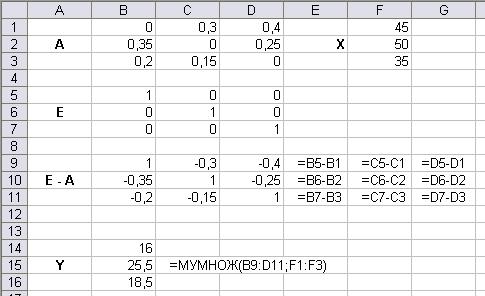
Рис. 54. Расчёт вектора конечной продукции

Смешанная задача межотраслевого баланса

Для решения третьей задачи баланса все отрасли разделим на две группы. К первой группе отнесем отрасли, для которых задан конечный продукт. Множество номеров этих отраслей обозначим индексами i, j = . Ко второй группе отнесем отрасли, для которых задан валовой выпуск. Множество номеров этих отраслей обозначим индексами i, j = . Тогда вектор валовых выпусков можно разделить на два подвектора

Х = , (3.11)

где Х₁ – искомый подвектор с элементами Х_i(i = );

- заданный подвектор с элементами Х_i(i = ).

Аналогично вектор конечного продукта можно разделить на два подвектора

Y = , (3.12)

где – подвектор с известными значениями Y_i(i = );

Y₂ - подвектор с неизвестными значениями

Y_i(i = ).

Матрица А разбивается на четыре подматрицы

А = , (3.13)

где А₁₁ – подматрица с элементами а_ij (i, j = );

А₁₂ – подматрица с элементами а_ij (i = ; j = );

А₂₁ – подматрица с элементами а_ij (i = ; j = );

А₂₂ – подматрица с элементами а_ij (i, j = ).

Для нахождения неизвестных подвекторов Х₁ и Y₂, зная А, , , представим модель Леонтьева в следующем виде:

 + = . (3.14)

Раскроем это выражение

А ₁₁Х₁+А₁₂ + = Х₁ (3.15)

А₂₁Х₁+А₂₂ +Y₂= .

Из первого уравнения этой системы найдем

Х₁ = (Е – А₁₁)^-1  (А₁₂ + ). (3.16)

Из второго уравнения найдем

Y₂ = (Е – А₂₂)  - А₂₁ Х₁ . (3.17)

Найдя из выражения (3.16) Х₁ и подставив в выражение (3.17), получим Y₂.

Пример. Три отрасли выпускают продукцию, причем нормы затрат ресурсов заданы матрицей А:

А = .

Конечный продукт первой отрасли равен 8 ед., объем производства второй отрасли равен 10 ед., а третьей – 15 ед. Определить объем производства первой отрасли и конечный продукт второй и третьей.

Решение. Согласно изложенному ранее первая отрасль входит в первую группу, а вторая и третья – во вторую группу, тогда

Х = , , Y = ,

А₁₁ = (0) А₁₂ = (0,1 0,2)

А₂₁ = А₂₂ = .

Из формулы (16) найдем

Х₁ = (1 - 0)^-1  [(0,1 0,2)  + 8] = 12

Из формулы (3.17) найдем

Y₂ =  -  12 = .

Таким образом, валовой выпуск первой отрасли равен 12 ед., конечный продукт второй и третьей равен 3,1 ед. и 9,8 ед. соответственно.

Коэффициенты полных материальных затрат

Запишем модель в матричной форме

АХ + Y = Х .

Отсюда вектор валовых выпусков

Х = (Е – А)^-1  Y.

Обозначим матрицу (Е – А)^-1 через В, а ее элементы через b_ij (i,j = ). Тогда

Х = В  Y . (3.18)

Коэффициенты полных материальных затрат b_ij показывают общую потребность в продукции i–й отрасли, которая обеспечивает выпуск единицы конечной продукции j–й отрасли.

Для определения матрицы коэффициентов полных материальных затрат существуют две формулы: точная и приближенная.

Формула для точного расчета

В = (Е – А)^-1 . (3.19)

Формула для приближенного расчета получается при разложении матрицы (Е – А)^-1 в ряд Тейлора

В = Е + А + А² + … + А^k + … (3.20)