Хід роботи:

Знайти аналітичні вирази двох головних піддіагоналей і двох бічних піддіагоналей числової спіралі з центром 63.

		7	6	5	4	3	2	1	2	3	4	5	6	7
	VI							VII							VIII
7		219	220	221	222	223	224	225	226	227	228	229	230	231
6		218	173	174	175	176	177	178	179	180	181	182	183	184
5		217	172	135	136	137	138	139	140	141	142	143	144	185
4		216	171	134	105	106	107	108	109	110	111	112	145	186
3		215	170	133	104	83	84	85	86	87	88	113	146	187
2		214	169	132	103	82	69	70	71	72	89	114	147	188
1	V	213	168	131	102	81	68	63	64	73	90	115	148	189	I
2		212	167	130	101	80	67	66	65	74	91	116	149	190
3		211	166	129	100	79	78	77	76	75	92	117	150	191
4		210	165	128	99	98	97	96	95	94	93	118	151	192
5		209	164	127	126	125	124	123	122	121	120	119	152	193
6		208	163	162	161	160	159	158	157	156	155	154	153	194
7		207	206	205	204	203	202	201	200	199	198	197	196	195
	IV							III							II

63 65 75 93

2 10 18

8 8

Будемо розглядати квадратний многочлен: . Для нашого прикладу:

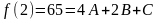
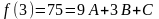
Обчислюємо першу різницю:

R1=(4A+2B+C)-(A+B+C) = 3A+B

R2=(9A+3B+C)-(4A+2B+C) = 5A+B

Обчислюємо другу різницю:

d=(5A+B)-(3A+B)=2A=8

A=8/2=4.

B + C = 63 ­– 4 = 59

2B + C = 65 - 4*4 = 49

B = 49 – 59 = -10; C = 63 – 4 + 10 = 69.

 II

Для даного випадку різниця між двома суміжними діагоналями 2n – 2, де n – індекс стовпчика або рядка для різних випадків.

Тому для знаходження наступнії під діагоналі достатньо додати 2n – 2. Для знаходження підвертикалі достатньо додати половину різниці між піддіагоналями : (2n – 2)/2 = n - 1

Для кожної наступної діагоналі врахуємо зміщення n - 1:

9.  III

10.  I

11.  IV

12.  V

13.  VI

14.  VII

15.  VIII

де n – номер квадрату.

Поділимо матрицю на 4-ри чверті.

Для кожної чверті потрібно використати формулу піддіагоналі, яка знаходиться в цій чверті.

У випадку якщо потрібно знайти елемент матриці [ x, y ] який знаходиться не на основних діагоналях тоді:

1. Визначаємо елемент на діагоналі координати якого відповідають більшій координаті шуканого елемента.

2. Визначаємо різницю t = x – y

3. Значення t додаємо або віднімаємо від елемента, що на діагоналі.

Задання координат в програмі виконується з додатними і від’ємними координатами, таким чином можна отримати в якій чверті знаходиться точка і використати відповідні формули.

Описаний до цього моменту алгоритм працює лише для одного випадку (початку руху на право і за годинниковою стрілкою ).

У випадку руху проти годинникової стрілки потрібно значення Х поміняти на –Х.

На даний момент описано обчислення елемента при русі на право при будь-якому напрямку за годинниковою стрілкою.

Приклад №9