
Міністерство освіти і науки, молоді та спорту України
Національний університет «Львівська політехніка»
Інститут комп’ютерних наук та інформаційних технологій
Кафедра автоматизованих систем управління

Лабораторна роботи №1
на тему:
«Встановлення закономірностей в натуральному ряді»
Львів 2013
Лабораторна робота №1
Тема роботи: Встановлення закономірностей в натуральному ряді
Мета роботи: Навчитись знаходити і аналітично відображати закономірності
розміщення підмножин натурального ряду.
Короткі теоретичні відомості
Додатні числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ..., що з’явилися в результаті рахунку називаються натуральними і утворюють натуральний ряд чисел. Для запису натуральних чисел користуються десятковою системою числення, в основі якої лежать десять знаків - цифр. На першому місці в натуральному ряді стоїть число 1, за ним іде число 2, далі 3 і так до 9. Після 9, згідно з правилом десяткового числення, йде число 10, а за 10 іде 11, і у натуральному ряді немає останнього числа - за кожним натуральним числом стоїть ще одне натуральне число, за яким - ще одне і т.д.
Натуральних чисел нескінченно багато. Найбільше натуральне число назвати в принципі неможливо, оскільки нескінченність ряду таких чисел розуміє обов'язкову наявність числа, більшого будь-якого названого на 1. За цих умов правий край ряду натуральних чисел прийнято позначати символом нескінченності (значок ∞).
Крім того, всяке натуральне число відноситься або до класу простих чисел, або до класу складених чисел; відповідно, ряд натуральних чисел складається з простих і складених чисел. Просте число ділиться без залишку тільки на себе і на 1, тому має лише два позитивних дільники. Натуральне число, яке ділиться без залишку ще на якесь натуральне число, крім самого себе і 1 називається складеним.
Додатково по натуральних числах можна сказати наступне.
Одиниця умовно вважається простим числом, хоча вона не є ні простим, ні складеним числом, адже одиниця має лише один позитивний дільник. Виходить так, що одиниця відповідає критерію простих чисел, бо ділиться на саму себе і на 1, хоча дільник насправді виходить один і той же.
Двійка - той поодинокий випадок, коли в клас простих чисел потрапило парне число. Взагалі ж серед простих чисел більше немає жодного парного числа, оскільки інші парні числа більше 2 діляться як мінімум на 2.
Простих чисел у ряді натуральних чисел теж нескінченна множина в тому сенсі, що прості числа продовжують з'являтися на всьому проміжку ряду натуральних чисел, а не перериваються в якійсь точці ряду.
Прості числа (ті натуральні числа, які мають тільки два натуральних дільники: одиницю й саме себе) зовсім не такі прості, як може здатися на перший погляд. Скоріше навпаки: серед різних чисел вони приховують, напевно, найбільшу кількість загадок, над якими от уже багато сторіч б’ються кращі математики.
Два, три, п’ять, сім, одинадцять, тринадцять, сімнадцять... — щороку математики знаходять усе більші й більші прості числа. Якщо за часів Ейлера таким було 2147483647, то сьогоднішній рекордсмен — 2 у ступені 43112609 мінус 1 — у десятковому записі має 12978189 розрядів! Але математиків набагато більше за конкретні прості числа цікавлять пов’язані з ними закономірності: скільки їх, яка логіка їхньої появи серед натуральних чисел тощо. І якщо нескінченність кількості простих чисел зумів довести ще Евклід, то друге питання математики не можуть розв’язати досі.
Світло на нього кинуло випадкове відкриття польсько-американського математика Станіслава Улама (до речі, наш співвітчизник — він народився в польському тоді Львові). Якось 1963 року, сидячи на нудній доповіді, учений почав за спіраллю заповнювати числами клітинки листка у зошиті, при цьому машинально відзначав серед них прості. Виявилося, що прості числа розташовуються не хаотично, а утворюють орнаменти з діагональних ліній.
Сучасні комп’ютери будують такі «вишиванки» (математики не дуже шанобливо називають їх «скатертинами Улама») для десятків мільйонів чисел, і знайдена закономірність підтверджується. Однак підвести під цю «красу» міцний теоретичний фундамент поки не вдалося.
Прості числа зовсім не такі прості, як може здатися на перший погляд. Скоріше навпаки: серед різних чисел вони приховують, напевно, найбільшу кількість загадок, над якими от уже багато сторіч б’ються кращі математики.
Просте число — це натуральне число, яке має рівно два натуральних дільники (лише 1 і саме число). Решту чисел, окрім одиниці, називають складеними. Таким чином, всі натуральні числа понад одиницю розбивають на прості і складені. Теорія чисел вивчає властивості простих чисел. В теорії кілець простим числам відповідають незвідні елементи.
Натуральних чисел нескінченно багато. Найбільше натуральне число назвати в принципі неможливо, оскільки нескінченність ряду таких чисел розуміє обов'язкову наявність числа, більшого будь-якого названого на 1. За цих умов правий край ряду натуральних чисел прийнято позначати символом нескінченності (значок ∞).
Крім того, всяке натуральне число відноситься або до класу простих чисел, або до класу складених чисел; відповідно, ряд натуральних чисел складається з простих і складених чисел. Просте число ділиться без залишку тільки на себе і на 1, тому має лише два позитивних дільники. Натуральне число, яке ділиться без залишку ще на якесь натуральне число, крім самого себе і 1 називається складеним.
Одиниця умовно вважається простим числом, хоча вона не є ні простим, ні складеним числом, адже одиниця має лише один позитивний дільник. Виходить так, що одиниця відповідає критерію простих чисел, бо ділиться на саму себе і на 1, хоча дільник насправді виходить один і той же.
Двійка - той поодинокий випадок, коли в клас простих чисел потрапило парне число. Взагалі ж серед простих чисел більше немає жодного парного числа, оскільки інші парні числа більше 2 діляться як мінімум на 2.
Простих чисел у ряді натуральних чисел теж нескінченна множина в тому сенсі, що прості числа продовжують з'являтися на всьому проміжку ряду натуральних чисел, а не перериваються в якійсь точці ряду.
Прості числа (ті натуральні числа, які мають тільки два натуральних дільники: одиницю й саме себе) зовсім не такі прості, як може здатися на перший погляд. Скоріше навпаки: серед різних чисел вони приховують, напевно, найбільшу кількість загадок, над якими от уже багато сторіч б’ються кращі математики.
Два, три, п’ять, сім, одинадцять, тринадцять, сімнадцять... — щороку математики знаходять усе більші й більші прості числа. Якщо за часів Ейлера таким було 2147483647, то сьогоднішній рекордсмен — 2 у ступені 43112609 мінус 1 — у десятковому записі має 12978189 розрядів! Але математиків набагато більше за конкретні прості числа цікавлять пов’язані з ними закономірності: скільки їх, яка логіка їхньої появи серед натуральних чисел тощо. І якщо нескінченність кількості простих чисел зумів довести ще Евклід, то друге питання математики не можуть розв’язати досі.
Приклад №1
Хід роботи:
Знайти аналітичні вирази двох головних піддіагоналей і двох бічних піддіагоналей числової спіралі з центром 62.
f2(x) f1(x)
126 |
125 |
124 |
123 |
122 |
121 |
120 |
119 |
118 |
127 |
98 |
97 |
96 |
95 |
94 |
93 |
92 |
117 |
128 |
99 |
78 |
77 |
76 |
75 |
74 |
91 |
116 |
129 |
100 |
79 |
66 |
65 |
64 |
73 |
90 |
115 |
130 |
101 |
80 |
67 |
62 |
63 |
72 |
89 |
114 |
131 |
102 |
81 |
68 |
69 |
70 |
71 |
88 |
113 |
132 |
103 |
82 |
83 |
84 |
85 |
86 |
87 |
112 |
133 |
104 |
105 |
106 |
107 |
108 |
109 |
110 |
111 |
134 |
135 |
136 |
137 |
138 |
139 |
140 |
141 |
142 |
f3(x) f4(x)
Спосіб 1:
Розташувавши числа по спіралі, можна знайти закономірності їх появи на піддіагоналях f1(x), f2(x), f3(x) та f4(x), які можна описати за такими формулами:
f1(x)=
 ;
;
f2(x)=
 ;
;
f3(x)=
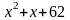 ;
;
f4(x)=
 ;
;
де
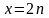 ;
n
;
n
 [0;
[0;
 )–
номер
квадрату (номер числа на будь-якій
піддіагоналі).
)–
номер
квадрату (номер числа на будь-якій
піддіагоналі).
Підставимо в ці формули :
1)
f1(n)= ;
;
2)
f2(n)=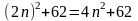 ;
;
3)
f3(n)=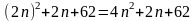 ;
;
4)
f4(n)= ;
;
Між знайденими вище формулами можна знайти ще одну закономірність, і представити її у вигляді такої загальної формули:
fk(n)= ;
де k
[1;4]
– номер
піддіагоналі;
;
де k
[1;4]
– номер
піддіагоналі;
Перевіримо, знайдемо 3-те число у кожній з піддіагоналей:
k=1:
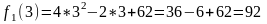
k=2:
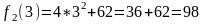
k=3:

k=4:

Спосіб 2:
62 64 74 92 118
2 10 18 26
8 8 8
Будемо
розглядати квадратний многочлен:
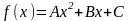 ,
де
x
[1;
).
,
де
x
[1;
).
Для нашого прикладу:

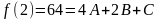

Обчислюємо першу різницю:
R1=(4A+2B+C)-(A+B+C) = 3A+B
R2=(9A+3B+C)-(4A+2B+C) = 5A+B
Обчислюємо другу різницю:
d=(5A+B)-(3A+B)=2A=8
A=8/2=4.
B+C=62-4=58
2B+C=64-4*4=48
B=-10;
C=68.
Аналогічні обчислення робимо і для інших піддіагоналей.
Отже, отримуємо:
1.
f1(x)=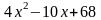
2.
f2(x)=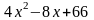
3.
f3(x)=
4.
f4(x)=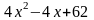
Для перевірки знайдемо п’яте число у кожній з піддіагоналей:
1.
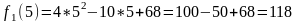
2.
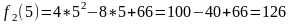
3.
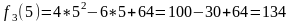
4.

Приклад №2
