2. Ход выполнения работы

Необходимо составить математическую модель для задач лабораторной работы, ввести исходные данные в MS EXCEL и с помощью ПОИСКА РЕШЕНИЯ найти оптимальные значения:

• Установить целевую функцию – создать ссылку на ячейку, в которой записана формула целевой функции, в соответствующих кнопках установить значение, к которому должна стремиться целевая функция – максимальное, минимальное или равное 0:

• Изменяя ячейки – указать те ячейки, в которых находятся изменяемые переменные (что надо определить)

• Ограничения – указать ячейки, в которых записаны ограничения

• Параметры – установить все параметры по умолчанию и добавить:

Линейная модель;

Неотрицательные значения;

Показывать результаты итерации.

• Выполнить – просмотреть по шагам результаты решения

• Вывести отчет по результатам

Рассмотрим пример решения задачи с помощью процедуры Поиск решения.

Пример:

Страховая компания заключает 3 вида страховых договоров по страхованию имущества граждан: страхование автотранспорта, страхование бытовой электроники и страхование предметов искусства и антиквариата. Затраты по каждому из видов страхования представлены в табл. 3. Общая сумма затрат на страхование по всем договорам не должна превышать 20 000 грн.

Таблица 3 – Данные по затратам на 1 договор страхования

Данные о прибыли по каждому договору страхования представлены в табл. 4. Компания намерена развивать только те виды страхования имущества, которые приносили бы максимальную прибыль.

Таблица 4 – Данные по прибыли на 1 договор страхования

Определить, какое количество договоров и по какому виду страхования необходимо заключить компании, чтобы максимизировать свою прибыль.

Решение:

1-й шаг: принимаем за Х переменные, от которых зависит значение целевой функции. Это будут изменяемые ячейки (см. рис. 3).

Рисунок 3 – Создание исходной таблицы для решения задачи

2-й шаг: вводим ограничения, связанные с размером страхового фонда для выплат по договорам страхования.

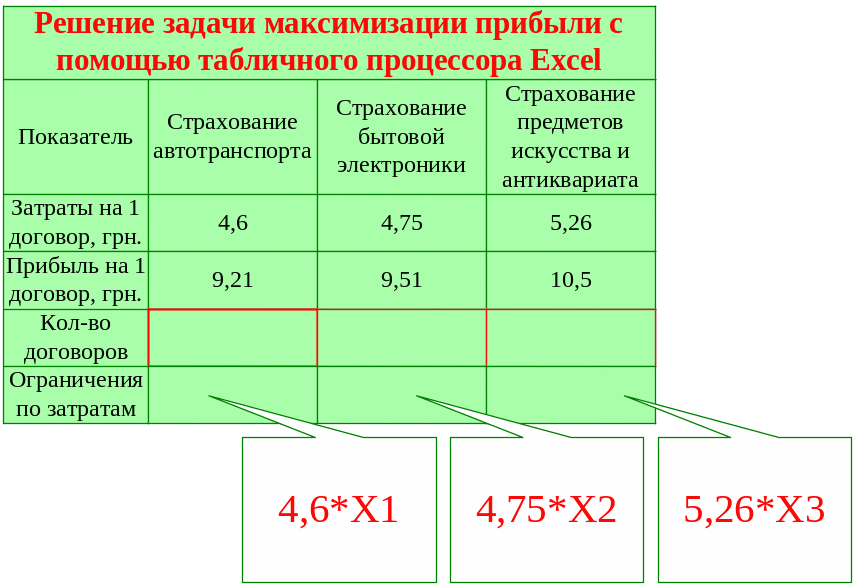
Рисунок 4 – Ввод ограничений задачи в исходные ячейки

3-й шаг: введем в отдельную ячейку функцию ограничений (см. рис.5)

Рисунок 5 – Ввод функции ограничений задачи в отдельную ячейку

4-й шаг: записываем в отдельную ячейку целевую функцию (см. рис. 6)

9,21*Х1+9,51*Х2+10,5*Х3 → max

Рисунок 6 – Ввод целевой функции

Щелчком мыши необходимо сделать ячейку, содержащую формулу, активной и выбрать в меню Сервис команду Поиск решения.

5-й шаг: заполним диалоговое окно надстройки Поиск решения (см. рис.7)

Рисунок 7 – Заполнение надстройки Поиск решения для решения задачи

Поскольку активна ячейка, содержащая целевую функцию, то в поле Установить целевую ячейку будет находится ссылка на нее. Если активной была бы не ячейка с формулой, а какая-то другая ячейка, необходимо было бы в этом поле задать ссылку на целевую ячейку.

Щелчком на одном из трех переключателей задать цель оптимизации ( в данном случае – максимальному значению). Далее щелчком мыши или нажатием клавиши Tab перейти в поле Изменяя ячейки и задать там ссылку на ячейки, содержащие переменные решаемой задачи. Проще всего задать эти ссылки, выделив нужные ячейки.

Щелчком на кнопке Добавить открыть окно Добавление ограничения. В открывшееся поле необходимо ввести ссылки на ячейки, содержащие ограничения и в раскрывающемся списке выбрать знак операции сравнения или условие целочисленности.

Щелчком мыши на кнопке Параметры необходимо задать параметры решения задачи. Тип задачи - линейная, значения – неотрицательные. Затем щелкнуть в окне Поиск решения по кнопке Выполнить.

6-й шаг: результаты, полученные после выполнения процедуры Поиск решения (см. рис. 8)

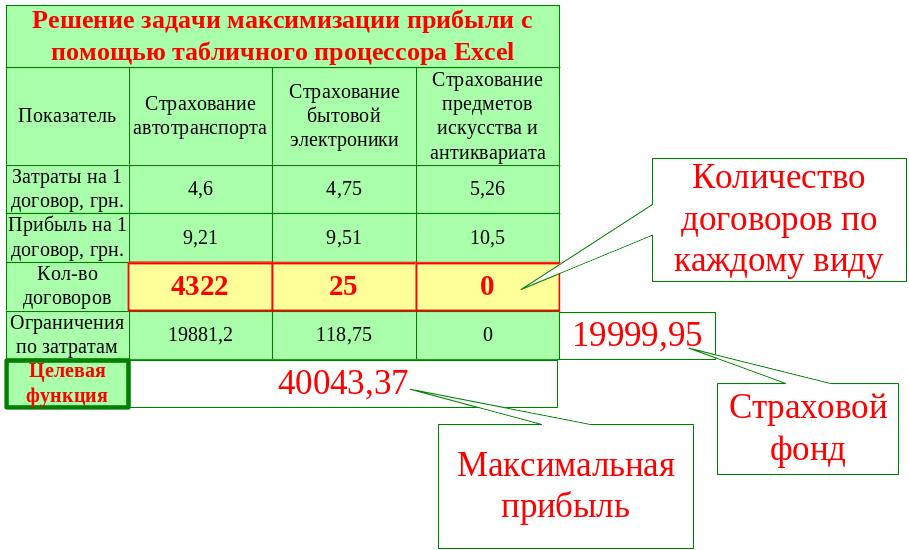Рисунок 8 – Результаты решения задачи

Одновременно с перечетом таблицы раскроется окно Результаты поиска решения. Если необходимо сохранить исходные данные (начальный сценарий) и результаты на отдельном рабочем листе, следует в списке Тип отчета выбрать Результаты, затем щелкнуть на кнопке Сохранить сценарий и задать в открывшемся окне имя этого сценария. При этом в рабочую книгу добавится лист Отчет по результатам 1. Этот отчет содержит полную информацию об исходных данных, ограничениях и итогах вычислений. Так можно сохранить информацию о решении задачи при разных условиях, а затем сравнить эти варианты.

По умолчанию в диалоговом окне Результаты поиска решения включен переключатель Сохранить найденное решение. Если ничего не меня, щелкнуть на кнопке ОК, полученные результаты вычислений будут сохранены. А если включить переключатель Восстановить исходные значения и щелкнуть на кнопке ОК, восстановится исходная расчетная таблица.

Таким образом, страховой компании для получения максимальной прибыли в сумме 400043,37 грн. следует заключить 4322 договора по страхованию автотранспорта, 25 договор страхования бытовой электроники и не заключать договоров страхования предметов искусства и антиквариата.

Задачи для решения:

Задача №1

Определить максимальную прибыль, которая может быть получена при изготовлении трех видов изделия: телевизоров, стереосистем и аудиосистем, в каждом из этих изделий используются комплектующие: шасси, кинескоп, динамик, блок питания, электрическая плата. На складе находится: 450 шасси, 250 кинескопов, 800 динамиков, 450 блоков питания, 800 электрических плат. Количество используемых комплектующих в готовых изделиях и прибыль с 1 единицы изделия показано в табл. 5.

Таблица 5 – Исходные данные

Комплектующие	Изделия
	Телевизоры	Стереосистемы	Ак. системы
Шасси	1	1	0
Кинескопы	1	0	0
Динамики	2	2	1
Бл. питания	1	1	0
Элект. платы	2	1	1
Прибыль с 1 ед. изделия	300	220	100

Задача № 2

Определить количество выпускаемых изделий А, Б, В, если затраты на приобретение комплектующих для изготовления этих изделий не должны превышать 1000 ден. ед. Количество комплектующих в каждом из изделий, минимальная потребность в изделиях и цена за 1 ед. комплектующих представлены в табл. 6.

Таблица 6 – Исходные данные для решения задачи

	Комплектующие		Минимальная потребность в изделиях
	№1	№2
Изделие А	1	1	4
Изделие Б	1	2	6
Изделие В	1	0	1
Цена за 1 ед.комплектующих	6	3

Задача № 3

Вы являетесь логистом сети магазинов «Велiка кiшеня». На складах С1, С2 и С3 имеются запасы овощей в количестве 90 т, 400 т и 110 т соответственно. Магазин «Муссон» ежедневно требует поставки 140 т, магазин «Фуршет» - 300 т, магазин «Клондайк» - 160 т. Необходимо найти такой вариант перевозок, при котором сумма затрат на транспортировку овощей была бы минимальной. Расходы на перевозку 1 т овощей представлены в табл. 7.

Таблица 7 – Данные по затратам на перевозку, грн.

Склады	Супермаркет "Муссон", грн.	Супермаркет "Фуршет", грн.	Супермаркет "Клондайк", грн.
С1	2	5	2
С2	4	1	5
С3	3	6	8

Задача № 4

Банк «Финасист» размещает имеющиеся ресурсы в сумме 4 600 000 грн. в доходные активы (кредиты). При этом банк кредитует проекты сроком на 1 месяц и на 3 месяца. Процентная ставка по кредиту сроком 1 месяц составляет 5 % в месяц, а по кредиту сроком на 3 месяца - 14,9 %. Данные по затратам банка на обслуживание кредитов: 3 % от величины 1-месячного кредита и 2,9 % от величины 3-месячного кредита. При этом затраты банка на обслуживание кредитов не должны превышать 45 000 грн в 1-й месяц, 40 000 грн. во 2-й месяц, 32 000 грн. в 3-й месяц. Затраты банк несет по каждому кредиту ежемесячно. Определить оптимальную величину кредитов, чтобы доход банка был максимальным.

Таблица 8 – Форма для составления оптимального плана удовлетворения кредитных заявок

Месяц	1-й месяц	2-й месяц	3-й месяц	4-й месяц
Свободные средства	4600000
Возвращение кредита
Проценты по кредиту, полученные банком
Сумма кредита сроком 1 месяц
Сумма кредита сроком 3 месяца
Затраты
Конечная сумма

Задача № 5

Фирма «Союз» рассматривает возможность финансирования нескольких инновационных проектов со следующими данными:

Проекты	Затраты , грн.	Чистая текущая стоимость, грн.
Проект «Вепрь»	180000	125000
Проект «Тигр»	160000	119000
Проект «Барс»	170000	154000
Проект «Пума»	110000	145000
Проект «Фламинго»	140000	126000
Проект «Крот»	110000	128000

Необходимо выбрать пакет инвестиций, которые принесли бы максимальную прибыль, если бюджет фирмы составляет 600000 грн.

Задача № 6

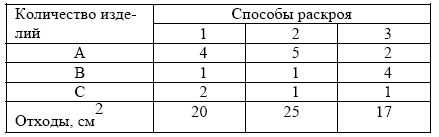
Изделия трех видов (А, B, C) вырезаются из стальных листов. Предприятие имеет 150 стальных листов. Каждый лист можно раскроить одним из трех способов. Количество изделий, получаемых из одного листа, и величины отходов для каждого способа раскроя приведены в табл.9.

Предприятию необходимо раскроить листы таким образом, чтобы отходы были минимальны. При этом необходимо выпустить не менее 400 изделий A, не менее 250 изделий B и не более 300 изделий C (последнее требование связано с тем, что спрос на изделия C ограничен).

Таблица 9 – Исходные данные

Задачи для СРС:

Задача №1

Один из цехов кондитерской фабрики выпускает шоколадные изделия двух видов: плитки шоколадные «Аленка» и плитки шоколадные «Цыганка». Для производства этих изделий требуются 3 вида сырья: какао-бобы, молоко, сахар. На выпуск одной шоколадки «Аленка» расходуется 200 г какао-бобов, 100 г молока и 50 г сахара. На выпуск одной шоколадки «Цыганка» расходуемся 50 г какао-бобов, 50 г молока и 20 г сахара. Запасы ресурсов ограничены: за рабочую смену цех может израсходовать не более 2000 г какао-бобов, 2500 г молока и 5000 г сахара.

Выпуск одной шоколадки «Аленка» приносит предприятию прибыль в размере 1 грн., одной шоколадки «Цыганка» - 3 грн. Требуется составить оптимальный план работы цеха, т. е. найти, сколько шоколада «Аленка» и «Цыганка» требуется выпускать, чтобы получить максимальную прибыль (при соблюдении ограничений на ресурсы).

Задача №2

С двух складов гипермаркета «Ален» (Ск1 и Ск2) поставляется рыба в супермаркет «Ахтиар», супермаркет «Кардинал» и супермаркет «Океан». На складе 1 (Ск1) хранится 60 т рыбы, на складе 2 (Ск2) – 35 т рыбы. Потребности супермаркета «Ахтиар»– 40 т рыбы, супермаркета «Кардинал» – 25 т рыбы, супермаркета «Океан» – 30 т рыбы. Затраты на перевозку рыбы представлены в таблице. Необходимо составить план перевозок, при котором затраты на перевозку будут минимальны.

Таблица 10 – Данные по затратам на перевозку, грн.

Склады	Супермаркеты
	«Ахтиар	«Кардинал»	«Океан»
Склад 1 (Ск1)	15	25	12
Склад 2 (Ск2)	9	10	8

Задача №3

Компания «EuroМoney» располагает свободными денежными средствами в сумме 48000 грн., которые хочет выгодно вложить. Банк «Finance» предлагает компании размещение средств в депозиты сроком на 1 месяц и 2 месяца. Ставка по 1-месячному депозиту составляет 3 % в месяц, а по 2-месячному – 6 % за 2 месяца. Ежемесячные данные по затратам на размещение депозита представлены в таблице. Необходимо определить оптимальную величину депозитов, чтобы прибыль, полученная от размещения денежных средств, была максимальной. При этом в распоряжении компании должно оставаться не менее 5000 грн. каждый месяц.

Таблица 11 - Форма для составления оптимального плана размещения депозитных вкладов

Месяц	1-й месяц	2-й месяц	3-й месяц	4-й месяц	5-й месяц
Свободные средства, грн.	48000
Возвращение депозита, грн.
Проценты полученные, грн.
Сумма депозита сроком 1 месяц, грн.
Сумма депозита сроком 2 месяца, грн.
Затраты, грн.	3600	4800	5600	4200
Конечная сумма, грн.

Задача №4

Рассчитать оптимальный запас товара, отпускаемого со склада по цене 120 грн. за единицу, цена приобретения товара у поставщика составляет 100 грн. за единицу, издержки хранения всей партии товара на складе составляют 600 грн. По имеющимся данным минимальный запас должен быть не менее 200 единиц товара, но в связи с малой площадью склада не может превышать 1000 единиц. Определить оптимальный запас товара, при котором доход фирмы был бы максимален, если бюджет фирмы не превышает 50000 грн., а удельный доход фирмы на единицу товара не превышает 18 грн.

Контрольные вопросы:

1. Что называется линейной математической моделью? Приведите примеры экономических и финансовых задач, для решения которых необходимо составить линейную математическую модель.

2. Чем отличается оптимальное решение модели от допустимого?

3. Что представляют собой задачи безусловной и условной оптимизации?

4. Перечислите типовые задачи линейного программирования.

5. Каковы особенности транспортных задач?

6. Что такое целевая функция, изменяемые ячейки и ограничения?

7. Когда лучше применять модель Ньютона, а когда – сопряженных градиентов?

8. Что задает параметр Сходимость?