М
инистерство
образования и науки Украины
Севастопольский национальный технический университет
Методические указания
к выполнению лабораторных работ
по дисциплине
«Информационные системы
в финансово-кредитных учреждениях»
студентов специальности 7.050104 «Финансы»
дневной формы обучения
Севастополь
2007
УДК 336.11
Методические указания к выполнению курсовой работы по дисциплине «Информационные системы в финансово-кредитных учреждениях» / Сост. ст преп. Н. А. Глухова, асс. Д. В. Черемисинова. – Севастополь: Изд-во СевНТУ, 2007. - 64 с.
Цель методических указаний состоит в оказании необходимой методической помощи студентам в качественном выполнении лабораторных работ по дисциплине “Информационные системы в финансово-кредитных учреждениях”.
Методические указания предназначены для студентов и преподавателей кафедры «Финансы и кредит».
Методические указания рассмотрены и утверждены на заседании кафедры “Финансы и кредит” (протокол №12 от 12.03.2007 г.)
Допущено научно-методическим центром СевНТУ в качестве методических указаний.
Рецензент:
к.т.н., доцент кафедры «Учет и аудит» Шепилов К. Ю.
Содержание
Введение |
4 |
Лабораторная работа №1 «Использование надстроек табличного процессора Excel для решения задач оптимизации |
5 |
Лабораторная работа №2 «Реализация задач корреляционно-регрессионного анализа с помощью табличного процессора Excel» |
23 |
Лабораторная работа №3 «Имитационное моделирование денежных потоков инвестиционного проекта в среде EXCEL |
39 |
Библиография |
64 |
Введение
Лабораторные работы по дисциплине “Информационные системы в финансово-кредитных учреждениях” являются одной из форм работы студентов и выполняются в соответствии с образовательной программой подготовки бакалавров экономики по специальности “Финансы”.
Данные методические указания содержат три лабораторные работы, в которых дается описание применения основных функций табличного процессора Excel при решении задач экономического и финансового характера. В лабораторных работах приведены формулировки задач, предназначенных для решения в электронных таблицах MS Excel. Вспомогательные рисунки, таблицы, примеры диаграмм и графиков способствуют четкому восприятию материала и пониманию вида выходной информации. Разнообразные задания сочетают работу с данными, использование одной или нескольких функций, обработку числовой и нечисловой информации, построение диаграмм.
При выполнении лабораторных работ студент должен применить теоретические знания, полученные на лекциях для решения практических задач в различных информационных системах.
Задача данных методических указаний состоит в оказании необходимой методической помощи студентам в качественном выполнении лабораторных работ.
Методические указания определяют цель и порядок выполнения лабораторных работ и способ оформления отчета.
Лабораторная работа №1 «Использование надстроек табличного процессора Excel для решения задач оптимизации»
Цель работы: освоение процедур математического моделирования и оптимизации решений в задачах экономического прогнозирования, планирования, диагностики и управления с использованием табличного процессора Excel
1. Теоретическая часть
При решении конкретной задачи оптимизации в экономике исследователь прежде всего должен выбрать математический метод, который приводил бы к конечным результатам с наименьшими затратами на вычисления или же давал возможность получить наибольший объем информации об искомом решении. Выбор того или иного метода в значительной степени определяется постановкой оптимальной задачи, а также используемой математической моделью объекта оптимизации. В данной лабораторной работе будут рассмотрены такие примеры экономических задач, как минимизация затрат, максимизация прибыли и оптимального размещения ресурсов при наличии ряда ограничений. Эти задачи предполагают использование метода линейного программирования.
Под линейным программированием понимается раздел теории экстремальных задач, в котором изучаются задач и минимизации (или максимизации) линейных функций на множествах, задаваемых системами линейных равенств и неравенств.
Линейная математическая модель – модель задачи, в которой требуется найти такие значения переменных Х1, Х2, …, Хn, при которых некоторая линейная функция от этих переменных принимает максимальное (max) или минимальное (min) значение.
Такая линейная функция называется целевой функцией.
F(X) = C1X1+C2 X2 +…+CnXn→ max
или
F(X) = C1X1+C2 X2 +…+CnXn→ min
при выполнении ограничений на переменные Х1, Х2, …, Хn. Ограничения задаются в виде уравнений или неравенств:
А11Х1+А12Х2+…+А1nXn ≥ ≤ B1
А21Х1+А22Х2+…+А2nXn ≥ ≤ B2
……………………………………..
Аp1Х1+Аp2Х2+…+АpnXn ≥ ≤ Bp
Допустимые решения модели – любые значения переменных Х1, Х2, …, Хn, удовлетворяющие ограничениям задачи.
Оптимальное решение модели – допустимые значения переменных Х1, Х2, …, Хn, при которых целевая функция принимает максимальное или минимальное значение.
Математический аппарат линейного программирования специально создан для решения задач с линейными критериями оптимальности и линейными ограничениями на переменные и позволяет решать большинство задач, сформулированных в такой постановке.
В зависимости от области определения целевой функции различают задачи условной и безусловной оптимизации. К задачам безусловной оптимизации относятся те, в которых экстремумы ищутся без ограничения влияющих параметров. Однако в экономике всегда присутствуют те или иные ограничения. Поэтому большинство реальных задач относится к числу задач условной оптимизации, а найденные при этом экстремумы называются условными.
Для решения большого круга задач линейного программирования имеется практически универсальный алгоритм - симплексный метод, позволяющий за конечное число итераций находить оптимальное решение подавляющего большинства задач. Тип используемых ограничений (равенства или неравенства) не сказывается на возможности применения указанного алгоритма. Дополнительной проверки на оптимальность для получаемых решений не требуется. Как правило, практические задачи линейного программирования отличаются весьма значительным числом независимых переменных. Поэтому для их решения обычно используют вычислительные машины, необходимая мощность которых определяется размерностью решаемой задачи.
Типовые задачи линейного программирования:
1) «задача о раскрое» - как с наименьшими отходами использовать материал при производстве заданного количества изделий;
2) «задача о смесях» (еще одно название данного типа задач – «задача о рационе») – определение такого рациона, который удовлетворял бы потребностям человека или животного в питательных веществах или минимальной общей стоимости используемых продуктов;
3) «задача о назначениях» - каким образом распределить рабочих по станкам для получения максимальной прибыли от производства;
4) задача об определении оптимального ассортимента – найти такую структуру выпускаемой продукции, чтобы получать максимальную прибыль;
5) транспортная задача – найти такой оптимальный план перевозок, чтобы все заявки были удовлетворены при минимальных затратах на перевозку;
6) построение оптимального портфеля ценных бумаг – получение максимального дохода от вложений в ценные бумаги при минимальном риске.
Отдельный распространенный тип задач линейного программирования представляют транспортные задачи. Эти задачи, как и любые задачи линейного программирования, могут решаться с использованием симплекс-метода. Однако для решения транспортных задач существуют специальные, более простые методы.
Общая постановка транспортной задачи следующая. Имеются M поставщиков некоторого товара. Количество товара, имеющееся у поставщиков, составляет A1, A2, ..., AM единиц. Имеются N потребителей этого товара; их спрос составляет B1, B2, ..., BN единиц. Сумма запасов товара, имеющихся у поставщиков, равна сумме величин спроса всех потребителей:
Известны затраты на перевозку единицы товара от каждого поставщика каждому потребителю (стоимости перевозок): Cij, i = 1, ..., M,
j = 1, ..., N. Требуется составить оптимальный план перевозок, т.е. определить, сколько товара каждый поставщик должен доставлять каждому из потребителей, чтобы общие затраты на перевозки были минимальными. При этом, конечно, каждому потребителю должно быть доставлено необходимое количество товара.
Рассмотрим пример построения линейной математической модели для решения транспортной задачи.
Пример.
С четырех складов (СК1, СК2, СК3, СК4) доставляется товар в три магазина (МГ1, МГ2, МГ3). На складе СК1 имеется 40 тонн товара, на складе СК2 – 50 тонн, на складе СК3 – 60 тонн, на складе СК4 – 30 тонн. Магазину МГ1 требуется 60 тонн товара, магазину МГ2 – 80 тонн, магазину МГ3 – 40 тонн. Затраты (в ден. ед.), связанные с перевозкой одной тонны товара с каждого склада в каждый магазин, приведены в табл. 1.
Таблица 1 – Данные по затратам на перевозку, ден. ед.
Требуется определить, сколько товара необходимо перевезти с каждого склада в каждый магазин, чтобы доставить всем магазинам необходимое количество товара с минимальными затратами.
Решение:
Данную задачу можно представить как задачу линейного программирования. Для построения математической модели этой задачи введем переменные Xij, i = 1, ..., 4, j = 1, ..., 3, обозначающие количество товара, перевозимого с i-го склада в j-й магазин.
На складах имеется 180 единиц товара; магазинам требуется также 180 единиц товара. Поэтому для удовлетворения спроса всех магазинов потребуется вывезти со складов весь товар. Ограничения, выражающие это требование, имеют следующий вид:
X11 + X12 + X13 = 40
X21 + X22 + X23 = 50
X31 + X32 + X33 = 60
X41 + X42 + X43 = 30.
Каждый магазин должен получить ровно столько товара, сколько ему
требуется. Ограничения, выражающие это условие, следующие:
X11 + X21 + X31 + X41 = 60
X12 + X22 + X32 + X42 = 80
X13 + X23 + X33 + X43 = 40.
Так как переменные обозначают количество перевозимого товара, на них накладывается требование неотрицательности:
Xij ≥ 0, i= 1, ..., 4, j = 1, ..., 3.
Целевая функция представляет собой затраты на выполнение всех перевозок:
E = 4X11 + 3X12 + 5X13 + 6X21 + 2X22 + 1X23 + 10X31 +4X32 +7X33 + 8X41 + 6X42 + 3X43 → min.
При решении транспортной задачи удобно пользоваться расчетной таблицей, содержащей стоимости перевозок, запасы товара у поставщиков и величины спроса потребителей. По ходу решения задачи в нее заносятся
величины перевозок (значения переменных Xij), а также вспомогательные величины, используемые для решения задачи. Расчетная таблица для данного примера показана в табл. 2.
Таблица 2 – Расчетная таблица для решения транспортной задачи
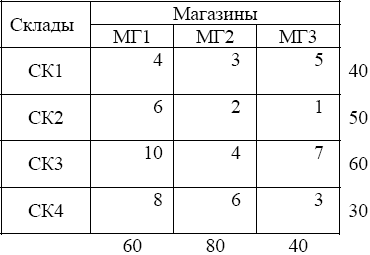
Решение транспортной задачи включает два этапа:
• поиск допустимого решения, т.е. плана перевозок, при котором каждый потребитель получит весь необходимый товар, однако затраты на такие перевозки могут не быть минимальными;
• поиск оптимального решения, т.е. плана перевозок с минимальными
затратами.