3.2.4 Двигатель постоянного тока

1. Уравнения статики для номинального режима имеют вид

,

,

где – коэффициент противо - ЭДС якоря, – коэффициент вращающего момента. При единице измерения рад/с в системе единиц СИ выполняется равенство с размерностью [7, с.25]. Тем самым найдем

, .

Например, для двигателя №1 получим

, .

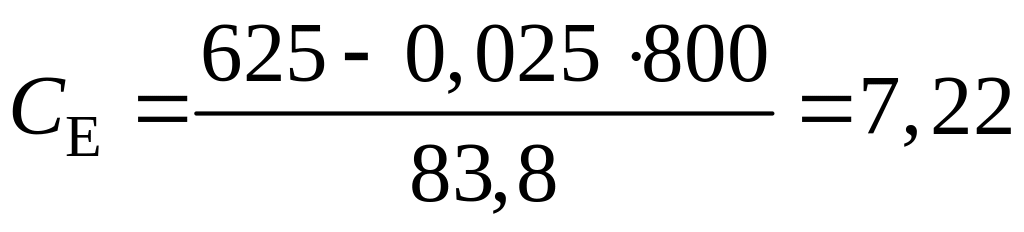
2. Уравнения динамики двигателя в схеме соединения имеют вид

,

,

где , ; при этом – для схем А, Б; – момент нагрузки приведенный к валу двигателя для схем Г, Д.

Отсюда с учетом преобразования Лапласа при нулевых начальных условиях найдем:

,

где , , , , .

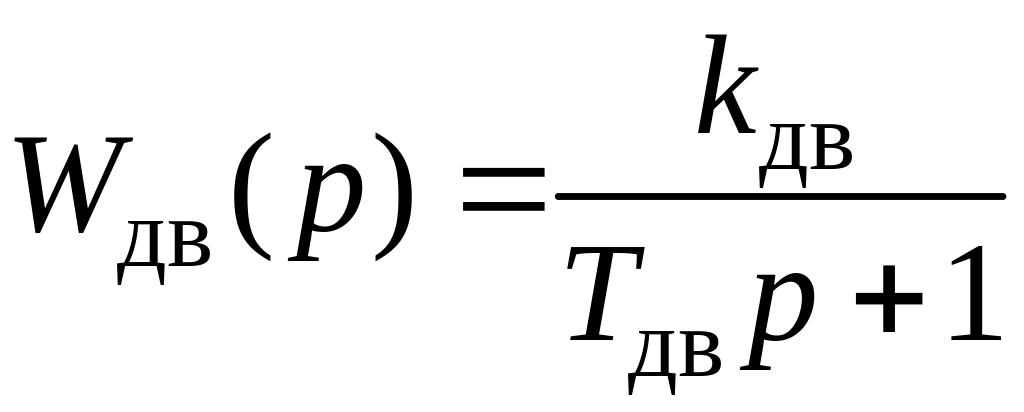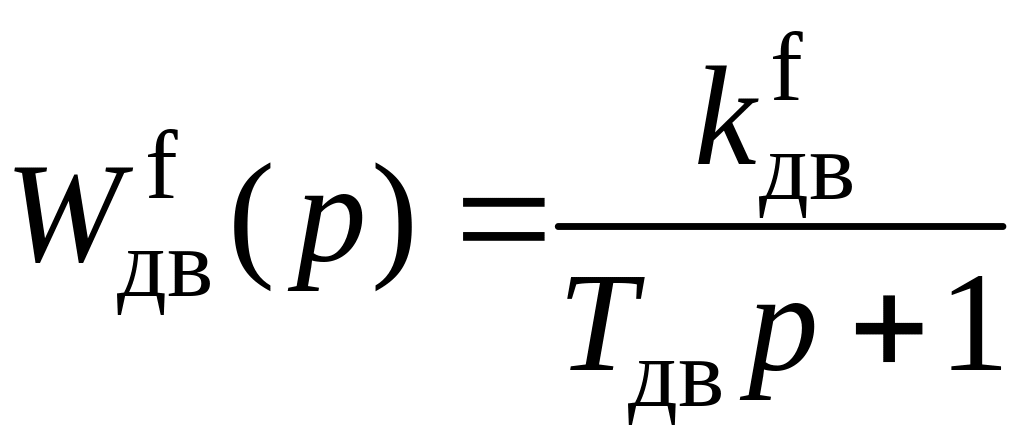Для схем Г, Д выходной координатой двигателя является угол поворота ротора , т.е. и, следовательно,

,

где , .

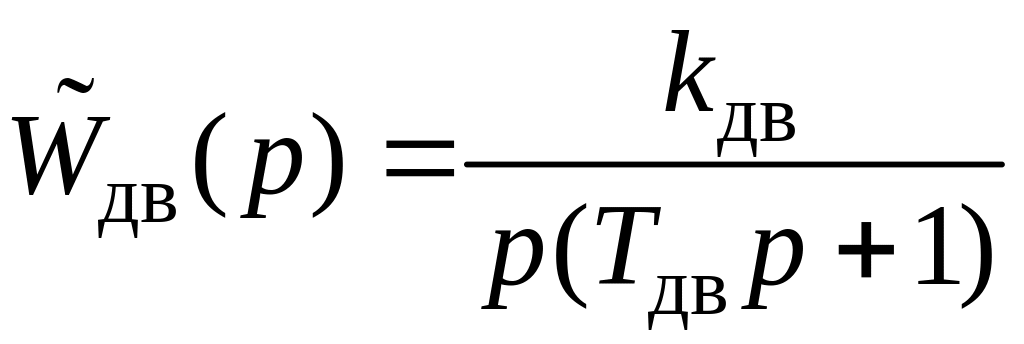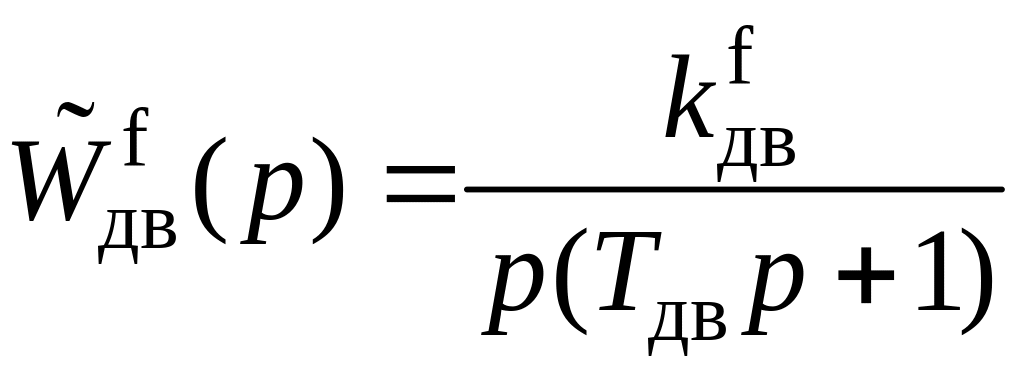Например, для двигателя и генератора №1 получим

,

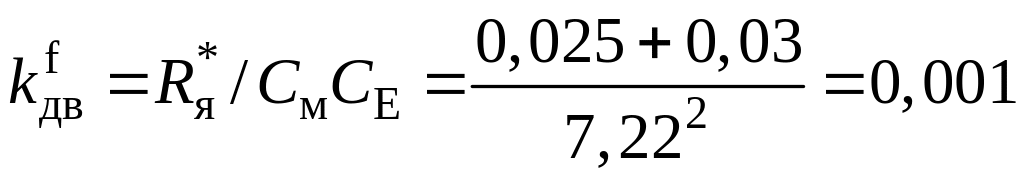
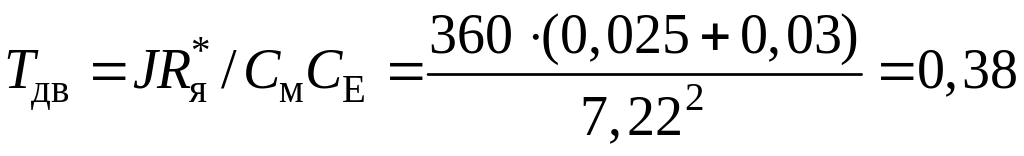с.

3.3 Определение передаточных функций замкнутых систем

При определении передаточных функций замкнутых систем следует использовать передаточные функции разомкнутых систем. Для этого можно использовать следующее правило для структурных схем с одним контуром обратной связи:

в числителе передаточной функции указывается произведение передаточных функций с учетом знаков, через которые проходит входной сигнал до заданного выходного сигнала кротчайшим путем; в знаменателе передаточной функции указывается выражение , где – передаточная функция разомкнутой системы, равная произведению передаточных функций от сигнала рассогласования до сигнала главной отрицательной обратной связи, поступающего на устройство сравнения.

В качестве примера рассмотрим структурную схему системы для схемы Д, представленную на рис. 14. Данная схема содержит два контура: контур отрицательной местной обратной связи по сигналу и контур отрицательной главной обратной связи по сигналу . Приведенное правило используется для каждого контура.

Найдем, например, зависимость , т.е. определим передаточные функции , .

а) Выпишем выражение для передаточной функции , для этого установим путь сигнала до сигнала , который проходит через устройство сравнения с коэффициентом передачи равным единице. Следовательно, числителем передаточной функции является единица. При определении передаточной функции разомкнутой системы сигнал проходит через контур с местной обратной связью, для которого в свою очередь зависимость выхода от входа через передаточную функцию согласно правилу определяется по формуле

.

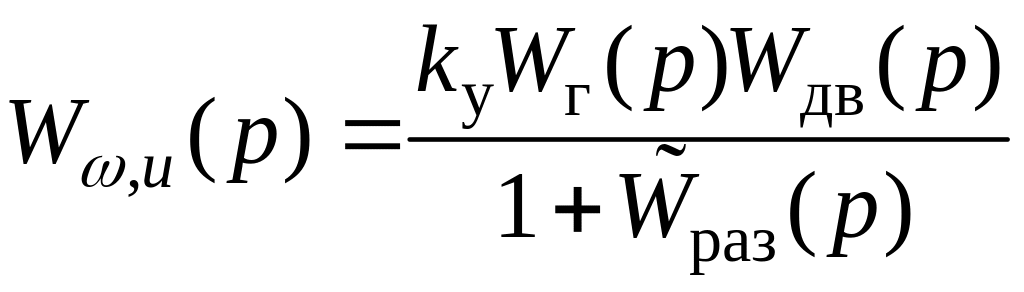Здесь в числителе указывается произведение передаточных функций кратчайшего пути от входа к выходу , в знаменателе выражение с передаточной функцией разомкнутой системы внутреннего контура .

Тогда передаточная функция определяется по формуле

,

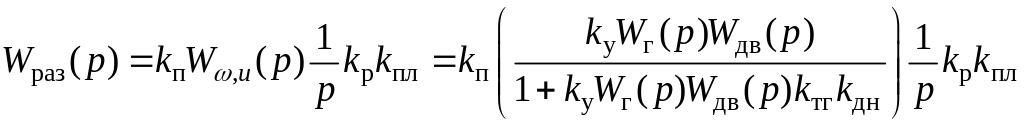а искомая передаточная функция имеет вид

б) Аналогично определяется передаточная функция . Сначала опре­деляется связь выхода со входом для внутреннего контура с помощью передаточной функции

,

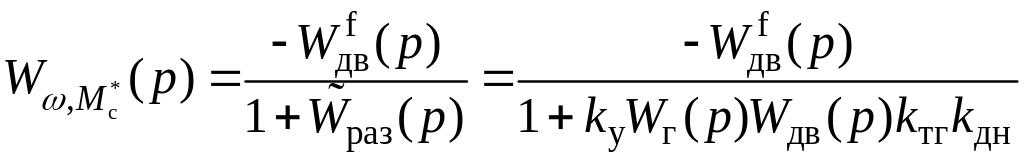где знак "–" соответствует знаку сигнала на устройстве сравнения. Затем при движе­нии по контуру от сигнала до сигнала окончательно находим вид передаточной функции