6. Расчет допусков на параметры четырехполюсника

Задание

Рассчитать допуски на входное и выходное сопротивление и коэффициент передачи четырехполюсника, содержащего четыре ветви (рис.1). Каждая ветвь содержит последовательно включенные резистор R, индуктивность L и конденсатор С. Две ветви, включенные параллельно, расположены в последовательной ветви, а две другие, тоже соединенные параллельно, включены к выходным клеммам четырехполюсника.

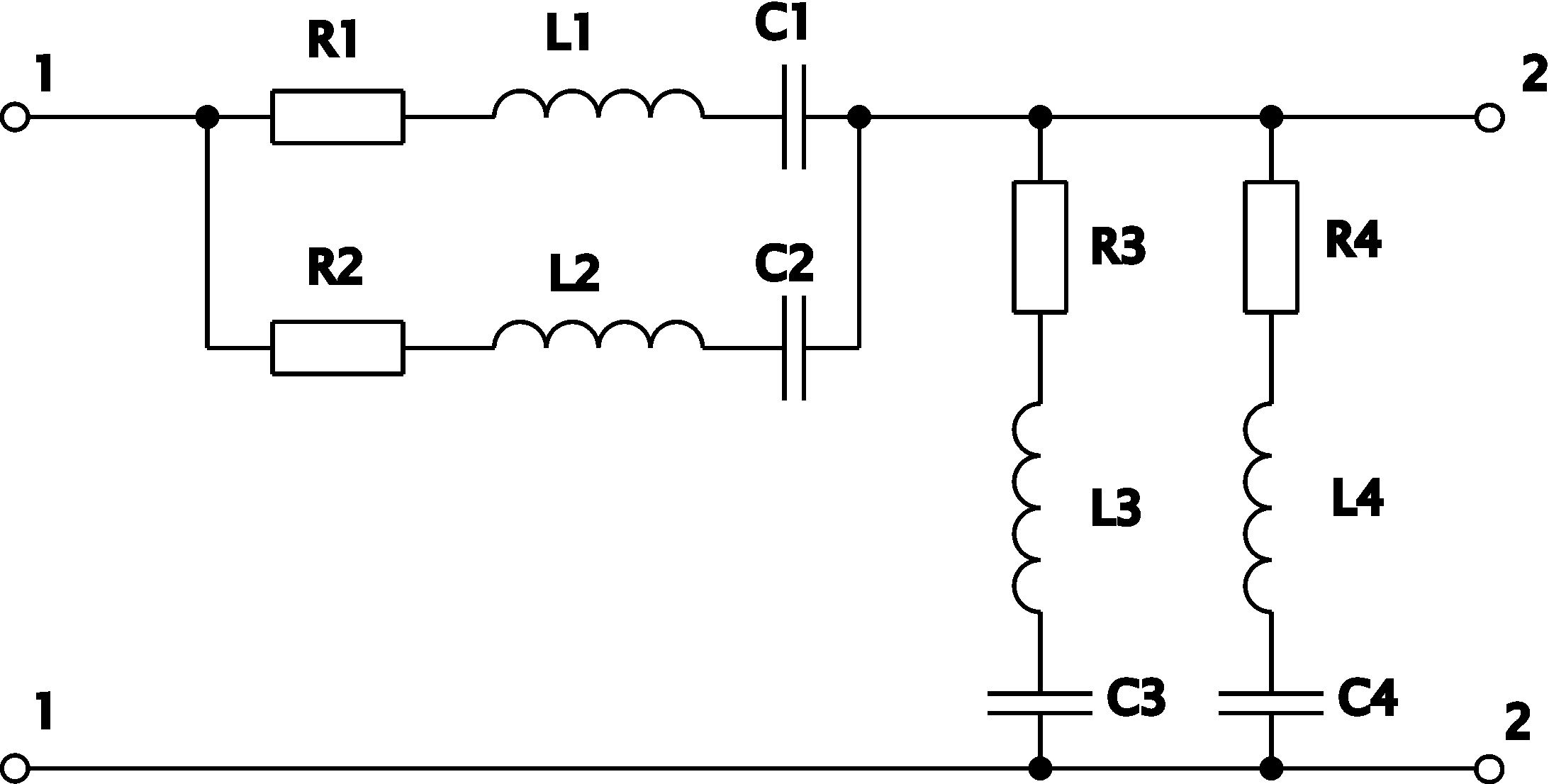
Рис. 1 Принципиальная схема электрического фильтра

Определить зависимость допусков от частоты и построить графики этих зависимостей. Величины индуктивности, сопротивления, емкости, частоты на которой производится расчет, а также погрешности изготовления элементов задаются преподавателем.

Задание

Произвести статическую обработку результатов измерений. Оценить стабильность технологического процесса, иcходя из того, что в течении рабочей смены было взято m выборок из N деталей каждая. Результаты контролируемого параметра деталей (не менее 50 значений) задаются преподавателем индивидуально каждому студенту.

Порядок вычислений:

1. Исключить из выборок ошибочные результаты, не характерные для данной совокупности.

2. Построить гистограммы и определить вид закона распределения.

3. Вычислить оценки математического ожидания и дисперсии контролируемого параметра.

4. Проверить гипотезы о равенстве дисперсий и математических ожиданий.

Расчеты работы проводятся на основании технического задания (Т3), в котором указывается [8,9]:

наименования расчетного задания;

характеристики и параметры ЭС;

условия эксплуатации.

6.1. Пример технического задания

Рассчитать допуски на входное и выходное сопротивления и коэффициент передачи четырехполюсника с заданными номиналами элементов, представленного на рисунке 2. Определить зависимости допусков от частоты, построить соответствующие графики.

Номиналы элементов четырехполюсника:

r₁ = 1 Ом; r₂ = 2 Ом; r₃ = 1 Ом; r₄ = 2 Ом;

L₁ = 400 мкГн; L₂ = 500 мкГн; L₃ = 600 мкГн; L₄ = 400 мкГн;

С₁ = 1200 пФ; С₂ = 1000 пФ; С₃ = 1000 пФ; С₄ = 1200 пФ.

Погрешности параметров элементов:

δr = ± 3 %; δL = + 3 %; δC= ± 3 %.

6.2. Определение параметров четырехполюсника

Для удобства определения параметров четырехполюсника определим комплексное сопротивление каждой ветви в общем виде:

(6.1)

где I – номер ветви; R_i L_i, C_i – параметры элементов, относящихся к i-ой ветви.

Определим общий вид параметров четырехполюсника в режиме холостого хода:

1) входное сопротивление:

, (6.2)

2) выходное сопротивление:

, (6.3)

3) коэффициент передачи:

. (6.4)

6.3. Расчет допусков на входное и выходное сопротивление и коэффициент передачи четырехполюсника

Т.к. требуется определить функциональную зависимость допусков от частоты, то воспользуемся расчетно-аналитическим методом оценки точности.

Пусть известна функциональная связь между каким-либо параметром устройства Y и параметрами q_i(i = 1,2...n) входящих в это устройство элементов. В самом общем виде она может быть записана:

. (6.5)

Очевидно, что всякие отклонения q приведут к отклонению Y. Чтобы установить между ними аналитическую связь в явном виде, воспользуемся правилами дифференциального исчисления. При этом будем предполагать, что величины q_i взаимонезависимы. Тогда полный дифференциал dY от (6) запишется:

(6.6)

Переходя от дифференциалов к конечным приращениям, т.е. полагая, что dq_i≈Δq_i, из (6.6) получим выражение абсолютной погрешности устройства ΔY в следующем виде:

(6.7)

Разделив (7) на (5), получим относительную погрешность устройства ΔY/Y в виде функции относительных погрешностей Δq_i/q_i, входящих в устройство элементов:

(6.8)

где Аi - весовые коэффициенты, характеризующие меру влияния (вклад) составляющих погрешностей Δq_i/q_i на выходную погрешность устройства δY=ΔY/Y.

Допуски можно подсчитать, используя формулы (6.7), (6.8):

; (6.9)

; (6.10)

(6.11)

В формулах (6.9), (6.10), (6.11) используются частные производные и абсолютные погрешности ΔZ_i, которые вычисляются следующим образом:

где

Погрешность сопротивления ΔZ_i вычисляем из формулы (6.7):

. (6.12)

Тогда

(6.13)

После подстановки всех формул и преобразований получим:

; (6.14)

; (6.15)

(6.16)

Посмотрим, как будет выглядеть зависимости Z_i от частоты:

Z₁= 1+(4*10^-4*ω - 8,3*10⁸/ω)*j; Z₂= 2+(5*10^-4*ω - 1*10⁸/ω)*j;

Z₃= 1+(6*10^-4*ω - 1 *10⁸/ω)*j; Z₄= 2+(4*10^-4*ω - 8,3*10⁸/ω)*j.

Согласно формулам (6.1)-(6.16) проведем расчет параметров фильтра для частоты 1*10⁶ рад/с:

Z₁= 1+400*10⁶*10^-6j+1/(1200*10⁶*10^-12j) = 1 - 433,333j = 433,334*e^-j1,568, Ом;

Z₂= 2+500*10⁶*10^-6j+1/(1000*10⁶*10^-12j) = 2 - 500j=500,004*e^-j1,567, Ом;

Z₃= 1+600*10⁶*10^-6j+1/(1000*10⁶*10^-12j) = 1- 400j = 400,001*e^-j1,568, Ом;

Z₄= 2+400*10⁶*10^-6j+1/(1200*10⁶*10^-12j) = 2 - 433,333j = 433,338*e^-j1,566, Ом;

Z_BX = 1,449 - 440,143j = 440,145*e^-j1,568, Ом;

Z_BЫХ = 0,731-208j = 208,001*e^-j1,567, Ом;

K= 0,473 + l,052*10^-4j = 0,473*e^{j 2,226*10^-4};

δZ_BX =0,13; δZ_BЫХ = 0,136; δК=0,136-0,1З = 0,006.