1.1.6 Несобственные интегралы

При введении понятия определённого интеграла мы предполагали, что подынтегральная функция является ограниченной, а пределы интегрирования – конечными. Такой интеграл называется собственным (слово «собственный» обычно опускается). Если хотя бы одно из этих двух условий не выполнено, то интеграл называется несобственным.

Интегралы с бесконечными пределами интегрирования

Пусть функция f(x) непрерывна при < , т.е. при Тогда по определению полагают

Если этот предел существует, то говорят, что интеграл

сходится, а если предел не существует, то интеграл называют расходящимся.

Геометрически для неотрицательной при функции f(x) несобственный интеграл по аналогии с собственным интегралом представляет собой площадь фигуры, ограниченной сверху графиком функции y=f(x), слева отрезком прямой x=a и снизу осью Ox.

Рис.10.

Что значит вычислить несобственный интеграл? Вычислить несобственный интеграл – это значит найти ЧИСЛО или доказать, что оно расходится. Несобственные интегралы бывают двух видов: несобственный интеграл с бесконечным пределом (амии) интегрирования и несобственные интегралы от неограниченных функций. Несобственный интеграл существует только тогда, когда подынтегральная функция непрерывна на интервале .

Несобственный интеграл численно равен площади заштрихованной площади фигуры, при этом возможны два случая:

1)Если фигура бесконечна , то , тогда говорят, что несобственный интеграл расходится.

2)Если , то несобственный интеграл сходится.

Важно! Когда для решения предложен любой несобственный интеграл, то, вообще говоря, ни о какой площади речь не идет и чертеж строить не нужно. Главное найти ЧИСЛО или доказать, что несобственный интеграл расходится.

Примеры:

1. Исследовать на сходимость интегралы:

а) т.е. данный несобственный интеграл сходится.

б) т.е. данный интеграл расходится.

в) Установим, при каких значениях интеграл сходится.

Случай был рассмотрен в примере б). Если то

.

Значит, данный интеграл сходится при >1 и расходится при

Аналогично определяются следующие несобственные интегралы

Интегралы от неограниченных функций

Пусть функция f(x) непрерывна при <b. Пусть эта функция стремится к бесконечности, когда (т.е. на отрезке функция f(x) не ограничена). Положим

Если этот предел существует, то говорят, что интеграл

сходится, а если предел не существует, то интеграл называют расходящимся.

Подобным же образом равенство

даёт определение интеграла от функции f(x), стремящейся к бесконечности при

Наконец, если функция f(x) стремится к бесконечности при приближении аргумента к обоим концам промежутка , то полагают

a<c<b.

Если при этом сходятся оба интеграла в правой части последнего равенства, то сходится и интеграл слева.

2.

, т.е. расходится.

1.2. Приложения интегрального исчисления в нефтегазовом деле.

• Объем добычи добычи нефти, произведенной за время T.

Пусть функция y=f(t) описывает изменение в добычи нефти на некотором месторождении с течением времени t. Найдем объем добычи u, произведенной за промежуток времени [0,T].

Отметим, что если производительность не изменяется с течением времени (f(t) – постоянная функция), то объем добычи , произведенной за некоторый промежуток времени , задается формулой .

Построим интегральную сумму. Разобьем отрезок [0,T] на промежутки времени точками: . Для величины объема добытой нефти , произведенной за промежуток времени , имеем:

, где

.

Тогда .

Перейдя к пределу при , найдем объем добытой нефти

.

По определению определенного интеграла

,

таким образом

.

Итак, если f(t) – производительность труда в момент t, то есть объем добытой нефти за промежуток [0,T].

• Применение теоремы о среднем.

Пусть известна функция t=t(x), описывающая изменение затрат времени t на освоение нового месторождения, где x – порядковый номер скважин. Тогда среднее время, затраченное на освоение одной скважины в период освоения от скважин, вычисляется по теореме о среднем:

.

Что касается функции изменения затрат времени на освоение месторождения t=t(x), то часто она имеет вид

,

где – затраты времени на освоение первой скважины, - показатель процесса.

Пример 1. Найти объём добытой нефти за 4 года, одной скважины, если функция Кобба-Дугласа имеет вид .

Решение:

Используем метод интегрирования по частям. Пусть , . Тогда , .

Следовательно,

( ).

• Давление жидкости. Рассмотрим вычисление величины давления жидкости на вертикальную пластинку, погруженную в жидкость.

Предположим, что ABCD (рис.10)представляет часть вертикальной пластинки, погруженной в жидкость, например часть вертикальной пластинки резервуара, наполненного жидкостью. Требуется вычислить величину давления на эту площадку. Расположим оси оси координат, как показано на рисунке, где ось OY выбрана совпадающей с уровнем жидкости. Разделим отрезок AB на n небольших интегралов и построим n прямоугольников, как это сделано на рисунке 10.

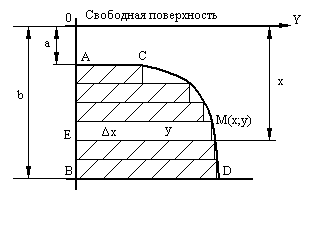
Рис.10.

Площадь одного прямоугольника (например, прямоугольника EM) равна . Если этот прямоугольник был расположен в горизонтальной плоскости на глубине x, считая от уровня жидкости в сосуде, то величина давления жидкости на прямоугольник была бы равна (величина давления жидкости на горизонтальную площадку равна весу столба жидкости, имеющего эту площадку своим основанием и высотой – расстояние площадки от свободной жидкости), где -вес единицы объема жидкости. Так как давление жидкости во все стороны одинаково, то отсюда следует, что есть элемент величины давления на пластинку. Следовательно, величина давления P на всю пластинку ABCD будет равна

(1).

Для фактического вычисления в данной формуле следует выразить y как функцию x из уравнения кривой CD, ограничивающей пластинку.

Вес кубического метра нефти будем считать равным 76 кг (= ).

Пример 2.Резервуар для нефти имеет форму лежащего цилиндра диаметром 6м, наполовину заполненную нефтью. Найти величину давления нефти на вертикальную заслонку, закрывающую резервуар.

Решение.

Уравнение окружности есть

,

следовательно, ,далее, =97 пределы интегрирования суть a=0, и b=3.

Подставляя эти значения в формулу (1), получим величину давления на вертикальную часть заслонки, расположенную вправо от оси OX (рис.1.12.1.),

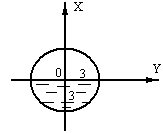
Рис.1.2.1.

.

Следовательно, величина давления на всю заслонку

.

• Работа. Если величина силы, действующей по направлению движения, постоянна, то под работой, произведенной силой, подразумевают произведение силы на путь , пройденной материальной точкой, где обозначает конечную, а точку движения. Если сила переменная, то работа может быть определена только с помощью предельного перехода. Мы разбиваем весь отрезок пути от до на n частей и предполагаем, что в каждом частичном небольшом интервале сила имеет постоянное значение, например то значение f(s), какое она принимает в некоторой произвольно взятой точке s этого интервала. Тогда произведение дает нам элементарную работу, а полная работа W, произведенная силой, выразится так:

.

Если направление действующей силы совпадает с направлением движения, то произведенная работа положительна, в противоположном случае работа отрицательна.

Пример 3. Резервуар для нефти имеет форму цилиндра (рис.1.2.2.)наполнен нефтью. Если высота h, а радиус основания r, то сколько времени потребуется чтобы что бы он опорожнился, если произойдет пробоина в основании с площадью a?

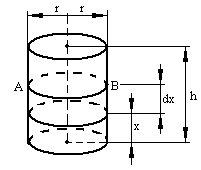
Рис.1.2.2.

Решение. Известно, что если пренебречь всеми осложняющими явление сопротивлениями, то скорость истечения через отверстие равна скорости, приобретаемое телом, свободно падающим с высоты, равной глубине нефти в сосуде. Следовательно, обозначая эту глубину буквой x, имеем:

Пусть в элемент времени dt вытекает объем dQ нефти, а соответствующее понижение поверхности назовем dx. В единицу времени вытекает из отверстия объем жидкости , измеряемый прямым цилиндром, площадь основания которого есть a , а высота v (= ).Следовательно, в течение времени dt вытекает

(а)

Но объем жидкости, вытекающий за время dt, можно рассматривать как объем цилиндра AB у которого площадь основания равна S,а высота равна dx, отсюда

(в)

Приравнивая (a) и (b) и решая относительно dt, имеем: , откуда

.