Глава 7. Задачи и упражнения
7.1. Повторение материала из курса
«ДИСКРЕТНАЯ МАТЕМАТИКА»
Совершенной
конъюнктивной нормальной формой
(СКНФ) логической функции
называют представление её в виде
конъюнкции макстермов, построенных из
аргументов рассматриваемой функции:
.
Совершенной
дизъюнктивной нормальной формой
(СДНФ)
логической функции
называют представление её в виде
дизъюнкции минтермов, построенных из
аргументов
:
.
Пример. Привести заданную логическую функцию к форме СДНФ с использованием обоих известных способов:
x |
y |
z |
|
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
Пример. Привести заданную логическую функцию к форме СКНФ с использованием обоих известных способов:
x |
y |
z |
|
|
|
f( x, y, z) |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
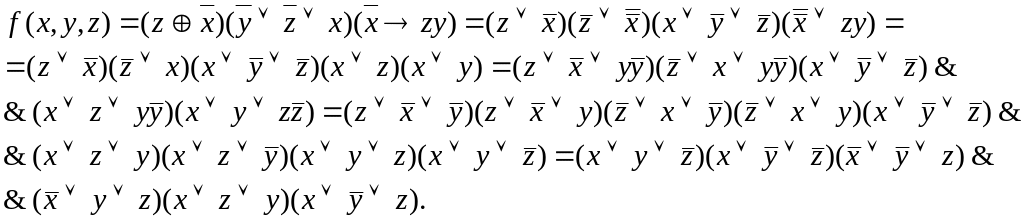
1. Построить таблицы истинности для заданной логической функции:
а)
;
б)
;
в)
;
г)
.
2. Привести заданную логическую функцию к форме СДНФ, используя табличный способ и способ эквивалентных преобразований:
а)
;
б)
;
в)
;
г)
.
3. Привести заданную логическую функцию к форме СКНФ, используя табличный способ и способ эквивалентных преобразований:
а)
;
б)
;
в)
;
г)
.