Завдання № 20 Рухи простору. Перетворення подібності

1. Знайти рівняння прямої , яка симетрична прямій 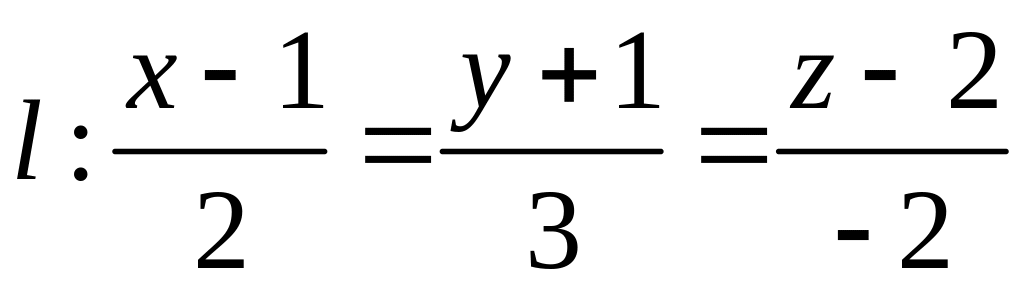відносно площини

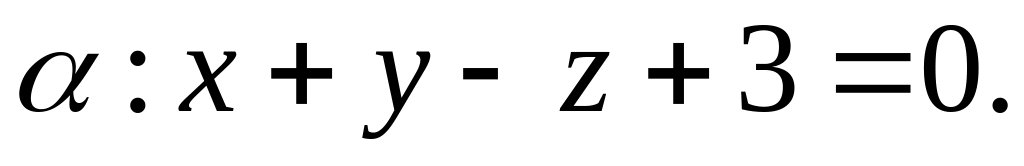
2. Дано точки . Відомо, що є образом точки при гомотетії з коефіцієнтом . Знайти центр гомотетії.

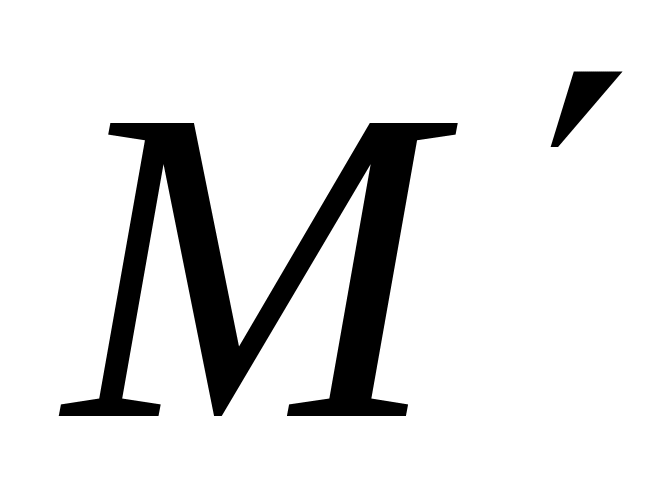3. Знайти координати точки , яку одержано з точки 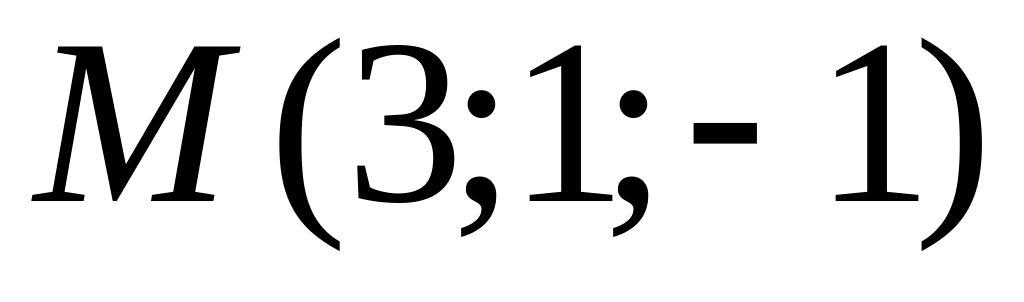при повороті на кут відносно прямої .

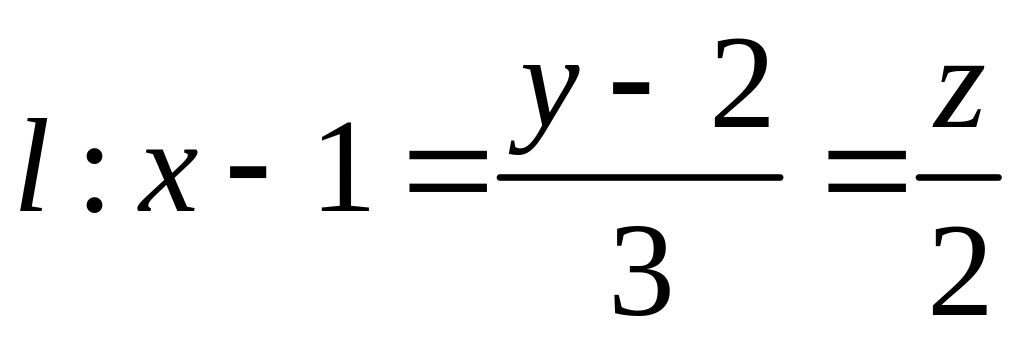4. Знайти рівняння прямої , яка симетрична прямій відносно точки

5. Перетворення подібності є композицією гомотетії з центром 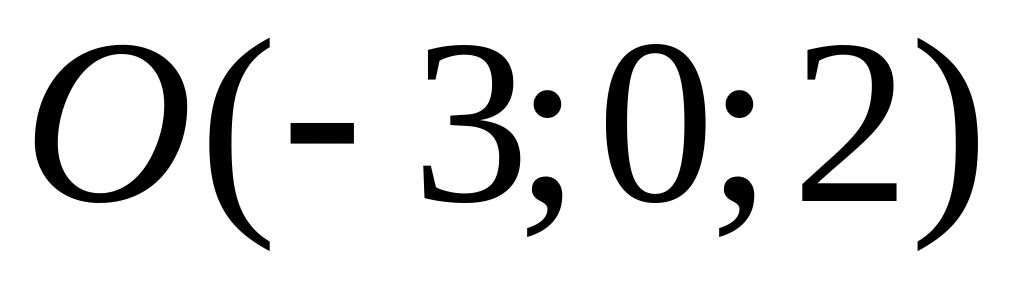і коефіцієнтом 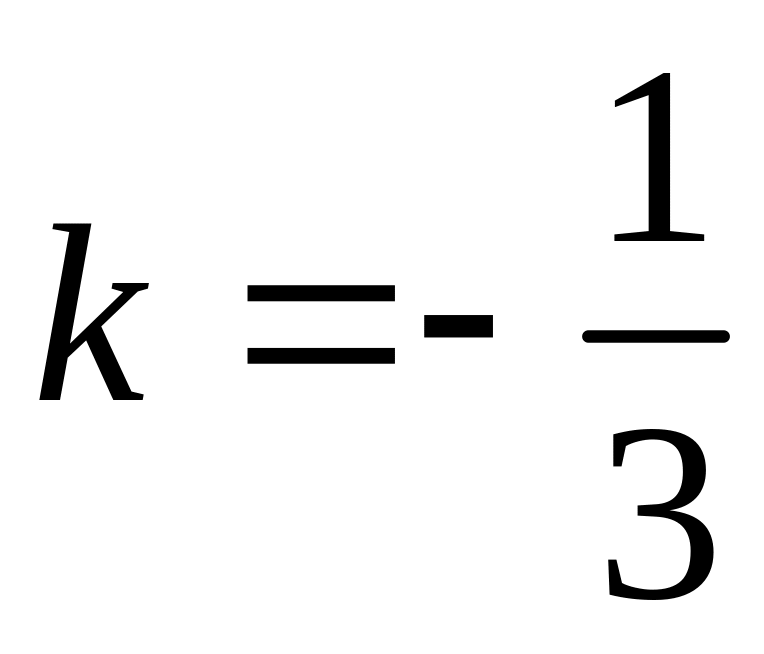та паралельного перенесення на вектор . Знайти координати точки , яка є образом точки .

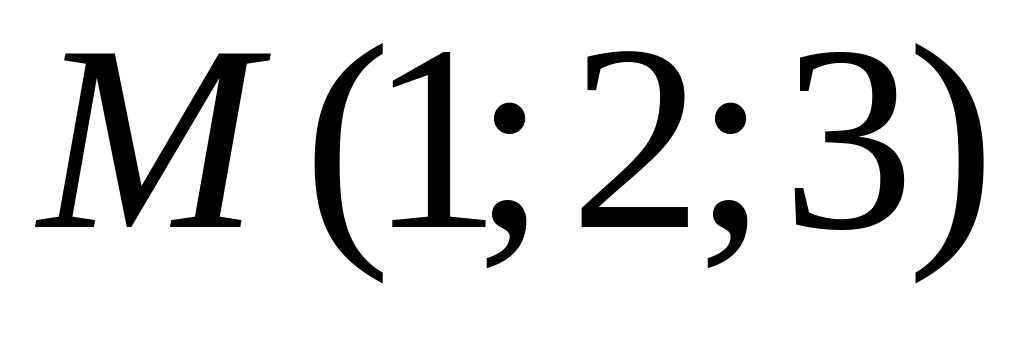6. Дано точки 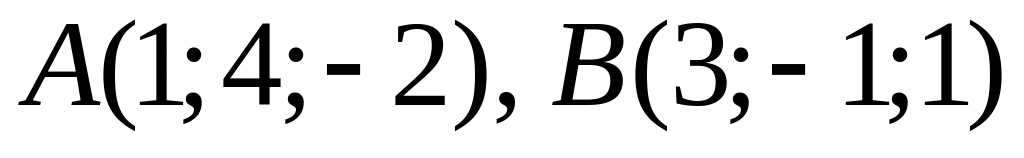та 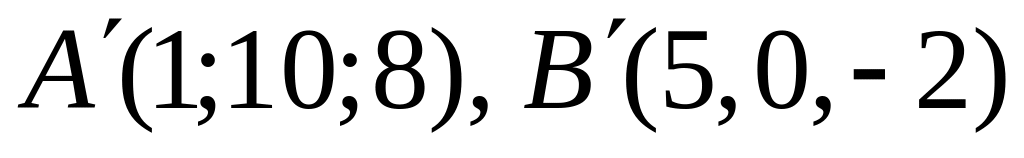, які є їхніми образами при гомотетії з коефіцієнтом 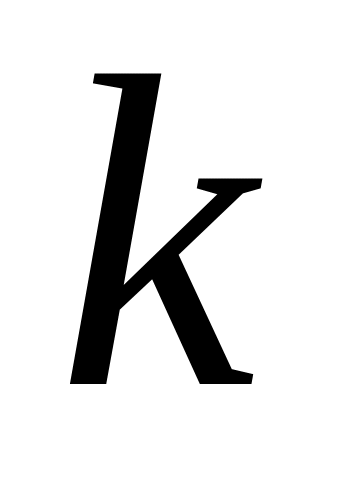і центром . Знайти та .

7. Дано площину і вектор , який паралельний до площини. Знайти координати точки , яку одержано з точки при сковзній симетрії, яка задана площиною і вектором .

8. Дано точки 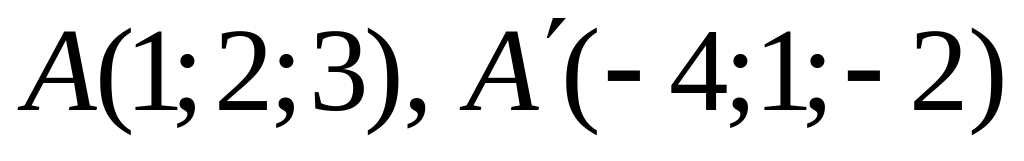. Відомо, що є образом точки при гомотетії з коефіцієнтом . Знайти центр гомотетії.

9. Знайти рівняння прямої , яка симетрична прямій 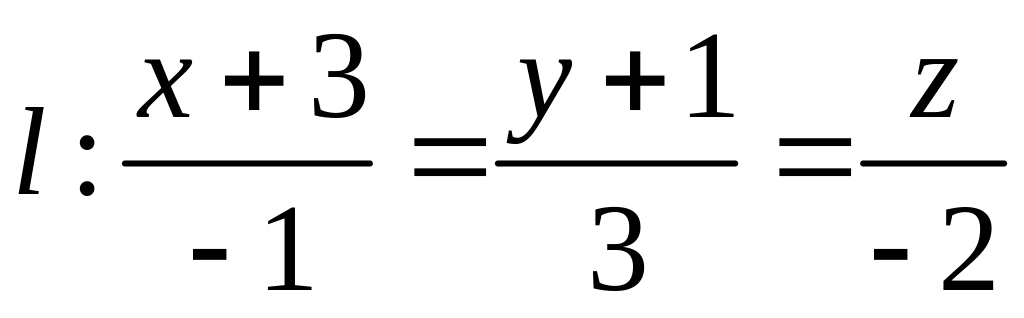відносно площини

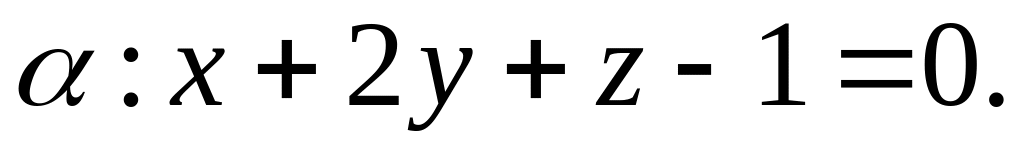
10. Перетворення подібності є композицією гомотетії з центром і коефіцієнтом 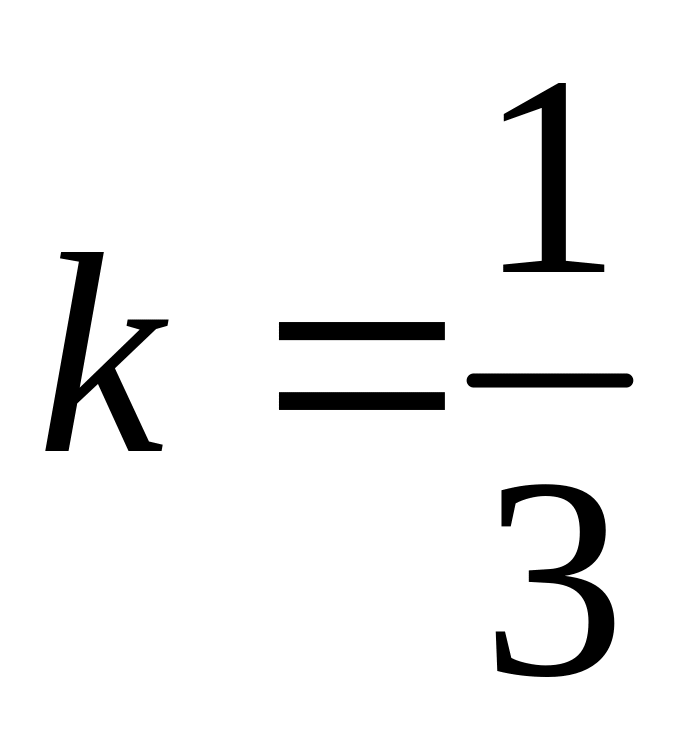та паралельного перенесення на вектор 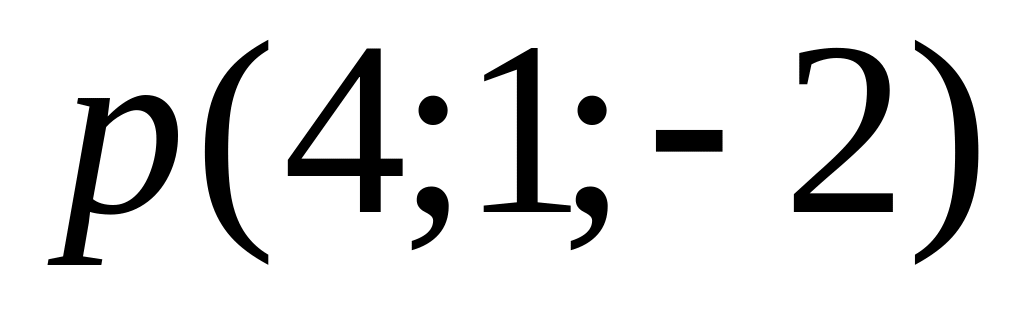. Знайти координати точки , яка є образом точки .

24