
- •Аналітична геометрія Індивідуальні завдання
- •Завдання для індивідуальної роботи модуль б (рік навчання 1, семестр 2)
- •Завдання № 1 Системи координат у просторі
- •Завдання № 2 Застосування методу координат до розв’язування задач елементарної геометрії
- •Завдання № 3 Рівняння площини
- •Завдання № 4 Взаємне розміщення площин
- •Завдання № 5 Метричні задачі з теорії площин
- •Завдання № 6 Канонічні рівняння прямої у просторі
- •Завдання № 10 Застосування теорії прямих і площин до розв’язування задач елементарної геометрії
- •Завдання № 11 Циліндричні поверхні
- •Завдання № 12 Конічні поверхні
- •Завдання № 13 Поверхні обертання
- •Завдання № 14 Еліпсоїд. Параболоїди. Гіперболоїди
- •Завдання № 20 Рухи простору. Перетворення подібності
Завдання № 3 Рівняння площини
Точка Р(2;-1;-1) є основою перпендикуляра, проведеного з початку координат на площину. Скласти рівняння цієї площини.
Скласти рівняння площини, яка проходить через початок координат паралельно площині
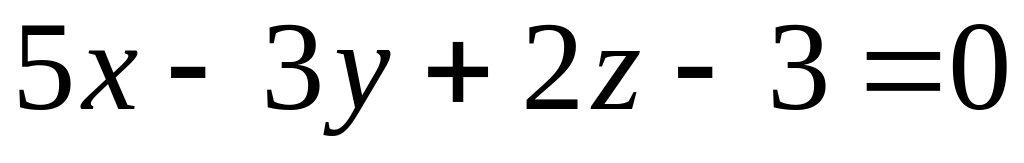 .
.
Скласти рівняння площини, яка проходить через точку М(3;-2;-7) паралельно площині
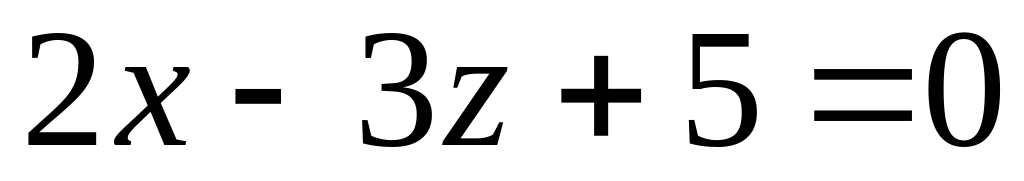 .
.
Скласти рівняння площини, яка проходить через початок координат перпендикулярно до двох площин
 і
і
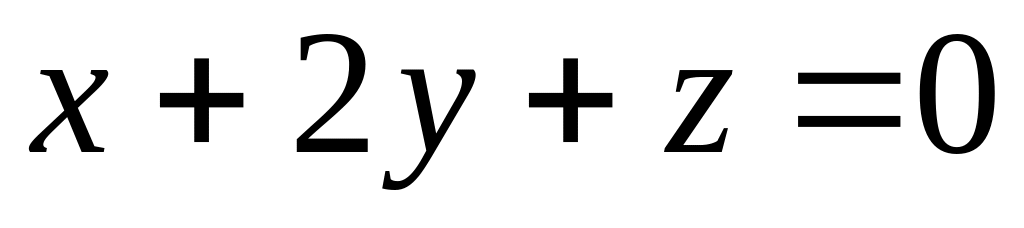 .
.
Скласти рівняння площини, яка проходить через дві точки М1(1;-1;-2), M2(3;1;1) перпендикулярно до площини
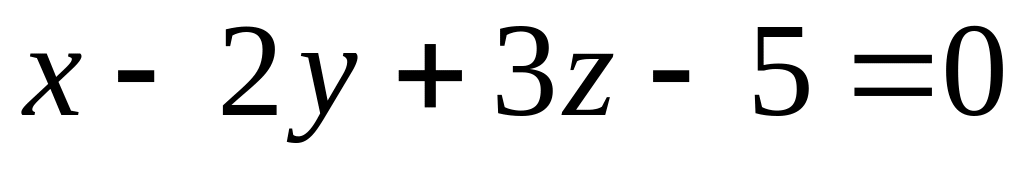 .
.
Скласти рівняння площин, які проходять через точку М1(2;-3;3) паралельно до відповідних координатних площин.
Скласти рівняння площини, що проходить через точки М1(7;2;-3) і М2(5;6;-4) паралельно до вісі Ох.
Площина проходить через точку М1(6;-10;1) і відтинає на вісі абсцис відрізок
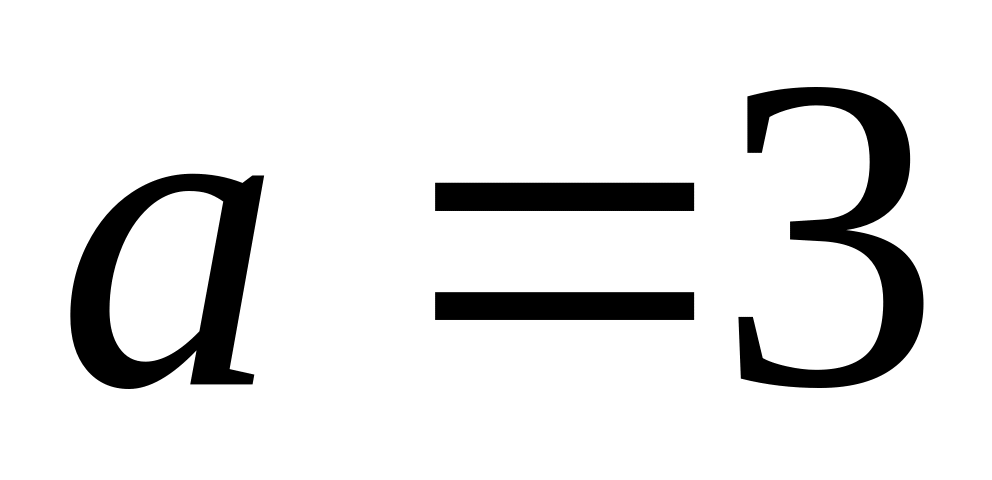 ,
а від осі аплікат відрізок
,
а від осі аплікат відрізок
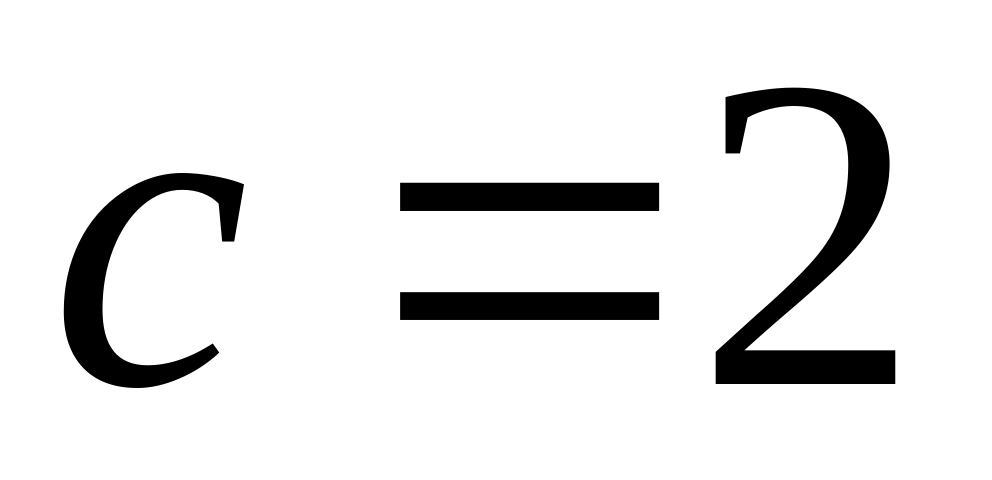 .
Скласти рівняння цієї площини у
відрізках.
.
Скласти рівняння цієї площини у
відрізках.
Скласти рівняння площини, яка відтинає на вісі Oz відрізок
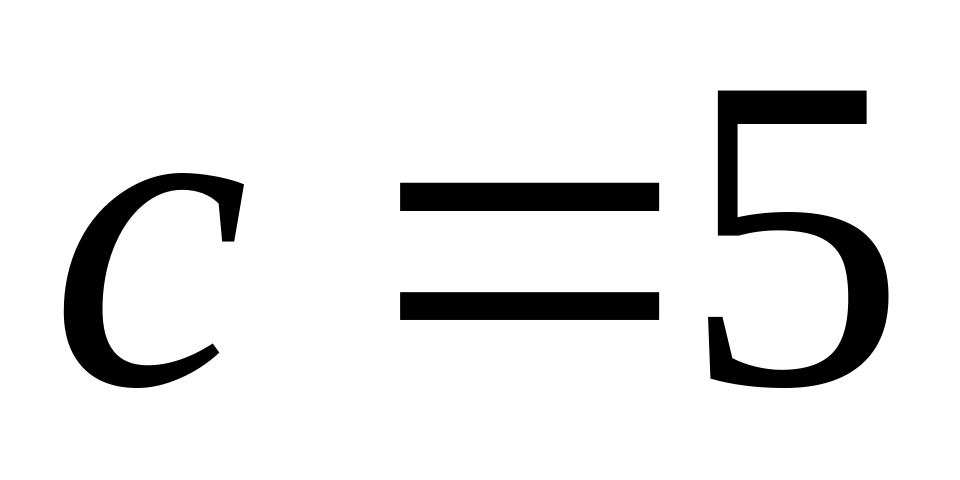 і перпендикулярна до вектора
і перпендикулярна до вектора
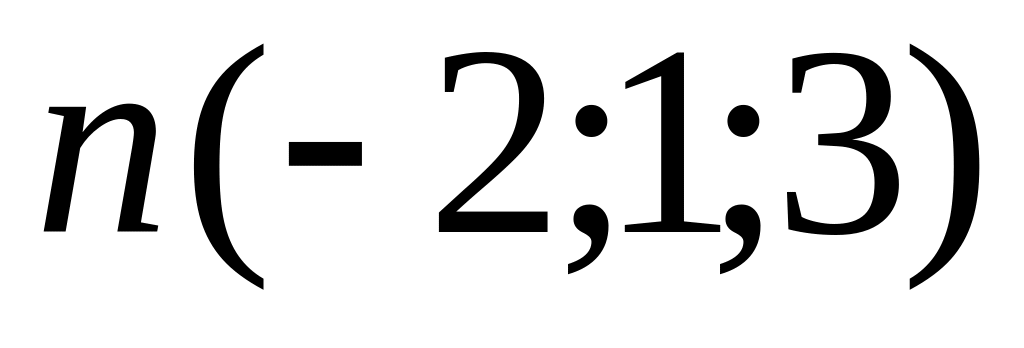 .
.
Скласти рівняння площини, яка паралельна вектору
 і відтинає на координатних осях Ох
і Оу
відрізки
і відтинає на координатних осях Ох
і Оу
відрізки
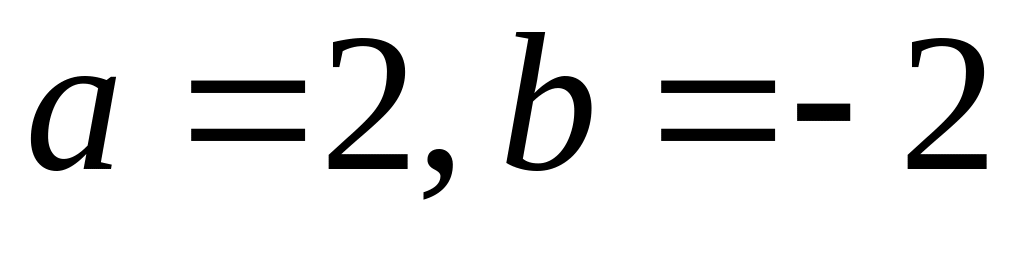 відповідно.
відповідно.
Завдання № 4 Взаємне розміщення площин
Визначити, які з наступних пар рівнянь задають паралельні площини (пояснити чому):
1)
![]() і
і
![]() ;
;
2)
![]() і
і
![]() ;
;
3)
![]() і
і
![]() .
.
Визначити, які з наступних пар рівнянь задають перпендикулярні площини (пояснити чому):
1)
![]() і
і
![]() ;
;
2)
![]() і
і
![]() ;
;
3)
![]() і
і
![]() .
.
Визначити, при яких значеннях l і m наступні пари рівнянь будуть задавати паралельні площини:
1)
![]() і
і
![]() ;
;
2)
![]() і
і
![]() ;
;
3)
![]() і
і
![]() .
.
Визначити, при яких значеннях l наступні пари рівнянь будуть задавати перпендикулярні площини:
1)
![]() і
і
![]() ;
;
2)
![]() і
і
![]() ;
;
3)
![]() і
.
і
.
Встановити взаємне розміщення трьох площин
 ,
,
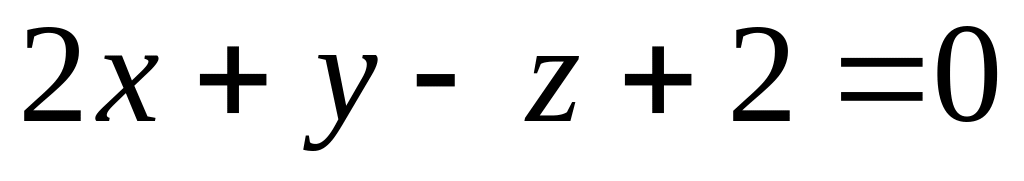 і
і
 .
.Встановити взаємне розміщення трьох площин
 ,
,
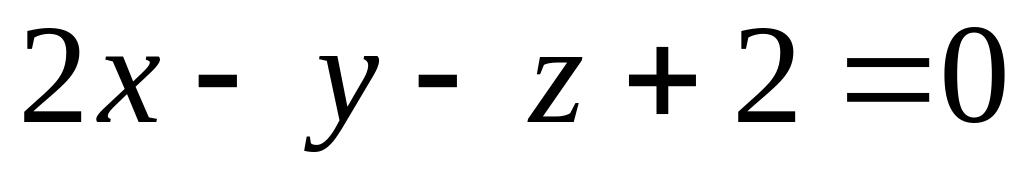 і
і
 .
.Встановити взаємне розміщення трьох площин
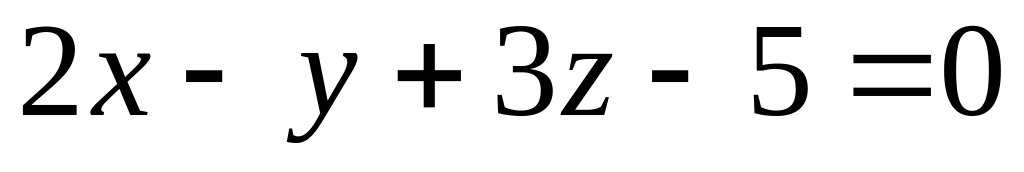 ,
,
 і
і
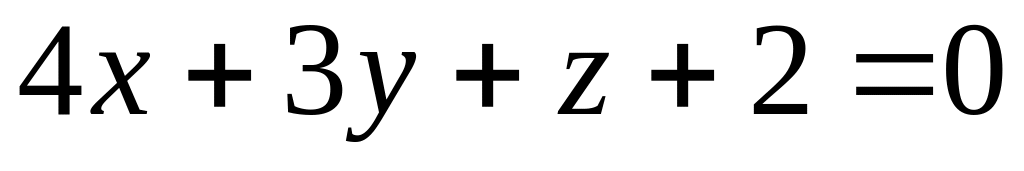 .
.Встановити взаємне розміщення трьох площин , і .
Визначити, при яких значеннях a і b площини
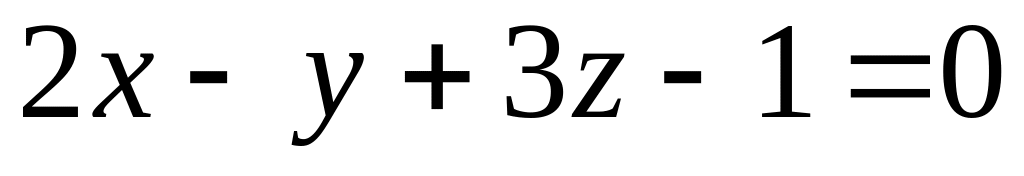 ,
,
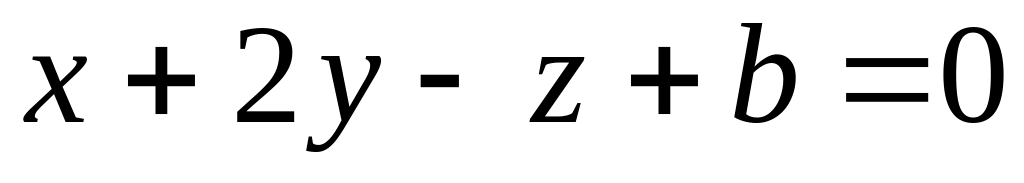 і
і
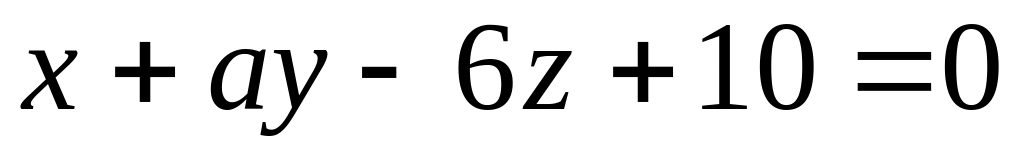 мають одну спільну точку.
мають одну спільну точку.Визначити, при яких значеннях a і b площини , і проходять через одну пряму.
Завдання № 5 Метричні задачі з теорії площин
Через вісь Оz провести площину, що утворює з площиною
 кут
кут
 .
.
Через точку А(1;2;3) провести площину, що перпендикулярна до площини
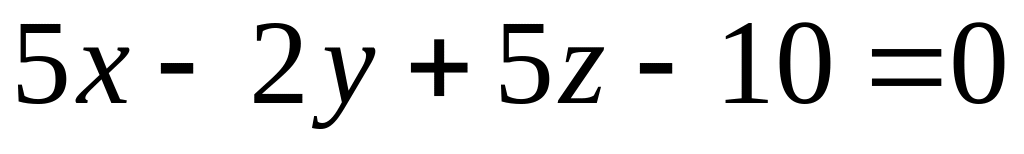 і утворює з площиною
і утворює з площиною
 кут
кут
 .
.
Вершини тетраедра знаходяться в точках А(0;0;2), В(3;0;5), С(1;1;0) і D(4;1;2). Обчислити довжину висоти, проведеної з вершини D на грань АВС.
Скласти рівняння бісекторних площин двогранних кутів між двома площинами
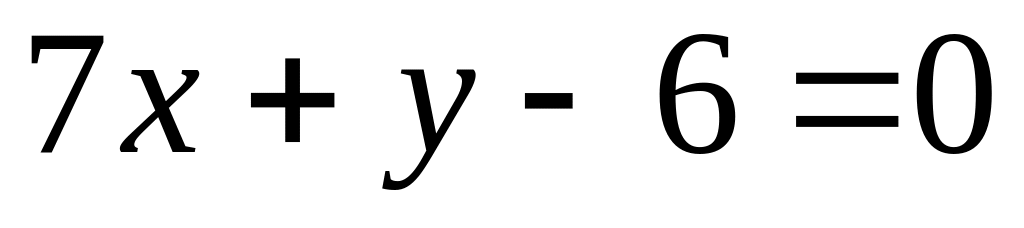 і
і
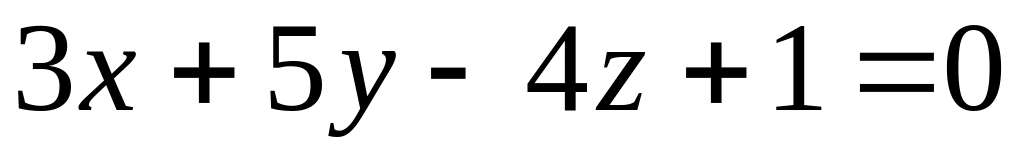 .
.
На вісі Оz знайти точку рівновіддалену від точки М(2;3;4) і площини
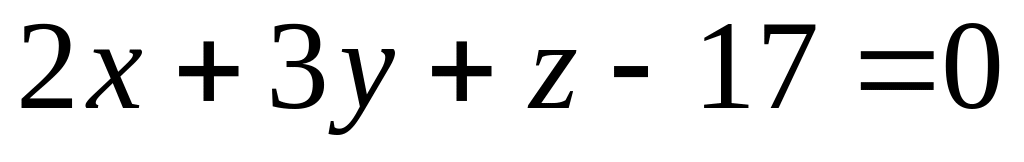 .
.
Скласти рівняння площини, яка знаходиться на відстані
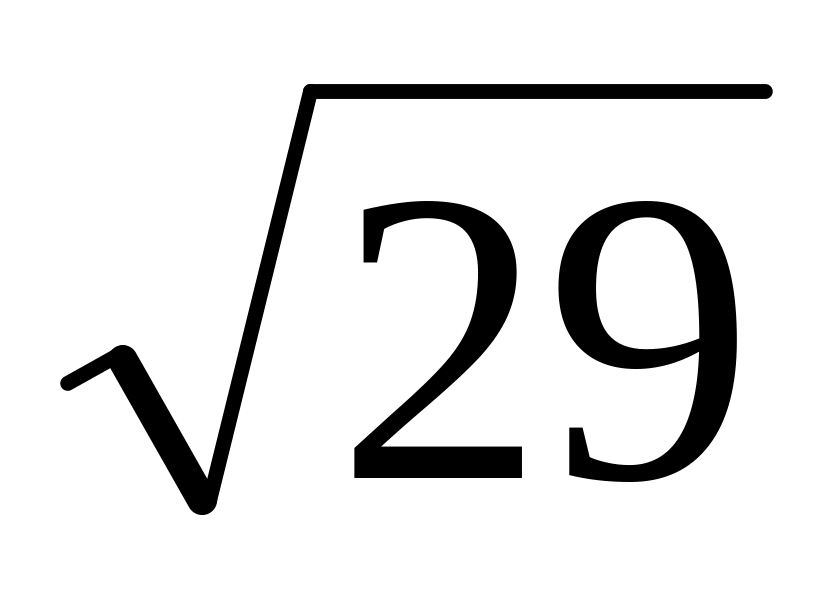 від початку координат і перпендикулярна
до прямої перетину площин
від початку координат і перпендикулярна
до прямої перетину площин
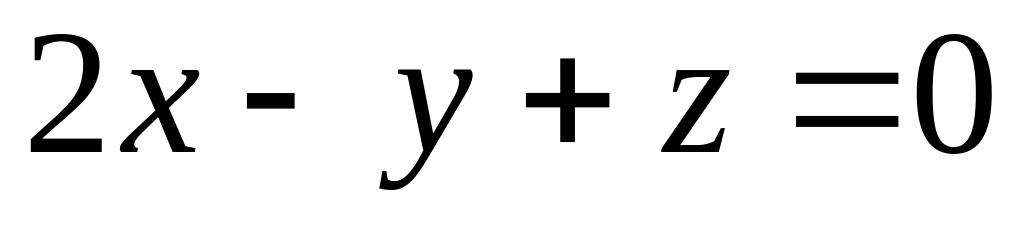 і
і
 .
.
Написати рівняння площини, що відтинає на осях координат відрізки, пропорційні числам 1, 2, 3 і знаходиться від точки М(3;5;7) на відстані 4.
Знайти відстань між площинами
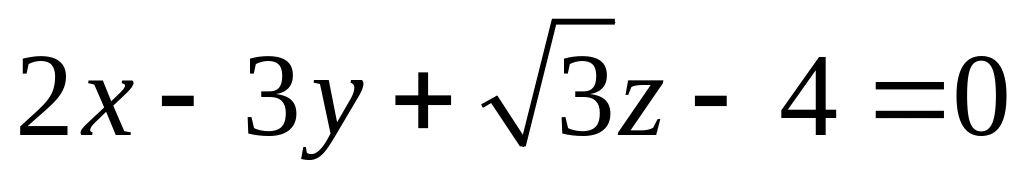 і
і
 .
.
Скласти рівняння площин, які паралельні площині
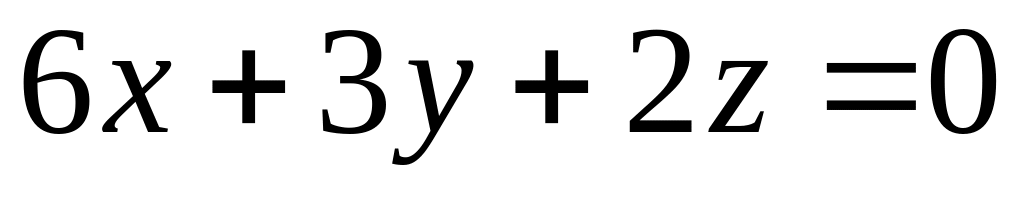 і знаходиться від точки
і знаходиться від точки
 на відстані 3.
на відстані 3.
Скласти рівняння бісекторних площин двогранних кутів між двома площинами
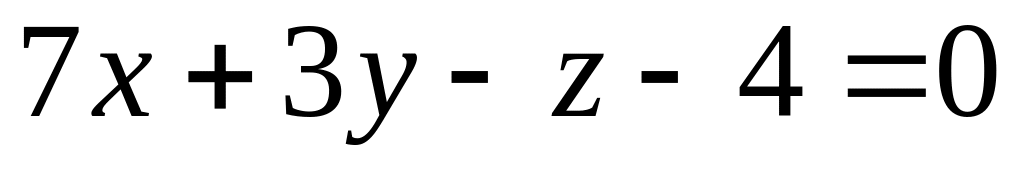 і
і
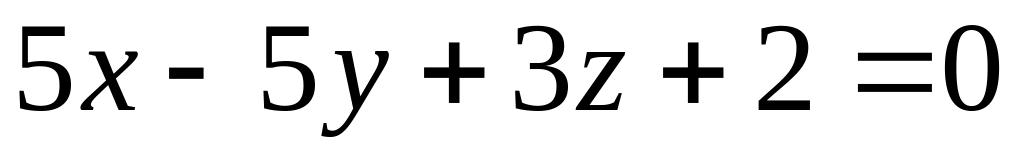 .
.
