1. Перша нормальна форма

Для першої нормальної форми потрібно, щоб таблиця була двовимірною і не містила груп, що повторюються. У таких таблиць є тільки дві характеристики – довжина (кількість записів або рядків) та ширина (кількість полів або стовпців). Вона не повинна містити комірок, що включають кілька значень. Для того, щоб в одній комірці містилося кілька величин, необхідно ввести третій вимір – глибину, за допомогою якої можна зберігати в одній комірці одразу декілька значень.

2. Друга нормальна форма

Для другої нормальної форми потрібно, щоб дані у всіх не ключових стовпцях повністю залежали від первинного ключа і кожного елемента (стовпця) первинного ключа, якщо ключ є складеним. Під повною залежністю розуміються те, що значення в кожному не ключовому стовпці однозначно визначається значенням первинного ключа. Якщо одне з полів не залежить від величини первинного ключа, то необхідно включити в ключ доповнювальні таблиці. Перед перевіркою на відповідність другій нормальній формі таблиця повинна бути приведена до першої нормальної форми. Друга нормальна форма дозволяє видалити більшу частину даних, що повторюються, які часто залишаються після першого етапу нормалізації.

3. Третя нормальна форма

Для третьої нормальної форми потрібно, щоб всі неключові стовпці таблиці не тільки залежали від первинного ключа таблиці, але були незалежними один від одного, тобто, щоб були відсутні транзитивні функціональні залежності між стовпцями таблиці. Для цього потрібно, щоб таблиці були попередньо приведені до першої та другої нормальної форми.

Реляційне відношення перебуває в тій чи іншій нормальній формі, якщо задані на ньому функціональні залежності задовольняють певні умови. Відношення, які не перебувають у відповідній нормальній формі, мають певні небажані властивості, або аномалії. Відтак виникає потреба в нормалізації, орієнтованій на те, щоб по­збавити реляційні відношення цих властивостей. Аномалії виникають унаслідок того, що реляційні відношення можуть містити надлишкові функціональні за­лежності, тобто кількість атрибутів відношення може бути завеликою, і тоді постає питання про коректність його схеми. Коректною вважається схема, що не містить небажаних функціональних залежностей. Виправлення некоректних схем здій­снюється за допомогою процедури декомпозиції (розкладання) реляційного від­ношення на множину інших відношень. Мета цієї процедури — побудова множи­ни таблиць без небажаних функціональних залежностей та аномалій. Це і є суттю процесу нормалізації. Іншими словами, нормалізація - це зворотний процес замі­ни даної схеми реляційних відношень іншою схемою, в якій відношення мають просту й коректну форму. Зворотність нормалізації означає, що після її здійснен­ня зберігається можливість повернення відношення до початкового стану.

Е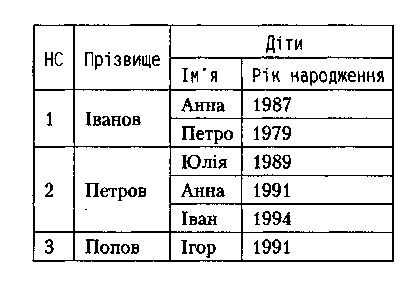 . Кодд спочатку визначив три рівні нормалізації, які він назвав першою, дру­гою і третьою нормальними формами (1НФ, 2НФ і ЗНФ). Згодом Р. Фейджин визначив четверту нормальну форму, в якій перебувають деякі відношення, що мають ЗНФ. Нарешті, була визначена ще одна форма, п'ята.

Складені домени і перша нормальна форма

Реляційна модель не допускає використання складених (неатомарних) доменів, тобто на перетині рядка і стовпця у таблиці має стояти атомарне значення, непо­дільне з точки зору всіх його можливих застосувань. Реляційне відношення пере­буває в першій нормальній формі (1НФ), якщо всі його атрибути мають атомарні (прості) домени, відтак значення елементів таблиці є простими. Реляційне відно­шення називається нормалізованим, якщо воно перебуває в 1НФ.

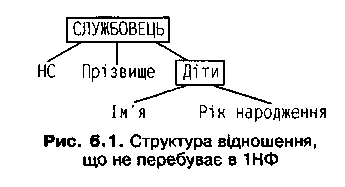
Н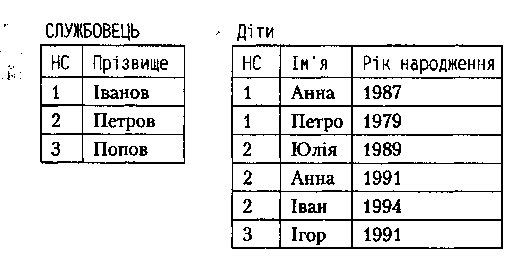 а рис. 6.1 зображено структуру відношення СЛУЖБОВЕЦЬ, побудованого на ато­марних доменах НС (номер службовця) і Прізвище та складеному домені Діти. Ця структура є деревоподібною і тому відношення не перебуває в 1НФ.

Розглянемо екземпляр відношення СЛУЖБОВЕЦЬ.

У 1НФ цей екземпляр відношення зображуватиметься у вигляді двох таблиць:

Р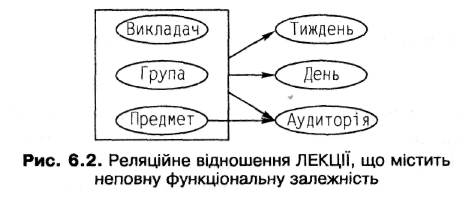 еляційна модель даних означена лише для тих відношень, що перебувають у першій нормальній формі.

Неповні функціональні залежності та друга нормальна форма

Нехай на реляційному відношенні R задано набори атрибутів Л і В. Функціональ­на залежність RA  R.B називається повною, якщо В не залежить функціонально від жодного піднабору що не містить В.

На рис. 6.2 атрибут Аудиторія неповно залежить від набору атрибутів Викладач, Група, Предмет, оскільки він залежить і від одного атрибуту Предмет, що входить до складу цього набору.

Реляційному відношенню ЛЕКЦІЇ властиві аномалії, що пов'язані з операціями маніпулювання даними. Пояснимо, чому ці аномалії виникають.

Якщо в предметній області є функціональна залежність Л -» В, це свідчить про наявність множини сутностей, складених з атрибутів (Л, В), причому група атри­бутів Л є унікальним ідентифікатором сутностей цієї множини (ключем), а В — їхньою властивістю. Оскільки атрибут Аудиторія функціонально залежить від ат­рибута Предмет, то в нашій предметній області на цій парі атрибутів визначена ок­рема множина сутностей. Проте ми не зможемо незалежно маніпулювати сутностями даної множини, оскільки це призведе до таких аномалій.

Аномалія додавання. Ми не зможемо відобразити той факт, що в конкретній аудиторії читаються лек­ції з конкретного предмета доти, доки не будуть визначені викладач і група.

Аномалія видалення. Видаляючи рядок з таблиці ЛЕКЦІЇ, ми можемо видалити унікальну (таку, якої більше ніде не міститься) інформацію про те, що певний предмет читається в пев­ній аудиторії.

Аномалія оновлення. Одне й те саме значення атрибута Аудиторі я для даного предмета повторюється багато разів. Тому, якщо предмет став читатися в іншій аудиторії, необхідно буде замінити номер аудиторії в усіх рядках таблиці ЛЕКЦІЇ.

З поняттям повної функціональної залежності пов'язане поняття другої нор­мальної форми.

Реляційне відношення перебуває в другій нормальній формі (2НФ), якщо воно перебуває в першій нормальній формі й усі його непервинні атрибути функціо­нально повно залежать від певного можливого ключа.

Друга нормальна форма нейтралізує аномалії, пов'язані з неповними функціо­нальними залежностями. Звести відношення до другої нормальної форми можна лише шляхом його поділу (декомпозиції) принаймні на два інших. Але цей поділ має відповідати таким умовам:

♦ відношення, які отримуємо в результаті, є проекціями початкового;

♦ початкове реляційне відношення можна відновити з кінцевих за допомогою операції природного з'єднання без втрат даних;

♦ під час декомпозиції не втрачаються функціональні залежності (тобто множини залежностей початкового й кінцевого відношень є еквівалентними). Шлях до вирішення цієї проблеми дає теорема, доведена І. Хітом.

Транзитивні залежності й третя нормальна форма

Поняття функціональної транзитивної залежності добре відоме в класичній тео­рії множин та теорії відношень. У реляційному підході використовується більш вузьке тлумачення цього терміна.

Набір атрибутів С транзитивно залежить від набору атрибутів А, якщо існує такий набір атрибутів В, що А -» В, В -> С і В - А. Останньою умовою реляційний варіант означення відрізняється від класичного.

Наявність у реляційному відношенні транзитивної залежності призводить до тих самих аномалій, що й наявність неповної функціональної залежності. Якщо в R (А, В, С) є функціональні залежності А -> В та В -> С, то таке відношення міс­тить інформацію про дві множини сутностей: (А, В) та (В, С), що призводить до аномалій додавання, видалення й оновлення.

З поняттям функціональної транзитивної залежності пов'язане поняття третьої нормальної форми.

Реляційне відношення перебуває в третій нормальній формі (ЗНФ), якщо во­но перебуває в другій нормальній формі й не містить транзитивних функціональ­них залежностей непервинних атрибутів від можливих ключів.

Третя нормальна форма вимагає відсутності транзитивної залежності саме не­первинних, а не всіх атрибутів відношення. Тому відношення НАВЧАННЯ, функціо­нальні залежності якого зображені на рис. 6.3, перебуває в ЗНФ.

В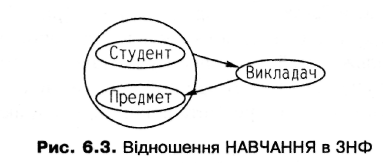 ідношенню в ЗНФ також властиві аномалії додавання, видалення й оновлен­ня. У зв'язку з цим вводиться поняття посиленої ЗНФ і нормальної форми Бойса-Кодда.

Якщо відношення перебуває в третій нормальній формі та не містить непов­них і транзитивних залежностей будь-яких атрибутів від можливих ключів, то во­но перебуває в посиленій ЗНФ.

Реляційне відношення перебуває в нормальній формі Бойса-Кодда (НФБК), коли воно має таку властивість: якщо довільний атрибут відношення, що не нале­жить набору атрибутів А, залежить функціонально від А, то й усі атрибути відно­шення функціонально залежать від А.

Поняття посиленої ЗНФ і НФБК еквівалентні, й тому їх часто вживають як синоніми.

Алгоритм зведення до посиленої третьої нормальної форми такий самий, як і до ЗНФ. Наприклад, у результаті нормалізації зображеного на рис. 6.3 відно­шення (воно не перебуває у посиленій ЗНФ) буде отримано два такі відношення:

ВИКЛАДАННЯ(Студент, Викладач) і ДИСЦИПЛІНА(Викладач, Предмет).

Нефункціональні залежності

Найбільш сильним критерієм якості схеми реляційної бази даних, який можна сформулювати виходячи з поняття функціональної залежності, є нормальна фор­ма Бойса-Кодда. Проте між атрибутами відношення можуть існувати не лише функціональні залежності. Узагальненням цього поняття є багатозначна залеж­ність, через яку означується четверта нормальна форма. Так само, узагальненням поняття багатозначної залежності є залежність за з'єднанням — це поняття засто­совується в означенні п'ятої нормальної форми. 5НФ є остаточною щодо операції проекції, тобто якщо відношення перебуває у 5НФ, воно не містить аномалій, які можуть бути усунені шляхом його поділу на проекції. Це не означає, що відно­шення у 5НФ зовсім не містить аномалій. Тому існують й інші нормальні форми, які використовуються рідше і розгляд яких виходить за межі завдань, що розгля­даються в даному посібнику.