3. Другий закон термодинаміки
4.1 Рівняння те термодинамічні залежності
Перший закон термодинаміки установлює еквівалентність тепла в роботу або роботи в тепло.
Другий закон термодинаміки показує напрямок процесів переходу тепла від одного тіла до другого. За допомогою другого закону термодинаміки можливо визначити степінь удосконалення процесу переходу тепла в роботу в теплових двигунах. Перехід тепла в роботу в них виникає за рахунок кругових процесів чи циклів. Для уцінення степені удосконалення любого цикл}' вводять термічний коефіцієнт корисної дії St, який визначають як відношення корисно витраченого тепла Q2 до всього підведеного тепла Q1, тобто:
St =
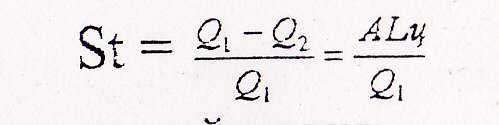
а для циклу Карно це рівняння приймає вид:
St =
Математичне вираження другого закону:
S - ентропія системи;
Q - теплота, що передається системі;
А - робота системи;
Заміна вільної енергії при V = const дорівнює:
( F)·ν = U - Т· S при V = соnst
( F)·ν = Y - Т· S
де U – зміна внутрішньої енергії;
Y – ентальпія;
Розрахуємо енергію Гіббса:
ΔG
Т2
– ΔG
Т1
= - Δа·Т2LnТ1
+ Δа·Т2
- Δа·Т1
-
+
-
-
-(ΔSТ1
+ ΔаLnТ1
– ΔbТ1
-
)·(Т
– Т1);
ΔG Т2 – ΔG Т1 = 25,05·400·2,3 Lg - 25,05·300·2,3 Lg 300 - 25,05·400 + 25,05·300 -
-
-
-
- (99,15
– 25,05·2,3 Lg 300 + 18,46·10-3·300
+
)·
·х (400 - 300) = 10315 Дж/моль
=
+ 10315 = - 16635 + 10315 = - 6320 Дж/моль.
4. Максимально-корисна робота
4.1 Основні залежності та розрахункові формули
Максимальна робота відповідно до другого Закону термодинаміки дорівнює:
АМ ≤ (U - TS) (4.1)
Функція (U- TS) - це енергія Гельмгольца (ізохорно-ізотермічний потенціал) і визначається F, тоді:
F = U-TS (4.2)
Для любого ізотермічного процесу ізохорно-ізотермічний потенціал визначається по рівнянням:
dF = Du – T·dS
F = U – T· S
Максимальна робота в ізотермічному процесі
АМ = - Г
Для систем, що знаходяться при постійному тиску і температурі, розраховується енергія Гіббса, яка
G = H-TS (4.3)
Для любого процесу:
G = F + P· V
Максимально-корисною роботою ізотермічного процесу називають величину
A
= -
G
A = АМ - P· V
Максимально-корисна робота при заданих температурі і тиску дорівнює зміні ізобарно-ізотермічного потенціала системи (або зміні вільної ентальпії, енергії Гіббса)
G
=
H
+ T·
S
=
H
- T
vh - зміна ентальпії в ході процесу
Т - температура
VS - зміна ентропії
3Q - безкінцево мала зміна кількості тепла
Коли об’єм в ході реакції не змінюється, а тепло реакції витрачається на
нагрівання реакційної суміші, то dH = CP dT, тоді
G
=
H
- T
=
H
- T·Cp·Ln·
Коли ентальпія з ході процесу не змінюється (7#= о), то рівняння приймає вигляд:
G
= RTL·
= RTL·