2. Перший закон термодинаміки і газові процеси

2.1 Основні залежності, формули та рівняння

Перший закон термодинаміки в математичному виді можливо виразити так: все підведене тепло до газу в процесі витрачається на зміну внутрішньої енергії і на удосконалення роботи.

Рівняння першого термодинаміки застосовується в двох видах:

Перший вид:

d_q = dU + A·P·D_v

q = U + A·L

(2.1)

де:

U - зміна внутрішньої енергії газу при С_р = const

L - робота процесу, кДж\кг

Другий вид:

d_q = J - А·V·dР

q = j – А V·dР = J + A·L₀

(2.2)

де

VJ - зміна ентальпії газу при C_р= const

Lo - робота, кДж/кг .Ентальпія і внутрішня енергія мають слідуючий взаємозв'язок:

J=U + A.P. V (2.3)

де

Р - тиск газу, Па

V - питомий об’єм газу, м³\кг

Ізобаричний процес:

В ізобаричному процесі тепло, надане газу, іде на збільшення його ентальпії:

q-Aj-Bp(t2-t1)

Робота з ізобарному процесі визначається по формулі:

L = Р (V₂ – V1)

Ізохорний процес:

Тепло, яке надане газу, іде на збільшення його внутрішньої енергії

q = U = С_V·(t₂ – t₁) (2.4)

Робота з ізохорному процесі

L=0

Ізотермічний процес:

В цьому процесі тиск газу зворотно пропорціональний його об’ємам:

P2/P1=V1/V2

Тепло, надане ідеальному газу, іде на виконання роботи:

q = AL = AP1V1 LnV2/V1

Зміна знутрішньої енергії і ентальпії дорівнюють нулю

Робота визначається по формулі:

L = Р₁V₁Ln = Р₁V₁Ln

Адіабатний процес:

Для адіабатних процесів dq = 0. Робота газу складає:

L = ·(Р₁V₁ – Р₂V₂) = ·(Т₁ – Т₂) = =

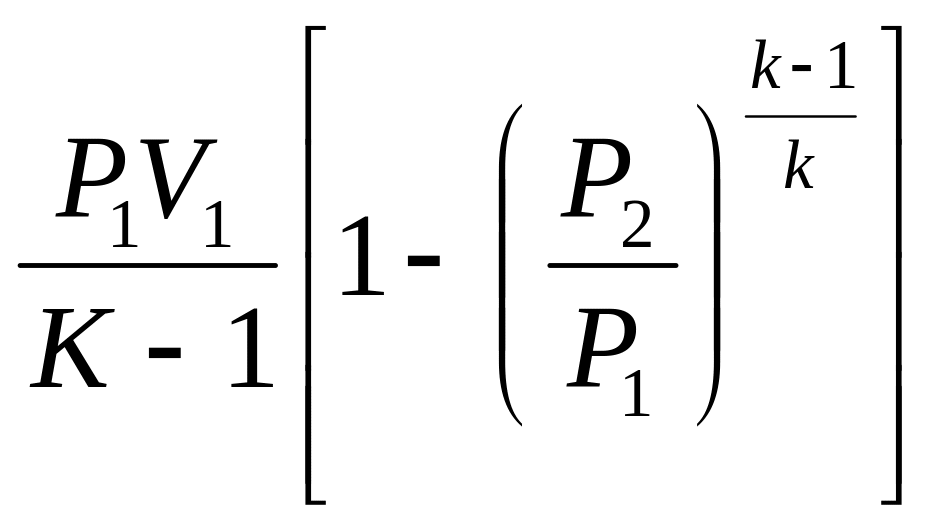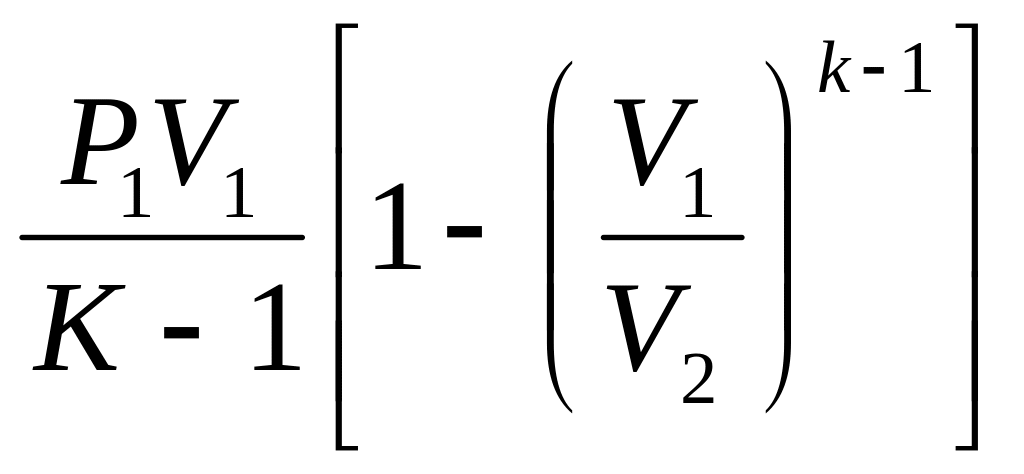
В адіабатному процесі робота впроваджується за рахунок зменшення внутрішньої енергії газу:

L = ·(U - U) = ·С_V·(t₁ – t₂)

Політропний процес:

Роботу газу в політропному процесі визначають по формулі:

L = ·(Р₁V₁ – Р₂V₂)

або

L = ·(Т₁ – Т₂)

L =

Зміна внутрішньої енергії газу і тепло з політропному процесі знаходиться по формулі:

U = U₂ – U₁ = С_V·(t₂ – t₁)

q = С_V - ·(t₂ – t₁)

Показник політропи

n = . . . mа . . . n =

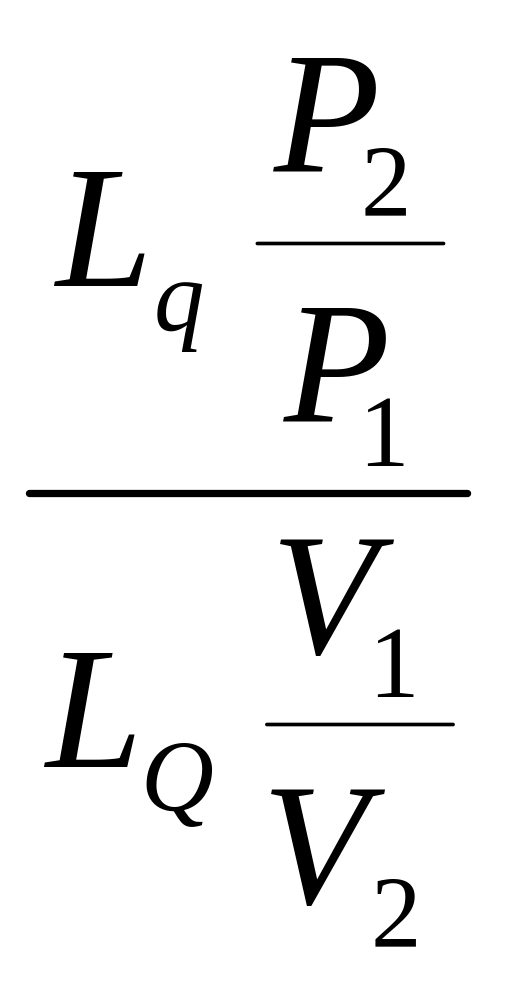
2.2 Приклади розрахунків

Приклад 1

Визначити об’єм балону для стиснення азоту та його вагу, якщо об’єм посудини з горючим - V_R= 0.25 м³ ,а об’єм посудини для окислення V₀ = 0.5 м³. Тиск подачі компонентів Р_к = 2.0 мПа, тиск азоту в балоні Р₀ =30мПа і температура - 30°С. Вирішення

1. Процес - ізотермічний. Рівняння ізотерми PV = const для даної задачі буде мати вигляд:

P_n2·V_n2 = P_к(V_r+V₀+V_N2)

Після підстановки величин і відповідної перебудови рівняння одержимо:

15 = 0,75 + V_n2

звідки

V_N2 =0,75/14= 0.0536л³

Таким чином, об’єм балону для стиснення азоту складає 0.0536 м³

2. Вагу стисненого азоту (в кг) визначимо із рівняння стану для G кг речовини, яке для прийнятих відзначень буде мати вигляд:

РN₂·VN₂ = GN₂·RN₂·ТN₂

звідки

GN₂ =

RN₂ - газова постійна для азоту;

RN₂ =

RN₂ = = 30,3 кг.м/кг.град.

Rm - універсальна газова постійна, яка дорівнєю 848;

М_Н2- молекулярна вага азоту, М = 28;

Т - абсолютна температура азоту

GN₂ = = 18,1 кг

Визначемо масу стисненого азоту (т_а) в системі СІ Рівняння стану для m кг речовини має вигляд:

Р_N2V = mRT

де

Раб - абсолютний тиск, н\м² .

V- об’єм м³

m - маса, кг

Т - абсолютна температура, К

R - газова постійна, яка має розмірність

R =

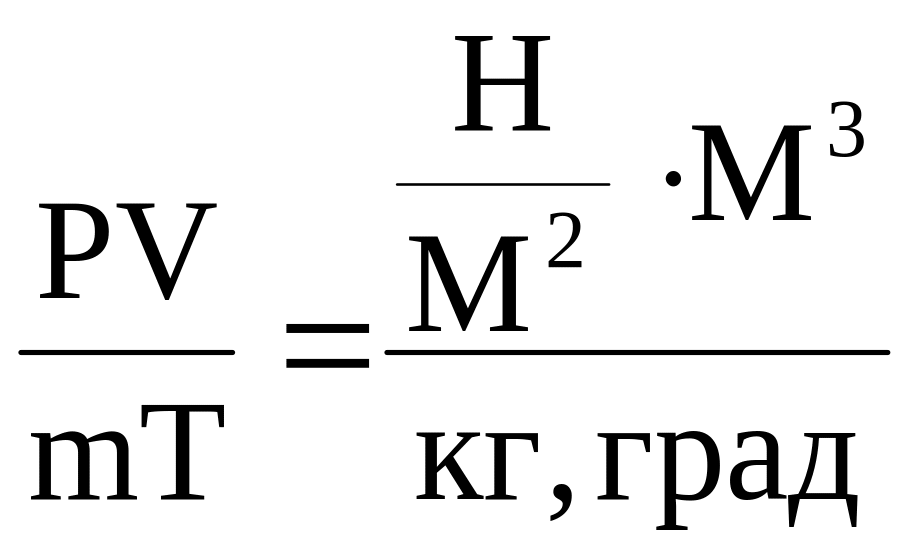
або

R =

Залишимо для данної задачі:

Р_N2V_A=m_N2.R_N2.T_N2

де

R_a- газова постійна азоту,

Т_N2=20+ 173= 193 К

Газову постійну R_N2 визначимо із рівняння

R_N2 =

де R - універсальна газова постійна

R = 848. 9,81 = 8.32.10³ Дж/кмольград

М_N2=28, тоді

R_N2 =8,31/28=0,297·10³Дж/кмольград

Визначаємо масу стисненого азоту

m_а = ; m_а = = 18,1 кг

В системі СІ Р_а дорівнює:

Ра = 300 кг/см³= 300.10⁴ кг\м². 9.81 = 294.3.10⁵ н\м²

Приклад 2

Ізотермічно стискують 1000 м³ азоту від 100 до 500 кн\м²Температура азоту 127°С

Підрахувати:

а) об’єм азоту після стиснення;

б) роботу, що витрачена на стиснення;

в) кількість тепла, що виділяється.

Розв’язок

1. Визначимо об’єм азоту після стиснення:

V₂ = ; V₂ = м³

2. Робота стиснення визначається по формулі:

А = 19. 1. п. Т. Ld·

де п - кількість азоту, яка визначається по формулі:

Тоді

n = n = = 30,0 кмоль

А = 191,1·30·400·Lg· = - 168 кДж

3. Кількість тепла, яке зиділяється системою буде 168 мДж

Приклад З

Визначити показник політропи, кількість відведеного тепла, середню теплоємність процесу, зміну внутрішньої енергії і витрачену роботу, якщо в результаті стиснення 24 м³ повітря від Рі = 2 атм або 0.098 мПа до Р₂ = 10 атм або 0.98 мПа, об’єм його зріс в 6 раз. Газова постійна для повітря R = 29.3 кг.м\кг.град, показник адіабати - К= 1.41, теплоємність повітря С_р = 0.24 ккал\кг.град. І C_v= 0/17 ккал\кг .град.

Рішення

1. Показник політропи стиснення визначається по формулі:

n =

Підставляємо числові значення, одержуємо:

n = = = 1,29

2. Витрачена на стиснення повітря робота дорівнює:

L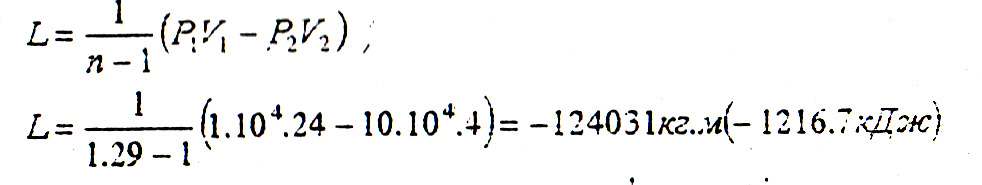 = ·(Р₁V₁ – Р₂V₂)

L = ·(1·10⁴·24 – 10·10⁴·4) = - 124031кг.м (-1216,7 кДж)

3. Кількість підведеного тепла визначається по формулі:

q = U + АL

= = = = х = = - 2,42

q = q = = - 368 кДж

4. Зміна внутрішньої енергії розраховується по формулі:

U = q - АL

U = - 88,0 + = 202 ккал = 846 кДж

4. Середня теплоємність процесу дорівнює:

С = С_V· = 0,17· = - 0,082 ккал/кг.град

або С = - 0,343 кДж\кг.град

Приклад 4

В автоклаві знаходиться 20 дм³ водню під тиском 120 кн\м² і температурі 17°С. При нагріванні автоклава тиск в ньому підвищується до

600 кн\м² Підрахувати:

а) скільки тепла підведено водню, в автоклаві, якщо мольна теплоємність його при постійному об’ємі складає C_v = 20.93 Дж\моль;

б) де якої температури нагрівається водень?

Розв'язок

1. Визначаємо кількість тепла, яке отримує водень по формулі:

V = cоnst – ізохорний процес

q = n·С_V·(t₂ – t₁)

q = n· ·(Р₂ – Р₁)

де

п - число молей водню:

Р1Т1 - початковий стан газу;

Р₂Т₂- кінцевий стан газу

2. Розрахуємо кількість водню:

n = = = 1,02·10^-3 кмоль

q = ·(600 - 120) = 24,3 кДж

3, Визначаємо температуру водню після нагрівання:

q = n·С_V·(t₂ – t₁)

24,8 = 1,02·10^-3·20.93·(Т₂ - 290)

Т₂ = 1450 К або 1177 °С

Приклад 5

В циліндрі з поршнем знаходиться повітря, його тиск 4 ат, температура - г= 500°С Від повітря віднімається тепло таким чином, що в кінці процесу установлюється температура 100°С. Об’єм циліндра, в якому знаходиться повітря, 200 л

Визначити кількість відведеного тепла, кінцевий об’єм, зміну внутрішньої енергії та звершену над газом роботу стиснення.

Рішення

1. Кількість віднятого тепла визначається по рівнянню:

q_g = V_Н·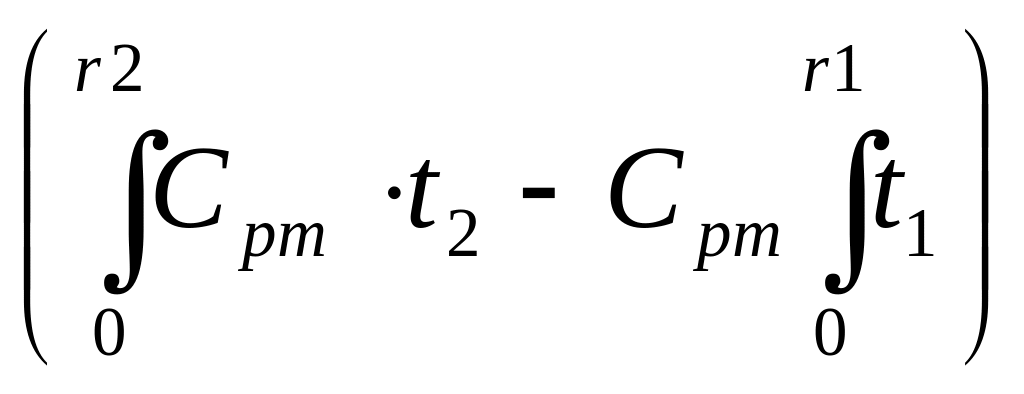

а) Об’єм газу відносимо до нормальних умов по формулі:

V_Н = = = 0,342 м³

б) знаходимо значення середньої теплоємності повітря по табл. 1 -7 \ \ для t1=500 і t₂ = 100 °С

Срм = 1.2866 + 0.0001201 (100 + 500) = 1.368 кДж\м³ град.

Підставляємо знайдені значення в формулі для визначення кількості тепла:

Q_B= 0.342 . 1.368 (100 - 500) = - 186 кДж

2. Кінцевий об’єм визначається по закону Гей-Люсака:

V₂ = V₁· ; V₂ = м³

3. Зміна внутрішньої енергії:

U = V_Н·С_р·(t₂ – t₁)

U = 0,342·(0,9157 + 0,0001201·600)·х·(100 - 500) = - 135,4 кДж

або на основі формули:

q_V = U_V = (U₂ – U₁)

тобто це рівняння першого закону термодинаміки при V=const розраховуємо зміну внутрішньої енергії, користуючись таблицями додатку:

U_V = 0,342·(345 – 738) = - 135 кДж;

= U₂·β_Н = 266·71,293 = 345 кДж/м³;

= U₁·β_Н = 570:5·1,293 = 738 кДж/м³;

Значення U₂ і Ui для температур t₂ = 100°С і t1 = 500°С взяті із додатку

4. Робота, яка створена над газом, дорівнює:

Q = P(V₂-V₁)

Q = 5. 0,0981.10⁶ (0.0966 - 0.2) = - 50.6 кДж

Перевірка по рівнянню першого закону термодинаміки:

Q_B= YU + W; - 186 = - 135.4-50.6 = - 186 кДж

та аргону SN2 ⁼ 0,37; S_Ar = 0,63. Гази ідеальні. Ентропія азоту та аргону дорівнює нулю при параметрах Р₂ — 1 кг/см"; t = 0 °С. Використовують табл. 8.

Ентропія суміші дорівнює сумі ентропій газів та ентропії зміщення,

1. Ентропія 0,37 кг азоту на 1 кг суміші визначається по формулі:

SN₂ = (S₂ - S₁ – R·ln )·qN₂

SN₂ = (0,1854 - 0 - ·2,3·lq3)·0,37 = 0,0398·4,2 = 0,167 кДж/кг·град

2. Ентропія 0,63 кг/кг суміші аргону дорівнює:

S_Аr = (С_р·ln – R·ln )·q_Аr

S_Аr = ( ·lq - ·lq3)·0,63·2,3 = 0,0236 ккал/кг·град =

= 0,099 кДж/кг·град

3.Ентропія змішення розраховується по формулі:

ΔS = q_Аr·R_Аr·ln· + qN₂·RN₂·ln· ,

ΔS = 0,63· ·2,3·lq· + 0,37· ·2,3·lq· = 0,0452 ккал/кг·град =

= 0,189 кДж/кг·град

4 .Ентропія 1 кг суміші при заданих параметрах дорівнює:

S=S_N2 + S_Ar + ΔS

S = 0.0398+0.0236+0.0452 = 0.1086ккал/кг * град = 0,456кДж./ кг * град

Приклад 2

Розрахувати зміну ентропії при переході 1 кг води, взятої при температур 25 °С, в стан перегрітої пари з t = 200 °С при нормальному тиску, при цьому:

а) теплоємність води становить 4,2 кДж/кг град, яка не залежить від

температури;

б) середня мольна теплоємність в межах температур 100-200"С дорівнює-

33.8 кДж/кмоль град;

в) теплота випарювання води - 2260 кДж/кг

Розв'язок

1 .Зміна ентропії (ДЛ')системи (1 варіант), визначається, як сума трьох величин

ΔS = ΔS₁ + ΔS₂ + ΔS₃

де ΔS₁ – зміна ентропії води при нагріванні її від 25 °С до 100 °С ;

ΔS₂ – зміна ентропії при переході води із рідини в пару;

ΔS₃ – зміна ентропії при перегріванні водяної пари до 200 °С ;

Розв’язок

1. Зміна ентропії (VS) системи І варіант, визначається, як сума трьох величин:

S = S₁ + S₂ + S₃

де S₁ – зміна ентропії води при нагріванні її від 25 °С до 100 °С ;

S₂ – зміна ентропії при переході води із рідини в пару;

S₃ – зміна ентропії при перегріванні водяної пари до 200 °С ;

а) S₁ = = С_р·2,3 lq· ;

S₁ = = 4,2·2,3 lq· = 0,94 кДж/кг;

б) S₂ =

S₂ = = 6,06 кДж/кг;

в) S₃ = = С_р·2,3·lq· = 33.8.2,3·lq·1.268 = 8 кДж/кмоль =

= = 0,44 кДж/кг ;

S = 0,94 + 6,06 + 0,44 = 7,44 кДж/кг

Другий варіант

Величину зміни ентропії можливо підрахувати по таблицях [ ].

Для води в пароподібному стані

Для води в рідинному вигляді

Тоді

S⁰ = 189 – 70 = 119 кДж/кмоль

або

S⁰ = = 6,61 кДж/кг

До цієї величини добавимо VS₃ із попереднього розрахунку:

S⁰ = 6,61 + 0,44 = 7,05 кДж/кг

Приклад З

Розрахувати ентальпію суміші газів віднесену до 1НМ³ при температурі t=800°c"

Димові гази мають склад, %:

С0₂= 16.1; 0 = 7.5; N₂ = 76.4

Розрахунок

1. Визначаємо ентальпію суміші газів, ентальпію компонентів знаходимо по таблицях [ ].

І_сум. = RСО₂·ІСО₂ + RО₂·ІО₂ + RN₂·ІN₂

ісум. = 0,161.207,4 + 0,075.194,1 + 0,764.207,9 = 208,2 ккал/кг = 872 кДж\кг

2. Розраховуємо ентальпію в кДж\НМ³

І_сум. = І·Р см

Р_сум. =

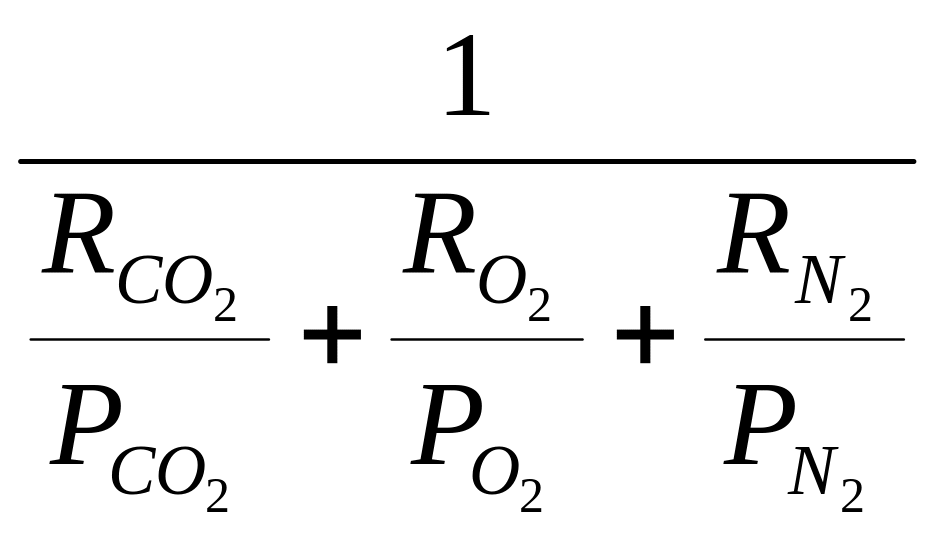
Р_сум. = 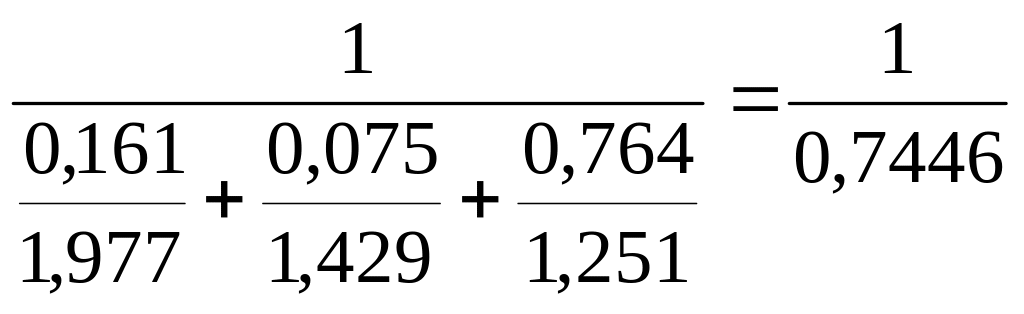= 1,343 кг/нм³

Тоді

І_сум. = 87,2·1,343 = 1171 кДж/нм³