§ 1.8 Связь между потенциалом и напряженностью. Эквипотенциальные поверхности

Электрическое поле описывают с помощью векторной величины , или с помощью скалярной величины j. Между ними существует связь. Например, работа при перемещении заряда в электростатическом поле

dA = - dW_П = qdj,

, dA = Fd cosa, , ,

dA = qEdr, значит - qEdr = qdj, E =- dj / dr. (1.21)

, , , .

Покажем, что изменение потенциала вдоль силовой линии максимально. Напряженность поля вдоль произвольного направления равна: , где угол a это угол между векторами и . С другой стороны т.к. cosa < 1, то при cos a = 1. Tо есть, в направлении силовой линии значение вектора напряженности , а значит и величина в этом направлении, будет максимальной. Знак минус указывает на то, что вектор направлен в сторону наиболее быстрого убывания потенциала. Из уравнения (1.21) следует, что напряженность поля численно равна скорости изменения потенциала вдоль силовой линии. На основании формулы (1.21) видно, что единицей измерения Е является вольт/метр (В/м).

Э лектростатическое поле можно изображать при помощи эквипотенциальных поверхностей (рисунок 1.16). ЭКВИПОТЕНЦИАЛЬНАЯ ПОВЕРХНОСТЬ - геометрическое место точек с одинаковым потенциалом. Вокруг каждой системы зарядов можно провести бесконечное множество эквипотенциальных поверхностей. Обычно их проводят таким образом, чтобы разность потенциалов между двумя соседними эквипотенциальными поверхностями была одинакова. Зная расположение силовых линий поля, можно построить эквипотенциальную поверхность, и наоборот. Эквипотенциальную поверхность проводят всегда перпендикулярно линиям Е. Эквипотенциальная поверхность по определению j = const, значит =0 вдоль поверхности, то есть = =Ecosa = 0, значит cos a = 0, т.е. a = 90⁰.

§ 1.9 Вычисление потенциала некоторых простых полей

1. Поле точечного заряда

, , dj = -Edr, , .

2. Поле, создаваемое, бесконечной равномерно заряженной плоскостью

, dj = -Edr = -sdr/(2ee₀), .

3. Электростатическое поле между двумя параллельными бесконечными плоскостями, заряженными равномерно и разноименно

, dj = Edх, ,

где d - расстояние между обкладками конденсатора.

4. Электростатическое поле бесконечного равномерно заряженного цилиндра

, dj = -Edr, .

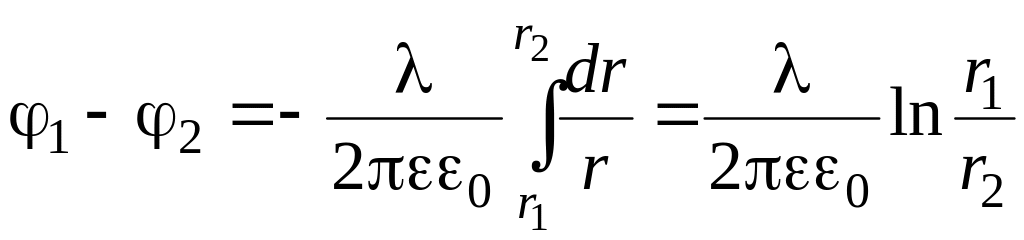Разность потенциалов между обкладками цилиндрического конденсатора

.

5. Электростатическое поле равномерно заряженной сферической поверхности

, dj = -Edr, .

Положив r₁ = R, а r₂=¥ найдем потенциал заряженной сферической поверхности

.

6. Электростатическое поле равномерно заряженного шара по объему

, dj = -Edr, , .

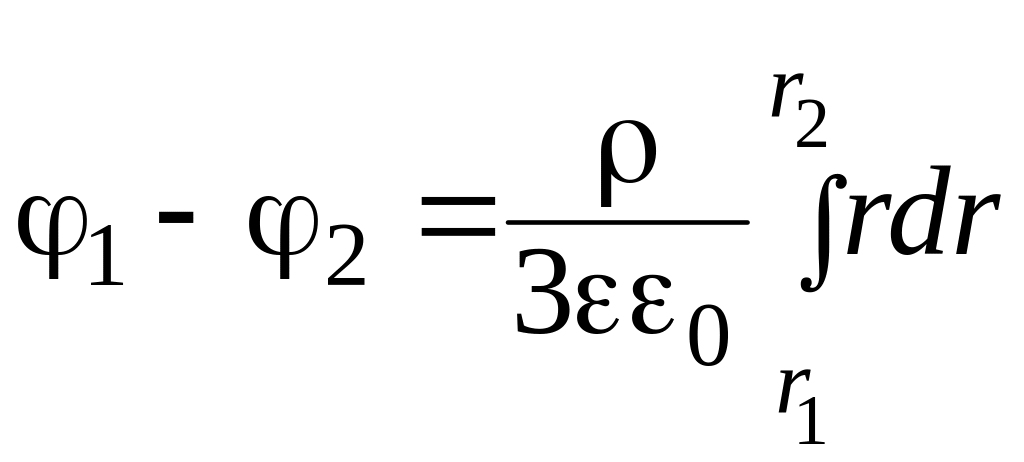Формула пригодна для вычисления разности потенциалов внутри шара.

При r₂ = R, r₁ =¥ найдем потенциал шара

.

Для определения разности потенциалов вне шара

, dj = -Edr, .

§ 1.11 Электрическая емкость

Сообщенный проводнику заряд распределяется по поверхности так, что напряженность поля внутри проводника равна нулю. Если проводнику, имеющему заряд, сообщить еще заряд, то второй заряд должен распределиться так же, как и первый, иначе поле в проводнике не будет равно нулю. Это справедливо в случае, если увеличение заряда на проводнике не вызовет изменения зарядов на окружающих телах. Отношение плотности заряда в двух точках поверхности проводника при любой величине заряда будет одинаково. Отсюда вытекает, что потенциал уединенного проводника пропорционален находящемуся на нем заряду. Действительно, увеличение в несколько раз заряда приводит к увеличению в то же число раз напряженности поля в каждой точке окружающего проводник пространства. Следовательно, в такое же число раз возрастет работа переноса по любому пути единичного заряда из бесконечности на поверхность проводника, т.е. потенциал проводника. Таким образом, для уединенного проводника

q = Cj. (1.22)

Коэффициент пропорциональности C называется электроемкостью или просто емкостью проводника. Из уравнения (1.22) следует, что

С = q/j, (1.23)

емкость численно равна заряду, сообщение которого проводнику повышает его потенциал на единицу. В системе СИ электроемкость измеряется в фарадах. Одна фарада - это емкость такого проводника, которому сообщают заряд в 1 Кл, а его потенциал при этом возрастает на 1 В.

Фарада это очень крупная единица емкости, поэтому на практике используются более мелкие единицы - микрофарада и пикофарада (10-6 и 10-12 Ф).