§ 1.4 Принцип суперпозиции

Если электрическое поле создается несколькими зарядами, то сила, с которой эти заряды действуют на некоторый пробный заряд, равна векторной сумме сил, с которыми действует на данный заряд каждый из зарядов системы. ПРИНЦИП СУПЕРПОЗИЦИИ: напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности

.

Принцип суперпозиции позволяет вычислить напряженность поля любой системы зарядов. Разбив протяженный заряд на достаточно малые заряды величиной dq, любую систему зарядов можно свести к совокупности точечных зарядов.

Определим напряженность электрического поля диполя, исходя из принципа суперпозиции. Электрический диполь - система двух равных по величине и противоположных по знаку электрических зарядов +q и -q, расстояние ℓ между которыми мало по сравнению с расстоянием до рассматриваемых точек, где этот диполь создает поле.

Плечом диполя называется вектор , направленный по оси диполя от (-q) к (+q) и равный расстоянию между ними. Электрическим моментом диполя называется произведение положительного заряда диполя на плечо

.

В соответствии с принципом суперпозиции полей напряженность , созданная диполем в произвольной точке поля, равна .

Пример 1. Найдем напряженность электрического поля в точке А, лежащей на линии, совпадающей с продолжением плеча диполя на расстоянии r от центра плеча диполя (рисунок 1.2), используя принцип суперпозиции

,

где

.

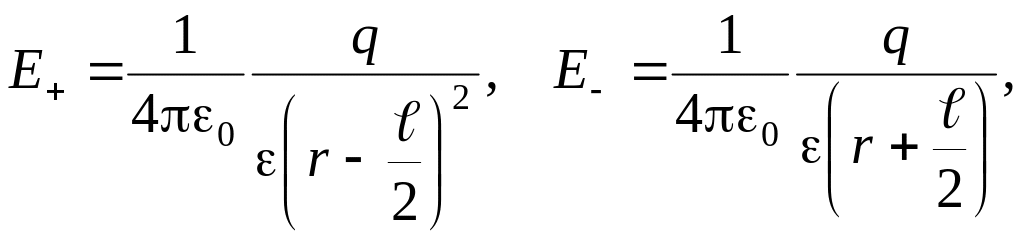
е сли то . (1.6)

Пример 2. Найдем выражение для напряженности поля диполя в точке А, расположенной на перпендикуляре, восстановленном к оси диполя из его середины (рисунок 1.3).

В этом случае ,

,

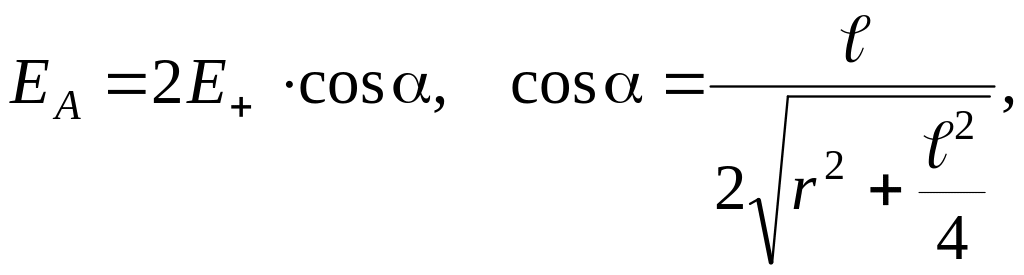
, если , то получим

. (1.7)

П ример 3. Найдем выражение для напряженности электрического поля, создаваемого диполем в точке А, находящейся на расстоянии r от центра диполя, если радиус вектор r составляет с плечом диполя угол a (рисунок 1.4).

Из точки +q восстановим перпендикуляр на радиус вектор и поместим в точку пересечения заряд величиной (±q). В результате получили два диполя. Напряженность поля, созданного первым диполем, вычисляется по формуле (1.6), как в случае 1. Напряженность поля, созданного вторым диполем, вычисляется по формуле (1.7), как в случае 2. Поле, созданное первым диполем:

.

Поле, создаваемое вторым диполем: .

Будем считать, что и r₁=r₂, где r, r₁ и r₂ - расстояния от реального диполя и двух вспомогательных соответственно

_. (1.8)

Формула (1.8) является расчетной.

§ 1.5 Графическое изображение электростатических полей. Поток вектора напряженности

Электрические поля иногда необходимо изображать графически, однако это делать при помощи векторов напряженности не очень удобно и наглядно. Вектора напряженности при этом накладываются друг на друга, и получается весьма запутанная картина. Рисунок получается более простой и понятный, если для его построения использовать силовые линии. Силовые линии - кривые, касательные к которым в каждой точке поля совпадают с направлением вектора напряженности поля в этой точке.

Свойства силовых линий:

1 . Силовые линии электростатического поля начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. Силовые линии точечного заряда представляют собой совокупность радиальных прямых, направленных от заряда, если он положительный, и к заряду, если он отрицательный, т. е. одним концом они упираются в заряд, а другим уходят в бесконечность (рисунок 1.5).

2. Силовые линии электростатического поля никогда не пересекаются: в самом деле, полное число N силовых линий, пересекающих сферическую поверхность произвольного радиуса r, будет равно произведению густоты линий на площадь поверхности сферы 4p×r². Густота линий определяется по формуле

,

следовательно,

,

т.е. число силовых линий на любом расстоянии от заряда будет одно и то же. Отсюда и вытекает, что силовые линии нигде, кроме зарядов, не начинаются и не заканчиваются.

3. Густота силовых линий пропорциональна вектору напряженности, т.е. густота силовых линий выбирается так, что количество линий, пронизывающих единицу поверхности перпендикулярной к линиям, было равно численному значению вектора напряженности. Если электрическое поле на рисунке изображается рядом параллельных прямых, равноотстоящих друг от друга, то такое поле является однородным (например, поле между обкладками заряженного конденсатора).

Поскольку густота линий выбирается равной численному значению напряженности, то количество линий, пронизывающих площадку dS, перпендикулярную к вектору , будет численно равно ЕdS. Если площадка dS ориентирована так, что нормаль к ней образует с вектором угол a, то количество силовых линий, пронизывающих площадку dS, будет численно равно E dS cosa = E_n dS, где E_n - составляющая вектора по направлению нормали к площадке. Отсюда для количества линий Е, пронизывающих произвольную поверхность, получается следующее выражение

. (1.9)

Если имеется поле некоторого вектора , то выражение

,

называется потоком вектора через площадку S. Поэтому выражение (1.9) представляет собой поток вектора напряженности электрического поля через площадку S.

В случае замкнутой поверхности (рисунок 1.6) принято вычислять поток, выходящий из охватываемой поверхностью области наружу. Соответственно под нормалью к площадке в дальнейшем будем всегда подразумевать обращенную наружу, т.е. внешнюю нормаль. Поэтому в тех местах, где вектор направлен наружу (т.е. линии выходят из объема, охватываемого поверхностью), Е_n и соответственно dN будут положительными, в тех же местах, где вектор направлен внутрь (т.е. линии входят в объем, охватываемый поверхностью), Е_n и dN будут отрицательными.