Уточняющая таблица
Параметры |
XI |
Х2 |
Х3 |
Х4 |
|
XI |
1 |
2 |
1,6 |
2 |
6,6 |
X2 |
0 |
1 |
0,2 |
1,4 |
2,6 |
Х3 |
0,4 |
1,8 |
1 |
2 |
5,2 |
Х4 |
0 |
0,6 |
0 |
1 |
1,6 |
Вариант 3. Использование экспертной оценки на основе правила среднего арифметического.
Таблица 4
Распределение экспертных оценок на основе правила среднего арифметического
1 эксперт |
2 эксперт |
3 эксперт |
4 эксперт |
5 эксперт |
5 |
4 |
3 |
5 |
4 |
Формула коэффициента вариации:
где: d — показатель дисперсии, получаем:
Xср = 1/5(5+4+3+5+4) = 4,2
dx2 = (1/(5–1))[(5–4,2)2+(4–4,2)2+(3–4,2)2+(5–4,2)2+(4–4,2)2] = 2,8/4 = 0,7
Вариант 4. Использование экспертной оценки с учетом коэффициента конкордации.
Таблица 5
Экспертная оценка с учетом коэффициента тесноты связей
Исследуемые факторы |
Эксперты |
Сумма рангов по каждому признаку |
Отклонение суммы рангов от средней суммы - Аj |
Квадрат Отклонения суммы (Аj 2) |
||||
1 |
2 |
3 |
4 |
5 |
||||
XI |
1 |
1 |
1 |
1 |
1 |
5 |
-7,5 |
56,2 |
Х2 |
2 |
2 |
2 |
2 |
3 |
11 |
-1,5 |
2,25 |
Х3 |
3 |
3 |
3 |
3 |
2 |
14 |
1,5 |
2,25 |
Х4 |
4 |
4 |
4 |
4 |
4 |
20 |
7,5 |
56,2 |
Итого |
|
|
|
|
|
50 |
Тj= 0 |
116,9 |
Формула коэффициента конкордации:
,
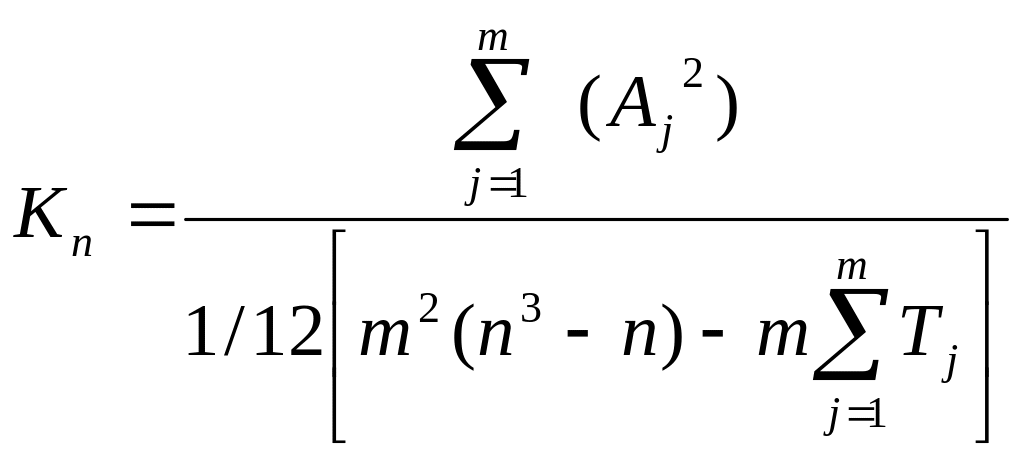где: j – оцениваемый параметр (фактор);
∑(A2) – сумма квадратов отклонения суммы рангов от средней суммы;
п – количество экспертов;
т – количество рассматриваемых параметров;
Tj – сумма отклонений суммы рангов от средней суммы.
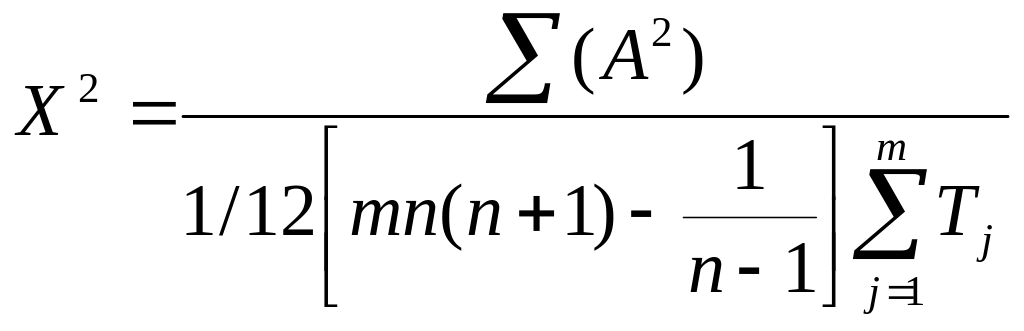
Таблица 6
Критические значения показателя x2
m |
n |
|||
|
3 |
4 |
5 |
6 |
3 |
5,7 |
7,1 |
8,1 |
9,7 |
5 |
6,2 |
7,5 |
8,9 |
10,4 |
Формула коэффициента тесноты связей:
Вариант 5. Использование экспертной оценки на основе качественного отбора.
Таблица 7
Экспертная оценка на основе качественного отбора
Эксперты |
Альтернатива 1 |
Альтернатива 2 |
Альтернатива 3 |
Альтернатива 4 |
||||||||
Р |
Б |
П |
Р |
Б |
П |
Р |
Б |
П |
Р |
Б |
П |
|
А |
4 |
7 |
28 |
3 |
8 |
24 |
2 |
4 |
8 |
3 |
4 |
12 |
В |
3 |
2 |
6 |
3 |
7 |
21 |
3 |
4 |
12 |
4 |
4 |
16 |
С |
5 |
6 |
30 |
3 |
6 |
18 |
2 |
4 |
8 |
3 |
6 |
18 |
Итого |
|
64 |
|
63 |
|
28 |
|
46 |
||||
Р – ранг альтернативы (по 5-балльной шкале);
Б – балл (степень возможности реализации данной альтернативы);
П – произведение Р и Б.
Вариант 6. Метод дельфийского совещания (метода Турофа): попарное сравнение объектов оценки.
Таблица 8
Схема попарного сравнения объектов оценки па методу Турофа
|
А |
В |
С |
D |
∑а |
∑а2 |
А |
|
1 |
0 |
1 |
2 |
4 |
В |
0 |
|
1 |
0 |
1 |
1 |
С |
1 |
0 |
|
1 |
2 |
4 |
D |
0 |
1 |
0 |
|
1 |
1 |
Итого |
|
|
|
|
6 |
10 |
Общая оценка по каждому эксперту проводится по формуле:
а – результат сравнения экспертом двух объектов
