6. Уравнение Бернулли для потока реальной жидкости

При течении реальной жидкости между ее слоями возникает трение, что приводит к существенной нерав­номерности распределения скоростей по сечению потока, а также к потерям энергии при перемещении жидко­сти от одного сечения к другому (рис. 14).

Рис. 14. Графическая иллюстрация уравнения Бернулли для потока реальной жидкости

Уравнение Бернулли для потока реальной (вязкой) жидкости будет иметь следующий вид:

где — коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечению потока;

— суммарные потери полного напора (гидравлические потери).

Коэффициент Кориолиса представляет собой отношение действительной кинетической энергии потока в данном сечении к кинетической энергии того же потока и в том же сечении, но при равномерном распределе­нии скоростей. При равномерном распределении скоростей (поток идеальной жидкости) =1, а в потоках ре­альной жидкости коэффициент Кориолиса обычно лежит в пределах 1÷2.

Величина потерь напора (удельной энергии) определяется многими факторами: площадью поперечного сечения и длиной трубопровода, шероховатостью его внутренней поверхности, наличием местных сопротив­лений, скоростью и режимом течения, вязкостью жидкости.

* Реально существующим в потоке является только гидромеханическое давление р, две другие величины на­зываются давлениями условно.

Потери энергии при течении жидкости принято делить на две группы: потери на трение по длине h_тр и мест­ные потери h_м (рис. 15).

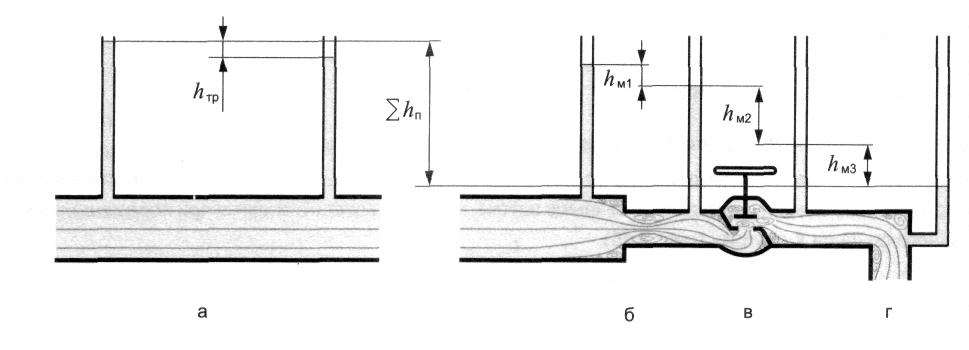
Рис. 15, Гидравлические потери по длине (а) и местные (б, в, г)

Потери на трение по длине h_тр — это потери энергии, которые в чистом виде возникают в прямых трубах постоянного сечения, т.е. при равномерном течении, и возрастают пропорционально длине трубы. Данные по­тери обусловлены не только трением жидкости о стенки канала, но и трением слоев жидкости между собой, а потому имеют место не только в шероховатых, но и в гладких трубах.

Местные потери h_м — это потери в местных (локальных) гидравлических сопротивлениях, вызывающих деформацию потока, изменение его скорости и вихреобразование.

Суммарная потеря полного напора на участке между начальным и конечным сечениями складывается из потерь удельной энергии во всех гидравлических сопротивлениях, расположенных на рассматриваемом уча­стке потока.

7. Режимы течения жидкости

Экспериментальные исследования потоков реальной жидкости показывают, что процессы, происходящие в них, существенно зависят от характера течения. Различают два режима течения жидкостей: ламинарный (рис. 2.17, а) и турбулентный (рис. 2.17, б).

Рис. 16. Эпюры скоростей при ламинарном (а) и турбулентном (б) режимах течения жидкости

Ламинарное течение характеризуется упорядоченным (слоистым) движением без перемешивания частиц жидкости и без пульсаций скоростей и давлений. Когда скорость движения превысит некоторую критическую величину, слои начинают перемешиваться, образуются вихри; течение становится турбулентным, возрастают потери энергии.

При течении жидкости по трубопроводу переход от ламинарного режима к турбулентному наблюдается в тот момент, когда осредненная по сечению трубы скорость движения потока становится равной критической лак показывает эксперимент, критическая скорость прямо пропорциональна кинематической вязкости v жидкости и обратно пропорциональна внутреннему диаметру d трубы:

где k — коэффициент пропорциональности;

v - кинематическая вязкость жидкости, м²/с;

d - внутренний диаметр трубы, м.

Экспериментально был установлен и тот факт, что смена режима течения любой жидкости по трубе любого диаметра имеет место лишь при определенном значении безразмерного коэффициента k. Данный коэффициент называют критическим числом Рейнольдса:

Для труб круглого сечения .

Число Рейнольдса используют для описания режима течения:

Значение числа Рейнольдса позволяет судить о характере течения жидкости по трубе:

• ламинарное течение Re < 2 300;

• турбулентное течение Re > 2 300.

Таким образом, зная скорость движения потока, вязкость жидкости и внутренний диаметр трубы, можно найти число Рейнольдса и, сравнив его с величиной , определить режим течения жидкости.

Результаты экспериментов показывают, что сразу после разрушения ламинарного течения устойчивого турбулентного течения еще не появляется. Развитое турбулентное течение устанавливается при Re > 4 000.

Если значение Re уменьшается и оказывается ниже , турбулентное течение не сразу становится ла­минарным. Устойчивое ламинарное течение жидкости снова достигается лишь при значении Re = 0,5

Исходя из того, что законы распределения скоростей по сечению трубы при ламинарном и турбулентном режимах течения жидкости различны, коэффициент Кориолиса, учитывающий неравномерность распределе­ния скоростей в уравнении Бернулли, принимает разные значения:

• для ламинарного течения α= 2;

• для турбулентного течения α = 1.