
- •Федеральное агентство железнодорожного транспорта
- •«Петербургский государственный университет путей сообщения»
- •Насосы, насосные и воздуходувные станции (Конспект лекций) Санкт-Петербург
- •Предисловие
- •Часть I. Насосы и машины для подачи и сжатия воздуха
- •1.1. Назначение насосных и воздуходувных станций в системах
- •1.2. Устройство насосной установки
- •1.3. Классификация насосов. Основные требования к их
- •1.4. Устройство и принцип действия центробежного насоса.
- •1.5. Способы заливки центробежных насосов перед пуском
- •1.6. Основные энергетические параметры насосной установки:
- •1.7. Высота всасывания насоса
- •1.8. Кавитация в насосах. Допустимое значение высоты
- •1.9. Характеристика центробежного насоса
- •1.10. Характеристика системы трубопроводов
- •1.11. Совместная работа насоса и трубопровода. Рабочий режим
- •1.12. Изменения характеристики центробежного насоса при
- •1.13. Перерасчет характеристики насоса с одной частоты вращения рабочего колеса на другую на заданные параметры
- •1.14. Перерасчет характеристики насоса с одного диаметра
- •1.15. Регулирование подачи насоса задвижкой на напорной линии
- •1.16. Регулирование подачи насоса перепуском расхода из
- •1.17. Параллельная работа одинаковых центробежных насосов
- •1.18. Параллельная работа центробежных насосов с разными
- •1.19. Параллельная работа центробежных насосов, расположенных на значительном расстоянии друг от друга
- •1.20. Последовательная работа центробежных насосов
- •1.21. Последовательная работа центробежных насосов, располо-
- •1.22. Кинематика движения жидкости в рабочих органах насоса.
- •1.23. Основное уравнение центробежного насоса. Теоретический
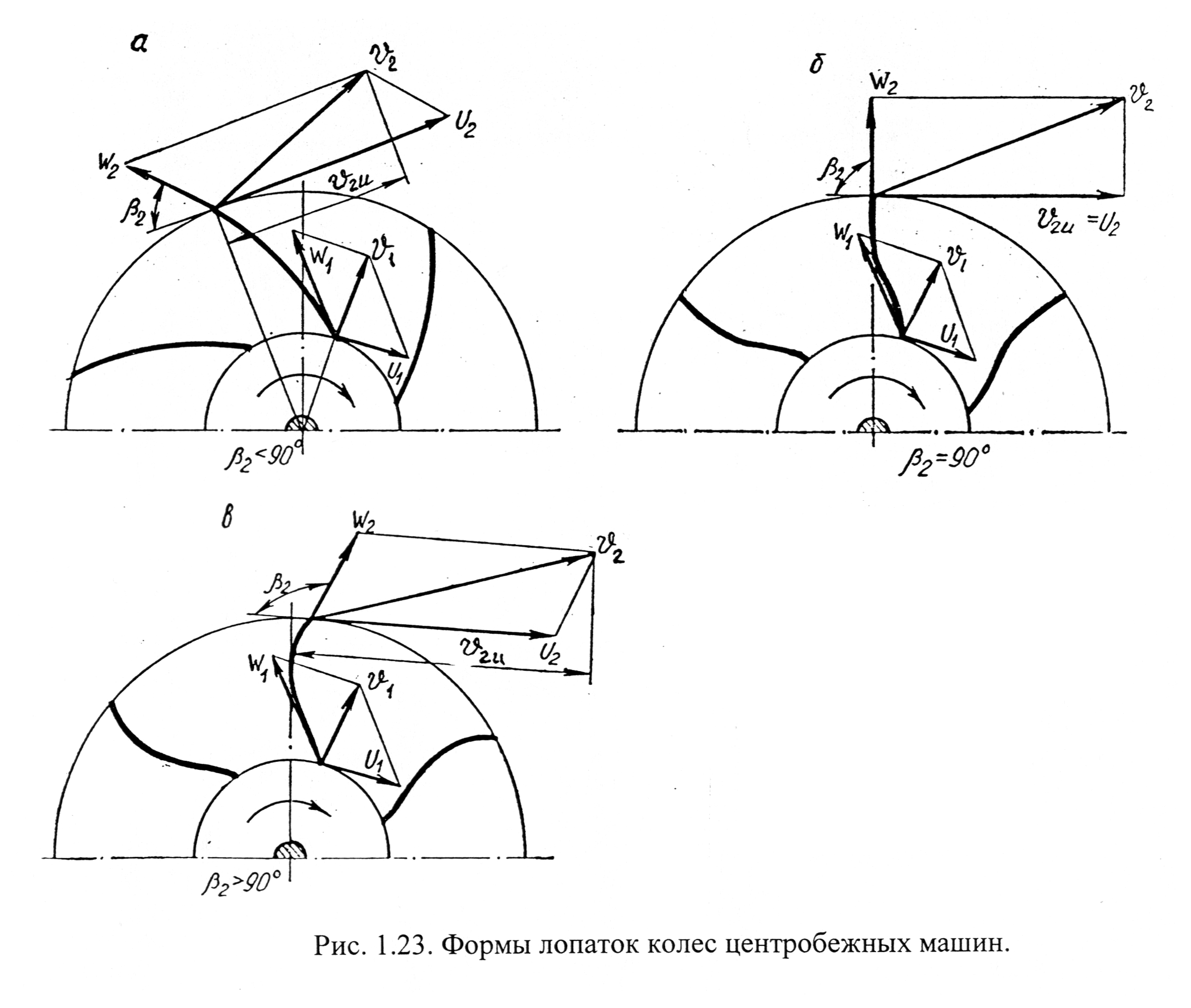
- •1.24. Влияние формы лопаток рабочего колеса насоса на значение теоретического напора
- •1.25. Уравнение теоретической подачи центробежного насоса
- •1.26. Теоретическая характеристика центробежного насоса
- •1.27. Признаки геометрического, кинематического и
- •1.28. Законы подобия насосов
- •1.29. Коэффициент быстроходности для лопастных насосов
- •1.30. Классификация лопастных насосов по коэффициенту
- •1.31. Осевые и диагональные насосы
- •1.32. Вихревые и центробежно-вихревые насосы
- •1.33. Водокольцевые вакуум-насосы
- •1.34. Струйные насосы
- •1.35. Воздушные водоподъемники (эрлифты)
- •1.36. Объемные насосы: поршневые, плунжерные, диафрагменные, насосы-дозаторы
- •1.37. Объемные насосы: винтовые, шестеренные, шиберные,
- •1.38. Вибрационные насосы
- •1.39. Шнековые насосы
- •1.40. Воздуходувные и компрессорные машины: воздуходувки,
- •Контрольные вопросы к части 1 «Насосы и машины для подачи и сжатия воздуха»
- •Часть 2. Насосные и воздуходувные станции
- •2.1. Насосные станции в системах водоснабжения, их назначение и
- •2.2. Схема системы водоснабжения с насосными станциями
- •2.3. Общие рекомендации по проектированию водопроводных
- •2.4. Водопроводные насосные станции первого подъема (внс I) при
- •2.5. Водопроводные насосные станции первого подъема (внс I)
- •2.6. Разновидности водопроводных насосных станций второго
- •2.7. Режим работы внс II
- •2.8. Расчет внс II, подающей воду в водонапорную башню
- •2.9. Высотная схема системы водоснабжения с внс II, подающей воду
- •2.10. Расчет внс II, подающей воду в сеть с контррезервуаром
- •2.11. Высотная схема системы водоснабжения с внс II, подающей воду в сеть с контррезервуаром
- •2.12. Особенности расчета внс II, подающей воду в водопроводную сеть без напорно-регулирующих емкостей
- •2.13. Подбор насосов и анализ их работы в системе водоснабжения
- •2.14. Определение количества резервных агрегатов для водопроводных насосных станций
- •2.15. Требования к устройству и размещению насосных агрегатов
- •2.16. Особенности монтажа всасывающих и напорных трубопроводов
- •2.17. Определение отметки оси насоса и допустимой высоты всасывания.
- •2.18. Оборудование для залива насосов, технического водоснабжения,
- •2.19. Подъемно-транспортное оборудование насосных станций
- •2.20. Проектирование здания насосной станции
- •Схемы и классификация насосных станций систем водоотведения
- •2.22. Насосные станции водоотведения с погружными насосами
- •2.23. Режим работы и категория надежности действия насосных станций водоотведения
- •2.24. Расчет производительности насосной станции водоотведения и
- •2.25. Определение диаметров и устройство всасывающих и
- •2.26. Расчетный напор насосов станции водоотведения
- •2.27. Выбор основных насосов станции водоотведения. Построение
- •- Для аварийного режима работы
- •2.28. Определение количества резервных агрегатов для насосной
- •Резерв насосного оборудования насосных станций водоотведения
- •2.29. Составление высотной и плановой схем насосной станции
- •2.30. Перекачка сырого и сброженного осадков, активного и
- •2.31. Электродвигатели для насосов и их подбор
- •2.32. Электроснабжение насосных станций
- •2.33. Основные понятия об автоматизации работы насосных станций
- •Основные положения по эксплуатации насосной станции
- •2.35. Назначение и состав основного оборудования воздуходувных
- •2.36. Определение необходимого количества воздуха и
- •2.37. Режим совместной работы воздухонагнетателей и воздуховодов
- •2.38. Схемы компоновки внутристанционных воздухопроводов и
- •2.39. Требования к забору и очистке воздуха. Фильтры
- •Контрольные вопросы по курсу «Насосные и воздуходувные станции»
- •Библиографический список
- •Содержание
- •Насосы, насосные и воздуходувные станции
- •190031, СПб., Московский пр., 9
- •190031, СПб., Московский пр., 9
1.23. Основное уравнение центробежного насоса. Теоретический
напор
Напор насоса связан со значением и направлением скоростей потока жидкости в межлопастных каналах рабочего колеса. Поэтому для вывода основного уравнения центробежного насоса – уравнения теоретического напора используют параллелограммы скоростей на входе и выходе жидкости из колеса (см. рис. 1.22), а также теорему об изменении моментов количества движения. Применительно к движению жидкости в каналах рабочего колеса насоса эта теорема формулируется так: прирощение момента количества движения 1 кг массы жидкости за время прохождения межлопастного пространства равно моменту импульсов всех внешних сил, приложенных к потоку от входа в канал до выхода из него за тот же промежуток времени t. Математически теорема записывается следующим образом:
![]() , (1.38)
, (1.38)
где |
|
- момент количества движения на выходе из рабочего колеса насоса; |
|
|
- момент количества движения на входе в рабочее колесо насоса; |
|
|
- момент всех внешних сил относительно оси вращения колеса. |
Следует отметить, что в межлопаточных каналах происходит cложное движение жидкости, относительные скорости в радиальных сечениях не одинаковы и параллелограммы скоростей входа и выхода потока отличаются. Учесть все явления происходящие в рабочем колесе, при выводе основного уравнения центробежного насоса не представляется возможным. Поэтому принимают следующие допущения:
Жидкость, перекачиваемая насосом считается идеальной, т.е. совер-шенно несжимаема, и в ней отсутствуют силы вязкости.
Считается, что условное рабочее колесо имеет бесконечно большое число бесконечно тонких лопаток. Тогда можно считать, что между лопатками будут элементарные потоки-струйки, и относительное движение в таких каналах можно характеризовать одним вектором скорости.
В уравнении (1.38) момент количества движении жидкости при входе в колесо относительно оси насоса (рис. 1.22) будет равен
![]() , (1.39)
, (1.39)
где
![]() - вес жидкости.
- вес жидкости.
Момент количества движения на выходе из колеса
![]() (1.40)
(1.40)
Для нахождения момента всех внешних сил , действующих на жидкость в межлопастных каналах относительно оси вращения колеса, необходимо установить эти силы. На жидкость в колесе действуют следующие силы:
Силы тяжести; момент этих сил относительно оси колеса всегда равен нулю, так как рассматриваемый объем представляет собой тело вращения и его центр тяжести находится на оси колеса.
Силы давления на поверхности контрольных сечений; эти силы про-ходят через ось вращения, и, следовательно, их момент так же равен нулю.
Силы трения жидкости на обтекаемых поверхностях; однако эти силы сравнительно невелики и в соответствии с принятыми допущениями их моментом можно пренебречь.
Силы воздействия на протекающую в межлопастных каналах жидкость сил давления со стороны лопастей рабочего колеса; момент этих сил не равен нулю.
Таким
образом, момент всех внешних сил
относительно оси колеса сводится к
моменту динамического воздействия
рабочего колеса
![]() на протекающую через него жидкость,
т.е.
на протекающую через него жидкость,
т.е.
![]() (1.41)
(1.41)
В то же время известно, что мощность, передаваемая жидкости рабочим колесом насоса, равна
![]() , (1.42)
, (1.42)
где
![]() - угловая скорость вращения колеса.
- угловая скорость вращения колеса.
Следовательно
![]() , тогда
, тогда
![]() (1.43)
(1.43)
С
другой стороны, та же мощность
определяется
весом жидкости
и напором
![]() .
.
В
результате получим выражение для
произведения
![]()
![]() (1.44)
(1.44)
где - теоретический напор насоса.
Подставляя в (1.38) выражения (1.39), (1.40) и (1.44) и сокращая , получим
![]() ,
,
или
![]() (1.45)
(1.45)
Так
как
![]() ,
,
![]() ,
окончательно получим
,
окончательно получим
![]() (1.46)
(1.46)
Зависимость (1.46) называется уравнением Эйлера или основным уравнением лопастного насоса.
Основное
уравнение показывает, что теоретический
напор
![]() ,
разви-ваемый насосом, тем больше, чем
больше окружная скорость
,
разви-ваемый насосом, тем больше, чем
больше окружная скорость
![]() на выходе жидкости из рабочего колеса,
т.е. чем больше его диаметр
на выходе жидкости из рабочего колеса,
т.е. чем больше его диаметр
![]() и число обо-ротов
(т.к.
и число обо-ротов
(т.к.
![]() ).
Повышение напора может быть также
достигнуто уменьшением угла
).
Повышение напора может быть также
достигнуто уменьшением угла
![]() Теоретически произведение
Теоретически произведение
![]() имеет максимум при
имеет максимум при
![]() ,
однако практически это означает
прекращение подачи насосом. Поэтому
при конструировании рабочих колес
центробежных насосов обычно принимают
,
однако практически это означает
прекращение подачи насосом. Поэтому
при конструировании рабочих колес
центробежных насосов обычно принимают
![]() .
.
При неизменных параметрах потока на выходе из рабочего колеса напор насоса, согласно основному уравнению, достигает максимума при условии
![]() , (1.47)
, (1.47)
что
практически означает
![]() или
или
![]() .
.
Учитывая, что в рабочее колесо жидкость поступает практически радиально (т.е. ), уравнение (1.46) принимает вид.
![]() (1.48)
(1.48)
Действительный напор, развиваемый насосом, меньше теоретического, так как необходимо учитывать конечное число лопастей в рабочем колесе и расходование напора на преодоление гидравлических сопротивлений.
С учетом этих поправок полный напор центробежного насоса составляет
![]() , (1.49)
, (1.49)
где |
|
- поправочный коэффициент, характеризующий уменьшение напора (за счет уменьшения скорости ) при наличии конечного числа
лопастей рабочего колеса;
|
|
|
-
гидравлический КПД насоса;
|
