Algorithms - R.Sedgewick

For very large graphs, this computation can be organized so that the operations on bits can be done a computer word at a time, which will lead to significant savings in many environments. (As we’ve seen, it is not intended that such optimizations be tried with Pascal.)

Topological Sorting

For many applications involving directed graphs, cyclic graphs do arise. If, however, the graph above modeled a manufacturing line, then it would imply, say, that job A must be done before job G, which must be done before job

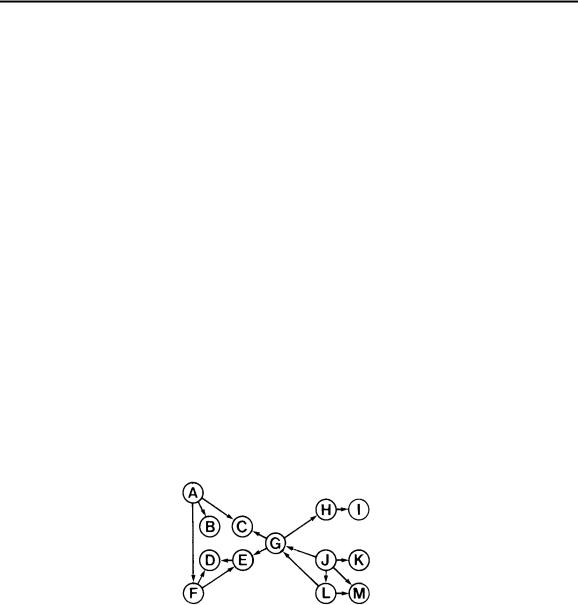
(cycles with all edges pointing the same way) are called for. Such graphs are called directed acyclic graphs, or just dags for short. Dags may have many cycles if the directions on the edges are not taken into account; their defining property is simply that one should never get in a cycle by following edges in the indicated direction. A dag similar to the directed graph above, with a few edges removed or directions switched in order to remove cycles, is given below.

The edge list for this graph is the same as for the connected graph of Chapter 30, but here, again, the order in which the vertices are given when the edge is specified makes a difference.

Dags really are quite different objects from general directed graphs: in a sense, they are part tree, part graph. We can certainly take advantage of their special structure when processing them. Viewed from any vertex, a dag looks like a tree; put another way, the depth-first search forest for a dag has no up edges. For example, the following depth-first search forest describes the operation of dfs on the example dag above.

A fundamental operation on dags is to process the vertices of the graph in such an order that no vertex is processed before any vertex that points to it. For example, the nodes in the above graph could be processed in the following order:

J K L M A G H I F E D B C

If edges were to be drawn with the vertices in these positions, all the edges would go from left to right. As mentioned above, this has obvious application, for example, to graphs which represent manufacturing processes, for it gives a specific way to proceed within the constraints represented by the graph. This operation is called topological sorting, because it involves ordering the vertices of the graph.

In general, the vertex order produced by a topological sort is not unique. For example, the order

A J G F K L E M B H C I D

is a legal topological ordering for our example (and there are many others). In the manufacturing application mentioned, this situation occurs when one job has no direct or indirect dependence on another and thus they can be performed in either order.

It is occasionally useful to interpret the edges in a graph the other way around: to say that an edge directed from x to y means that vertex x “depends” on vertex y. For example, the vertices might represent terms to be defined in a programming language manual (or a book on algorithms!) with an edge from x to y if the definition of x uses y. In this case, it would be useful to find an ordering with the property that every term is defined before

order for our sample graph is:

D E F C B I H G A K M L J

Exercises

1.Give the adjacency matrix for the transitive closure of the example dag given in this chapter.

2.What would be the result of running the transitive closure algorithms on

an undirected graph which is represented with an adjacency matrix?

3.Write a program to determine the number of edges in the transitive closure of a given directed graph, using the adjacency list representation.

4.Discuss how Warshall’s algorithm compares with the transitive closure

6.Does the shortest path algorithm from Chapter 31 work for directed graphs? Explain why or give an example for which it fails.

7.Write a program to determine whether or not a given directed graph is a dag.

8.How many strongly connected components are there in a dag? In a graph with a directed cycle of size V?

9.Use your programs from Chapters 29 and 30 to produce large random directed graphs with V vertices. How many strongly connected com-

ponents do such graphs tend to have?

described by the input edges. (This is not an easy problem: you certainly won’t be able to get as efficient a program as find.)