§3. Суперпозиция полей.
Знание поля точечного заряда позволяет в принципе рассчитывать поля, создаваемые как несколькими зарядами, так и протяженными заряженными телами. Для этого в физике используется простой, но очень важный принцип суперпозиции (наложения) полей, суть которого рассмотрим в данном параграфе.
Пусть имеется
система точечных электрических зарядов
.
Найдём напряженность электрического
поля, создаваемой этими зарядами, в
произвольной точке. Мысленно поместим
в эту точку пробный заряд
.
Опытным путём установлено, что сила
,
с которой система зарядов действует на
этот заряд, равна векторной сумме сил,
приложенных к нему со стороны каждого
из зарядов
:
или в сокращенной записи
.
Разделим это равенство на заряд
или
.
Согласно формуле
(2.1)
- напряжённость электрических полей,
создаваемых отдельными зарядами
в данной точке, а
- напряжённость электрического поля
системы зарядов в той же точке. Поэтому
,
(3.1)
т.е. напряжённость поля системы зарядов равна векторной сумме напряжённостей полей, которые создаёт каждый заряд системы в отдельности. Соотношение (3.1) называют принципом суперпозиции полей.
Пусть поле в точке
А создано
тремя полями, с напряженностями в этой
точке
,
,
(рис. 3.1). Воспользуемся принципом
супепозиции и найдем результирующее
значение напяженности. Для геометрического
сложения используем правилом
многоугольника: последовательно
соединяем, параллельно перенося, все
вектора, так, что к концу предыдущего
вектора присоединяется начало последующего
(рис. 3.2), и вектор соединяющий начало
первого и конец последнего есть резельтат
сложения. В нашем случае
- результирующее значение вектора
напряженности.
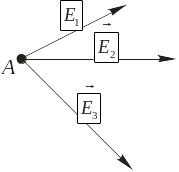
Рис. 3.1 Рис. 3.2
Для нахождения
напряжённости электростатического
поля, создаваемого заряженным протяжённым
телом в некоторой точке, тело мысленно
разбивают на элементарные части с
зарядом
,
которые можно принять за точечные
заряды. Тогда элементарную напряжённость
в этой точке находим по формуле (2.2)
.
Используя принцип суперпозиции полей,
напряжённость поля
в данной точке будет равна:
,
(3.2)
где
— объём тела, поскольку суммирование
элементарных величин означает
интегрирование.
§4. Линии напряжённости.
Очевидно, что напряжённость в каждой точке электрического поля имеет определённую величину и направление. Для наглядного изображения электрического поля пользуются линиями напряжённости или силовыми линиями, т.е. линиями, в каждой точке которых вектор напряжённости электрического поля направлен по касательной к ним (рис. 4.1). Силовые линии проводятся с такой густотой, чтобы число линий, пронизывающих воображаемую площадку в 1 м2, перпендикулярную полю, равнялось величине напряженности поля в данном месте. Тогда по изображению электрического поля можно судить не только о направлении, но и о величине напряженности поля. Например, в окрестностях точки А (рис. 4.1) Е = 2В/м, а в окрестностях точки В Е = 4В/м.
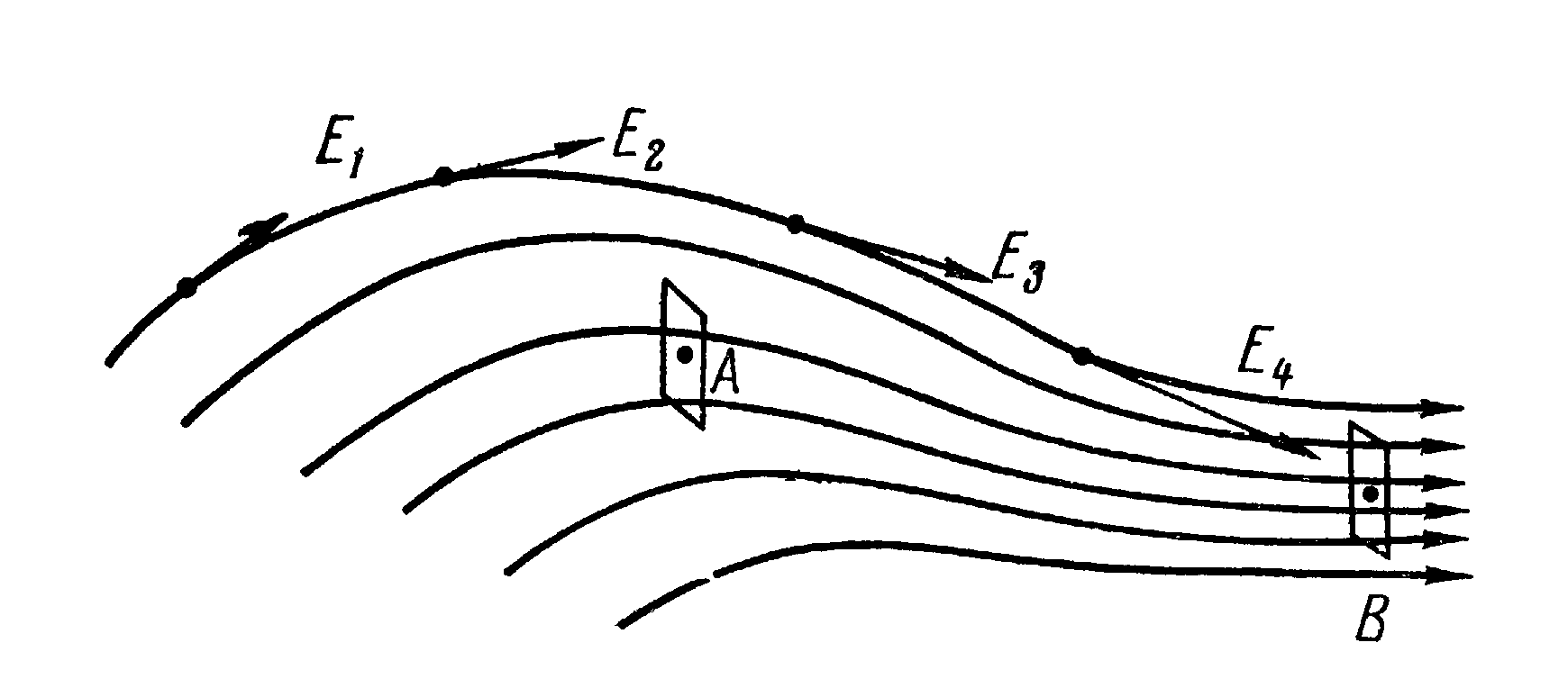
Рис.4.1
Электрическое поле называется однородным, если во всех его точках напряженность одинакова. В противном случае поле называется неоднородным. Графически однородное электрическое поле изображается как параллельные силовые линии, расположенные на одинаковом расстоянии друг от друга. На рис. 4.1 точка В находится в области однородного электрического поля, а точка А в области неоднородного поля.
На рис. 4.2 изображены электрические поля положительного (рис.4.2а) и отрицательного (рис.4.2б) точечных зарядов. Исходя из положительного заряда (или входя в отрицательный заряд) силовые линии теоретически простираются до бесконечности.
а б
Рис.4.2
На рисунке 4.3 с помощью силовых линий изображены электростатические поля для системы двух одноименных (рис.4.3а) и разноименных зарядов (рис.4.3б). Линии напряженности начинаются на положительном заряде и заканчиваются на отрицательном.
А б
Рис.4.3