13.3. Сучасна величина звичайної ренти

Під сучасною, або приведеною, величиною ренти розуміють суму всіх дисконтованих членів ренти на попередній момент. Сучасна величина еквівалентна у фінансовому значенні всім платежам, які охоплюються рентою. Цей показник знаходить широке застосування в розрахунках при погашенні довгострокових позичок, оцінці та порівнянні різного роду зобо­в’язань і надходжень, ефективності інвестицій, розрахунків по страхуванню. Сучасна величина ренти використовується при роз­робці компенсаційних або інших видів довгострокових угод, що передбачають взаємні зобов’язання сторін.

Знайдемо сучасну величину річної ренти, член якої дорівнює R і виплачується в кінці року, ставка відсотків і (відсотки нараховуються в кінці кожного періоду), строк ренти n років. Дисконтована величина першого платежу дорівнює R(1 + i)^–1, другого — R(1 + i)^–2, n-го платежу — R(1 + i)^–n. Цей ряд являє собою геометричну прогресію з першим членом R(1 + i)^–1 і знаменником (1 + i)^–1 з числом членів n. Сучасна величина річної ренти визначається як сума геометричної прогресії за такою формулою:

,

де А — сучасна величина ренти; a_n;i — коефіцієнт приведення ренти. Цей коефіцієнт показує, у скільки разів сучасна величина більша за її член. Графічно сучасну величину ренти можна представити таким чином (рис 13.2):

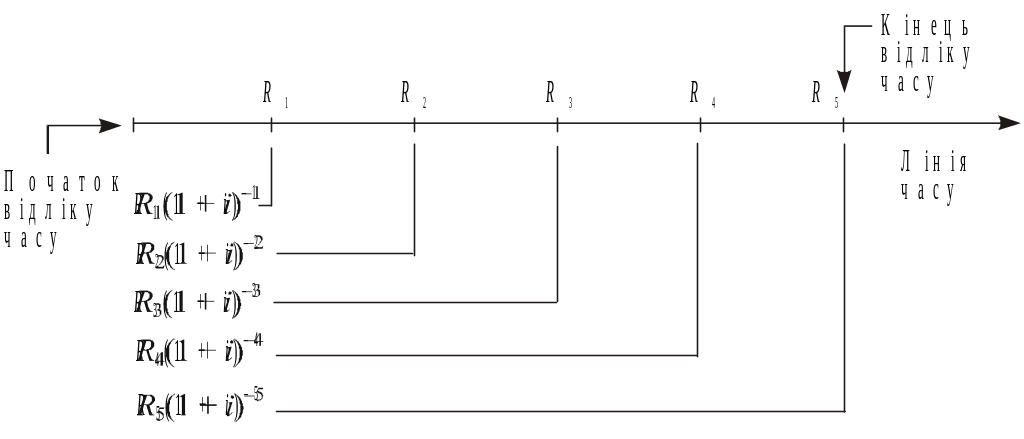
Рис. 13. 2. Розрахунок сучасної величини ренти

Приклад 5. Необхідно визначити суму, яку треба внести на рахунок у банк, який нараховує відсотки в кінці року за ставкою складних відсотків у розмірі 5 % річних, для того щоб виплачувати протягом 5 років наприкінці року додаткову пенсію в сумі 100 грн.

грн.

Річна рента з нарахуванням відсотків m разів на рік.

.

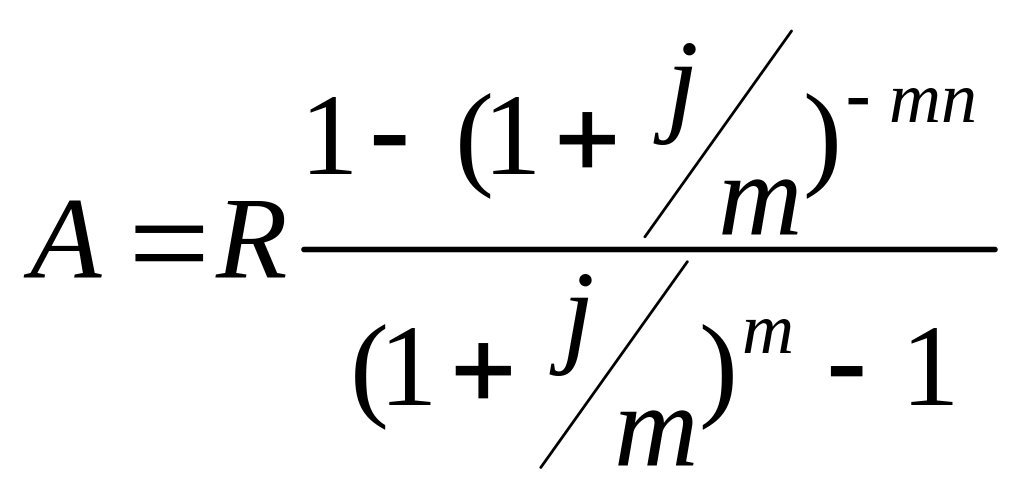Сучасна величина р-термінової ренти (m = 1).

Якщо платежі здійснюються не один, а р разів на рік, а відсотки нараховуються один раз на рік, то коефіцієнт приведення має вигляд:

,

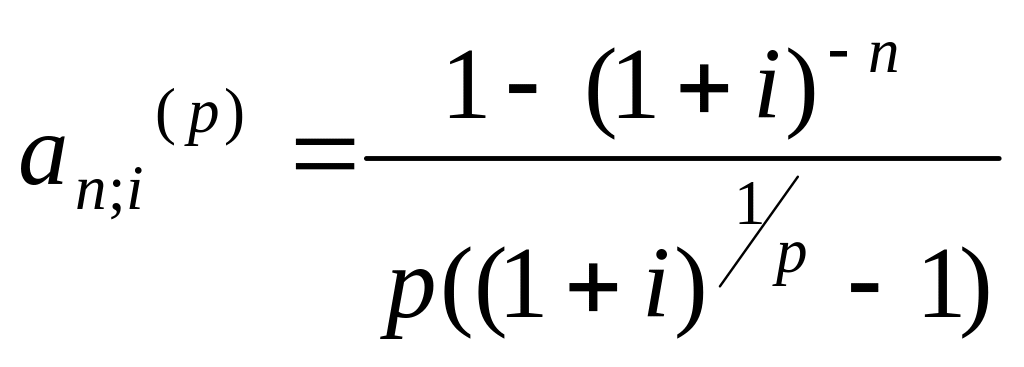а сучасна величина ренти розраховується за формулою:

.

Загальний випадок знаходження сучасної величини ренти, коли відсотки нараховуються m разів, виплати відбуваються р-разів на рік, а :

.

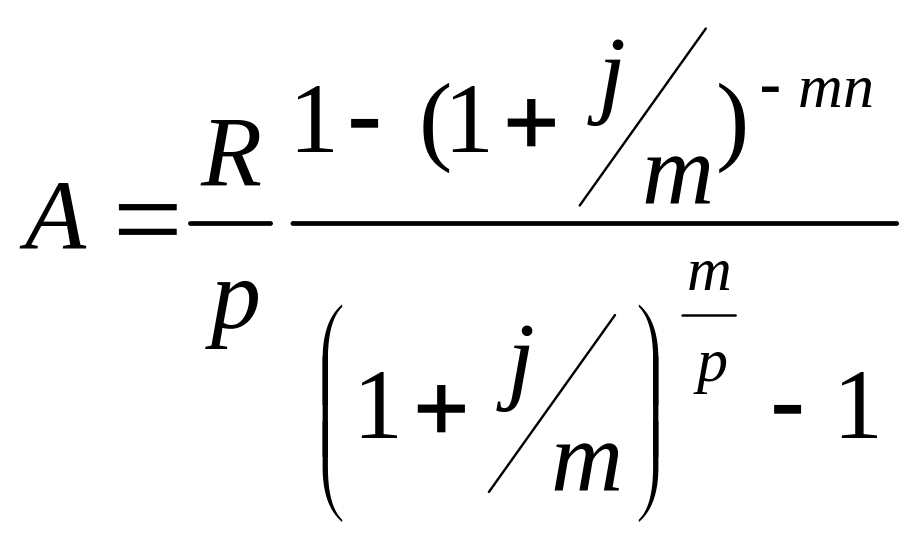Приклад 6. Необхідно визначити суму, потрібну для того, щоб мож­на було виплачувати кредиторові щоквартально 100 грн. протягом 5 ро­ків, якщо на ваш рахунок у банку відсотки нараховуються кожні півроку за складною ставкою відсотків 5 % річних.

Розв’язання: член ренти R = 100 · 4 = 400.

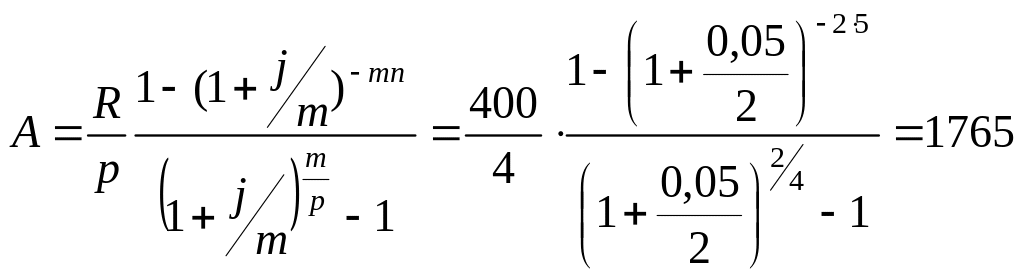грн.

Між нарощеною сумою і сучасною величиною ренти існує взаємозв’язок. Сучасну величину ренти можна отримати шляхом дисконтування нарощеної суми, тобто . Нарощену суму можна також отримати за значенням сучасної величини, тобто S = A(1 + i)ⁿ.

Вічна рента — це послідовність необмеженого числа платежів, які сплачуються протягом нескінченої кількості років. Прикладом такої ренти є виплата дивідендів за акціями, окремі види платежів, внески до Пенсійного фонду.

Коефіцієнт приведення вічної ренти:

.

Формула сучасної величини вічної ренти має такий вигляд:

.

Приклад 7. Скільки коштує акція з щорічними дивідендами 40 грн., якщо відсоткова ставка, за якою дисконтуються подібні акції, дорівнює 8 %?

Розв’язання:

грн., тобто вартість даної акції 500 грн.