
МАТЕМАТИКА (I курс)
Профиль «Информатика и информационные технологии в образовании»
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
ЗАДАНИЕ №1 (МНОЖЕСТВА)
Вычислить
![]() для множеств А
и В:
для множеств А
и В:
ВАРИАНТ № |
ЗАДАННЫЕ МНОЖЕСТВА |
1 |
(1)A={3;4;},B=[5;8),
(2)
A=[-3;2), В=[0; (3) A=[-1;1), B=[2;4) |
2 |
(1)A=[-2;3), B={4;0}, (2) A=(- ;3), B=[0;6), (3)A=[-3;2), B=[0; ) |
3 |
1)A=(- ;2), B=[0;3), (2)A=[-2;4), B=(0;5) (3)A={3;5;}, B=[-1;3) |
4 |
(1)A=[-2;5), B=(0;7), (2) A=[-1; ), B=[1;4), (3) A=[-2;3], B={0;2} |
5 |
(1)A={2;4}, B=[1;3], (2) A=(-1;7], B=(-3;0], (3) A=[-1; ), B=[1;6). |
6 |
(1)A=[3;5),B=[-2;4), (2) A=[-3;5), B=(-2; ), (3)A=[-3;3), B={1;2} |
7 |
(1)A=[-1; ), B=[2;4), (2) A=[-2;4), B=(0;5), (3) A=[-2; ), B={0;2} |
8 |
(1)A=[-2;4), B=(0;5), (2) A=[-3;5), B=(-2; ), (3)A=[-2;1), B={1;2} |
9 |
(1)A={2;4}, B=[1;3], (2) A=(-1;7], B=(-3;0], (3) A=[-1; ), B=[1;6). |
10 |
(1)
A=[-1; (3) A=[-2; ), B={0;2} |
11 |
(1)A={3;4;},B=[5;8), (2) A=[-3;2), В=[0; ), (3) A=[-1;1), B=[2;4). |
12 |
(1)A=[-2;5), B=(0;7),(2) A=[-1; ), B=[1;4), (3) A=[-2;3], B={0;2}. |
13 |
(1)A=(- ;2), B=[0;3), (2)A=[-2;4), B=(0;5) (3)A={3;5;}, B=[-1;3). |
14 |
(1)A=[-2;3), B={4;0}, (2) A=(- ;3), B=[0;6), (3)A=[-3;2), B=[0; ). |
15 |
(1)A=[-2;4), B=(0;5),(2) A=[-3;5), B=(-2; ), (3)A=[-2;1), B={1;2}. |
16 |
(1)A=[3;5),B=[-2;4),(2) A=[-3;5), B=(-2; ), (3)A=[-3;3), B={1;2}. |
17 |
(1)A={3;4;},B=[5;8), (2) A=[-3;2), В=[0; ), (3) A=[-1;1), B=[2;4). |
18 |
(1)A=[-2;3), B={4;0}, (2) A=(- ;3), B=[0;6), (3)A=[-3;2), B=[0; ). |
19 |
(1)A=(- ;2), B=[0;3), (2)A=[-2;4), B=(0;5) (3)A={3;5;}, B=[-1;3). |
20 |
(1)A=[-2;5), B=(0;7),(2) A=[-1; ), B=[1;4), (3) A=[-2;3], B={0;2}. |
21 |
(1)A={2;4}, B=[1;3], (2) A=(-1;7], B=(-3;0], (3) A=[-1; ), B=[1;6). |
22 |
(1)A=[3;5),B=[-2;4),(2) A=[-3;5), B=(-2; ), (3)A=[-3;3), B={1;2}. |
23 |
(1) A=[-1; ); B=[2;4); (2) A=[-2;4); B=(0;5) (3) A=[-2; ), B={0;2} |
24 |
(1)A=[3;5),B=[-2;4),(2) A=[-3;5), B=(-2; ), (3)A=[-3;3), B={1;2}. |
25 |
(1)A={2;4}, B=[1;3], (2) A=(-1;7], B=(-3;0], (3) A=[-1; ), B=[1;6). |
Задание №2 (определители)
Вычислить определители третьего порядка, используя метод разложения определителя по элементам строки (столбца):
ВАРИАНТ № |
Заданные определители |
1 |
А= |
2 |
А= |
3 |
А= |
4 |
А= |
5 |
А= |
6 |
А= |
7 |
А= |
8 |
А= |
9 |
А= , В= , С= , D= |
10 |
А= , В= , С= , D= |
11 |
А= , В= , С= , D= |
12 |
А= , В= , С= , D= |
13 |
А= |
14 |
А= , В= , С= , D= |
15 |
А= , В= , С= , D= |
16 |
А= , В= , С= , D= |
17 |
А= , В= , С= , D= |
18 |
А= , В= , С= , D= |
19 |
А= , В= , С= , D= |
20 |
А= , В= , С= , D= |
21 |
А= , В= , С= , D= |
22 |
A= , В= , С= , D= |
23 |
А= , В= , С= , D= |
24 |
А= , В= , С= , D= |
25 |
А= , В= , С= , D= |
Задание №3 (векторы)
Заданы три точки А, В, С своими координатами. Найти скалярное, векторное, смешанное произведение векторов, модуль заданного вектора.
ВАРИАНТ № |
Заданные точки А, В, С |
Найти
|
Найти
|
Найти
|
1 |
A(2;3;1),B(1;4;0), C(2;-1;-2) |
|
|
|
2 |
A(3;-2;3),B(-1;3;-2) C(0;2;-1) |
|
|
|
3 |
A(-2;0;1),B(3;-1;2), C(2;1;-3) |
|
|
|
4 |
A(3;-2;1),B(4;2;-3), C(0;1;-1) |
|
|
|
5 |
A(4;-3;2),B(2;1;-4), C(0;-1;3) |
|
|
|
6 |
A(5;2;4),B(-2;3;-1), C(-2;-4;1) |
|
|
|
7 |
A(-1;2;-3), B(0;-2;5), C(-2;3;-1) |
|
|
|
8 |
A(-1;2;4),B(3;2;-2), C(0;2;-1) |
|
|
|
9 |
A(3;-2;3),B(-1;3;-2) C(0;2;-1) |
|
|
|
10 |
A(4;-3;2),B(2;1;-4), C(0;-1;3) |
|
|
|
11 |
A(-2;0;1),B(3;-1;2), C(2;1;-3) |
|
|
|
12 |
A(2;3;1),B(1;4;0), C(2;-1;-2) |
|
|
|
13 |
A(3;-2;1),B(4;2;-3), C(0;1;-1) |
|
|
|
14 |
A(-1;2;4),B(3;2;-2), C(0;2;-1) |
|
|
|
15 |
A(-1;2;-3), B(0;-2;5) C(-2;3;-1) |
|
|
|
16 |
A(5;2;4),B(-2;3;-1), C(-2;-4;1) |
|
|
|
17 |
A(2;3;1),B(1;4;0), C(2;-1;-2) |
|
|
|
18 |
A(3;-2;3),B(-1;3;-2) C(0;2;-1) |
|
|
|
19 |
A(-2;0;1),B(3;-1;2), C(2;1;-3) |
|
|
|
20 |
A(3;-2;1),B(4;2;-3), C(0;1;-1) |
|
|
|
21 |
A(4;-3;2),B(2;1;-4), C(0;-1;3) |
|
|
|
22 |
A(5;2;4),B(-2;3;-1), C(-2;-4;1) |
|
|
|
23 |
A(-1;2;-3),B(0;-2;5) C(-2;3;-1) |
|
|
|
24 |
A(-1;2;4),B(3;2;-2), C(0;2;-1) |
|
|
|
25 |
A(3;-2;3),B(-1;3;-2) C(0;2;-1) |
|
|
|

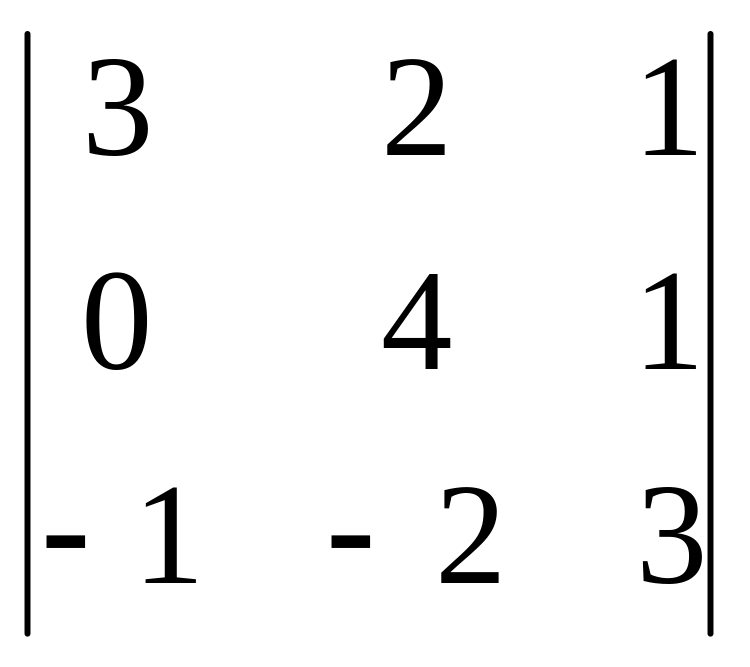 ,
В=
,
В=
 ,
С=
,
С=
 ,
D=
,
D=
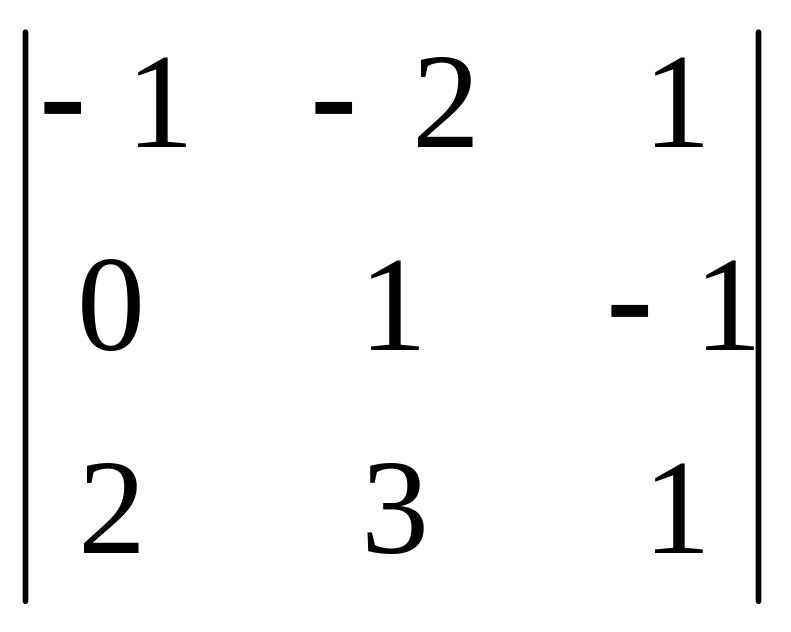
 ,
В=
,
В=
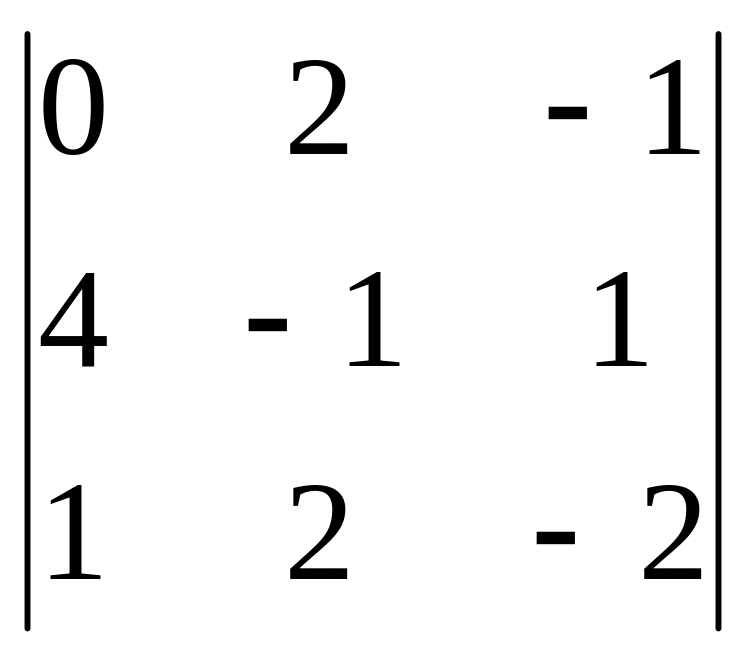 ,
С=
,
С=
 ,
D=
,
D=

 ,
В=
,
В=
 ,
С=
,
С=
 ,
D=
,
D=
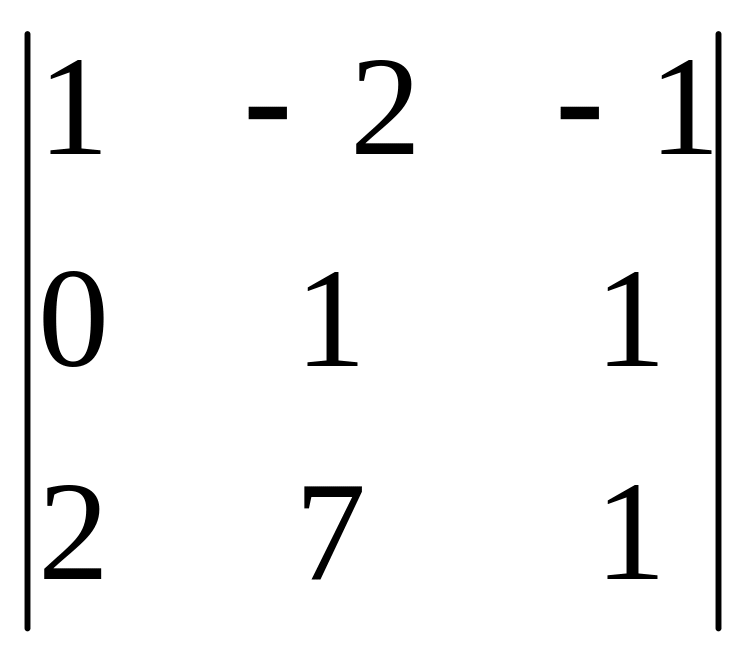
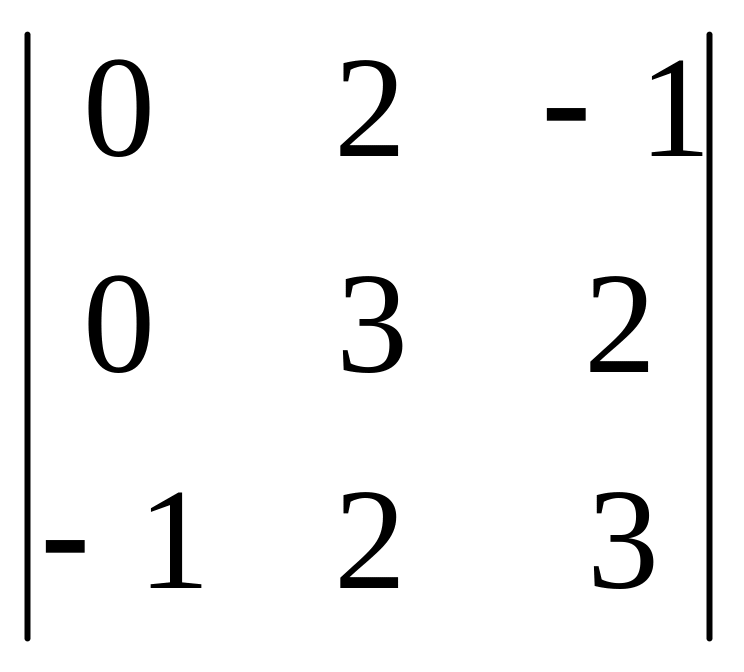 ,
В=
,
В=
 ,
С=
,
С=
 ,
D=
,
D=

 ,
В=
,
В=
 ,
С=
,
С=
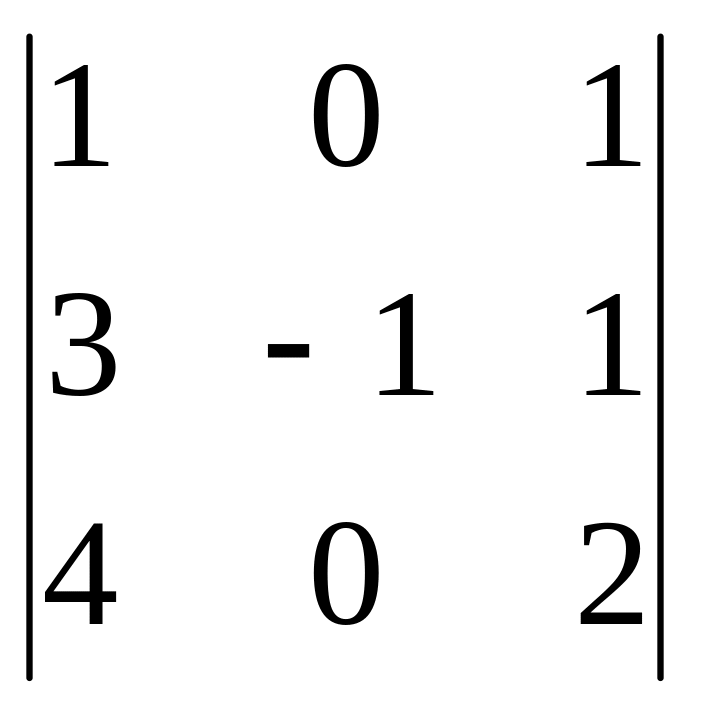 ,
D=
,
D=
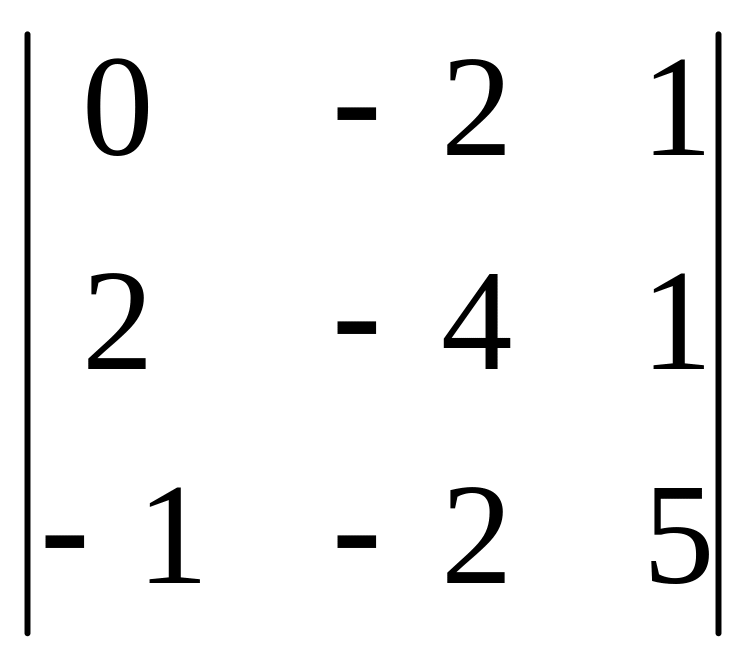 ,
В=
,
В=
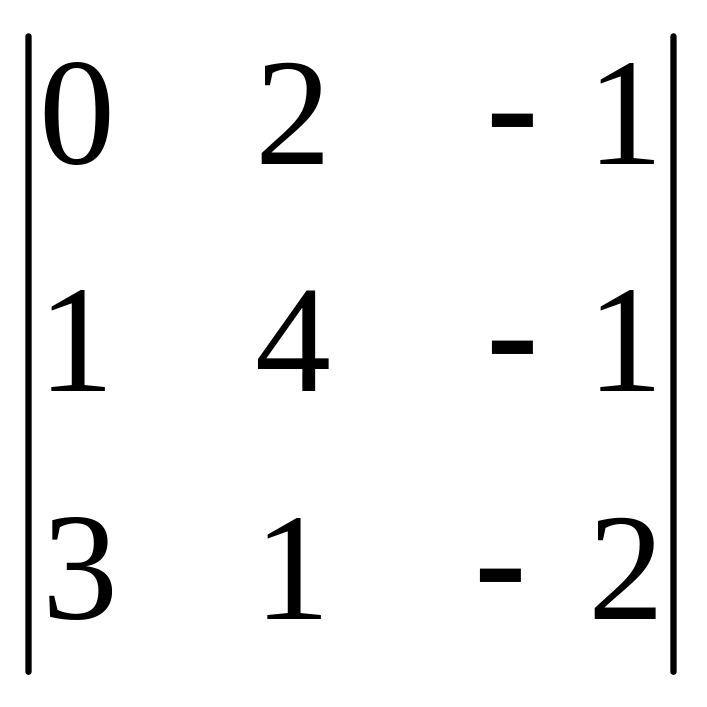 ,
С=
,
С=
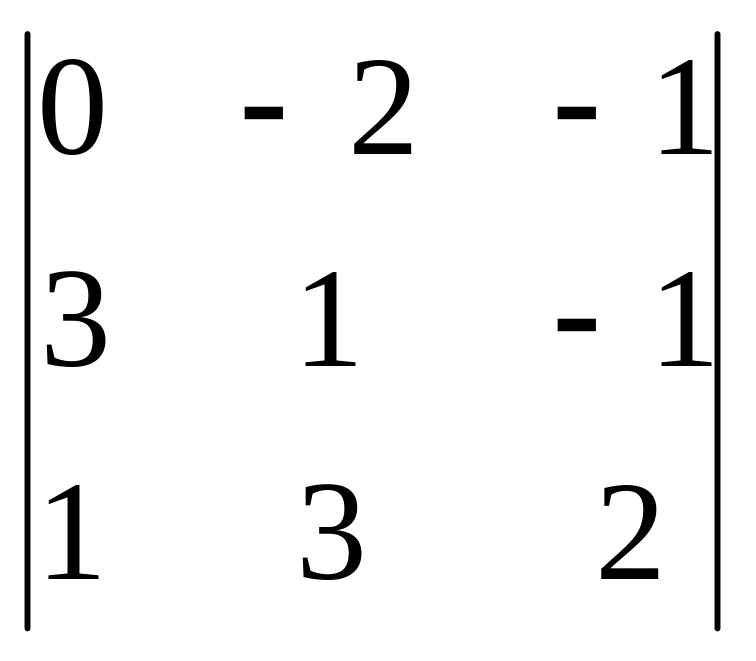 ,
D=
,
D=
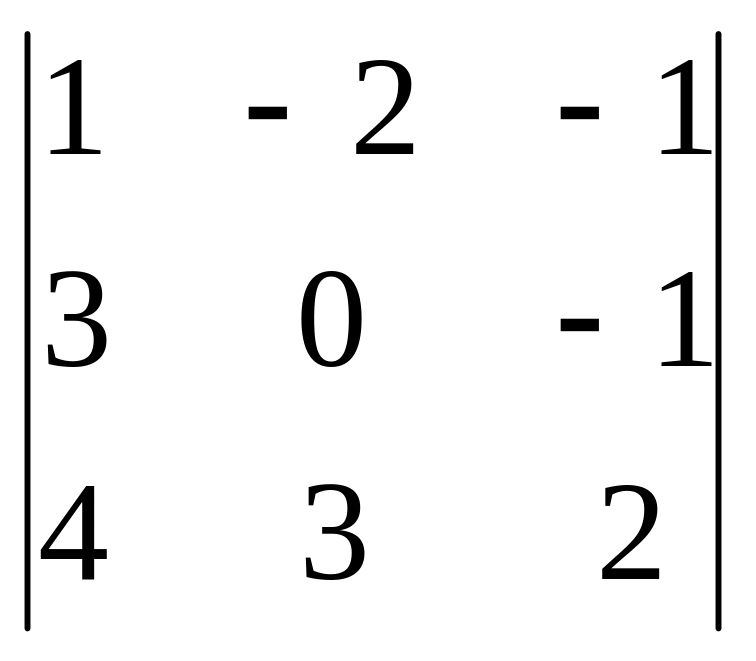
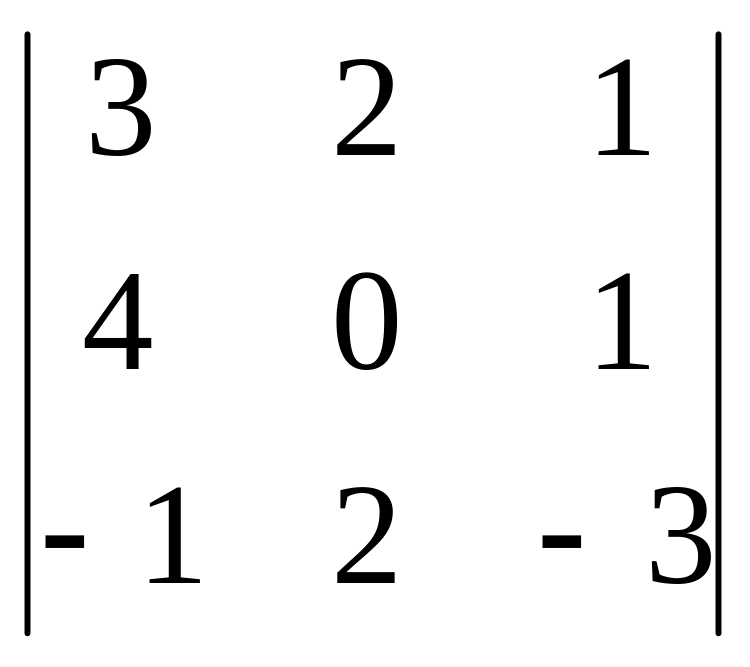 ,
В=
,
В=
 ,
С=
,
С=
 ,
D=
,
D=

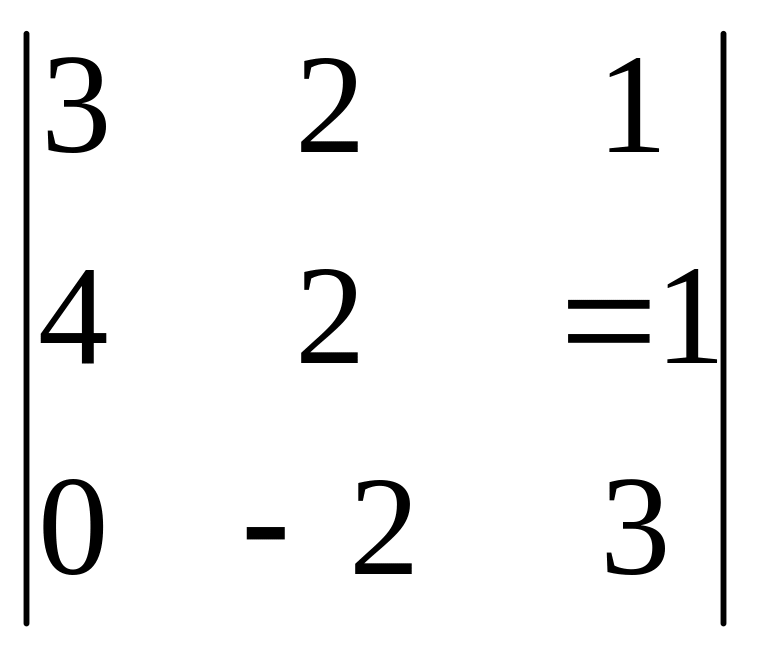 ,
В=
,
В=
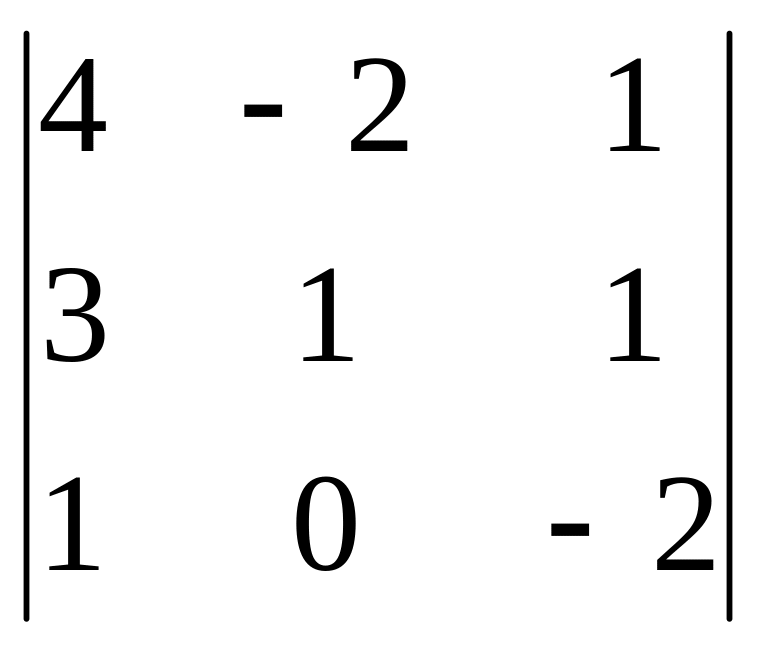 ,
С=
,
С=
 ,
D=
,
D=

 ,
В=
,
В=
 ,
С=
,
С=
 ,
D=
,
D=
