Тема XIII - числовые ряды . План лекции (1 час)
1. Понятие числового ряда.
2. Сходимость числового ряда.
3. Признаки сходимости рядов.
4. Положительные ряды, их сходимость.
5. Признаки сходимости положительных рядов: признак сравнения, признак Даламбера.
6. Знакочередующиеся ряды.
7. Абсолютная и условная сходимость числового ряда.
Конспект лекции
1.Для
бесконечной последовательности
составим сумму вида
(1)
– это числовой ряд,
- члены ряда. Для ряда (1) составляются
частичные
суммы:
,
частичные суммы ряда – это конечные
суммы (часто называются отрезками).
2.Составим
последовательность частичных сумм:
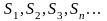(2).
Ряд называется сходящимся, если существует
предел
,
число S
– это сумма ряда (1):
(3)
(если S
существует, то ряд сходится). Ряд (1)
расходящийся, если предела
не существует. Например, ряд
(при
|q|<1
- бесконечно убывающая геометрическая
прогрессия,
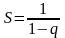- сумма прогрессии),
(4)- ряд сходится при |q|<1.
Если q=1,
то
и
-
ряд (4) расходится.
3.
Из ряда (1)
выделим первые n
членов:
,
оставшийся ряд
(5)
– m
– ый остаток
ряда (1).
Тогда ряд (5) сходится или расходится
одновременно с рядом (1). Поэтому при
исследовании ряда (1) можно рассматривать
только остаток ряда. сли ряд (1) сходится,
тогда сходится и остаток ряда – ряд
(5). Пусть
-
сумма ряда (1);
-
сумма первых m
членов ряда (1);
- сумма остатка ряда (1), тогда
,
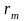- это та погрешность, которая допускается,
если вместо суммы S
сходящегося ряда (1) рассматриваем сумму
его первых членов: чем больше m,
тем меньше эта погрешность:
,
(предел суммы
m-го
остатка равен нулю). Если ряд (1) сходится,
то
(чем
больше m,
тем меньше члены ряда). Необходимый
признак сходимости
ряда:
если ряд (1) сходится, то общий член ряда
(1) стремится к нулю при неограниченном
возрастании числа членов ряда: для
сходящегося ряда
Следствие:
если общий член ряда (1) при
не стремится к нулю, то ряд (1) расходится.
Свойства
сходящихся рядов:
[1]. Если ряд (1) сходится и его сумма равна
S,
то ряд
(6)
тоже сходится, его сумма равна CS
, где С
– постоянная.[2]. Для двух сходящихся
рядов
с суммой S
(1) и
(7)
c
суммой
ряд
тоже сходится с суммой
4.Положительный
ряд – это ряд с неотрицательными членами,
(1) – ряд положительный при
.
Если
,
тогда
- последовательность
-
неубывающая. Из теории пределов: если
последовательность неубывающая, то она
ограничена сверху. Поэтому, чтобы
положительный ряд сходился, необходимо
и достаточно, чтобы последовательность
частичных сумм
была ограничена сверху.
5.Два
основных признака сходимости положительных
рядов: (I).
Признак
сравнения:
если
- два положительных ряда и
,
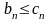то (а) из сходимости ряда (С)
следует сходимость ряда (В);
(b)
из расходимости ряда (В)
следует расходимость ряда (С).
Например, для ряда
(с)
сравним его члены с членами специально
подобранного ряда
:
(d)
(условие (b)
можно проверить непосредственной
подстановкой). Члены ряда (d)
представим в виде:
. Частичная сумма ряда (d)
:
,
тогда
- ряд (d)
сходится. Из
по первому признаку сравнения – ряд
(c)
тоже сходится.
(II).
Признак сходимости Даламбера
(1717
– 1783гг.). Если ряд (1) положительный и
существует предел
,
то (а) при
- ряд сходится; (b)
при
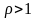- ряд расходится. При
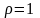признак Даламбера ответа не дает.
Например, для ряда
:
.
По признаку Даламбера:
-
ряд сходится.
6.Ряд
вида
(8)
- знакочередующийся. По теореме
Лейбница: если в ряду (8)
(члены ряда по абсолютной величине
убывают) и
,
то ряд (8) сходится. Например, для ряда
ряд сходится, так как
7.Кроме
рядов положительных и знакочередующихся
есть ряды с произвольно расположенными
знаками у членов. Если
(1)
- ряд с любыми знаками членов, а ряд
(9)
составлен из модулей членов ряда (1), то
если сходится ряд (9), то сходится и ряд
(1). Ряд (1) –ряд абсолютно сходящийся,
если сходится ряд (9). Если ряд (1) сходится,
а ряд (9) расходится, то ряд (1) - условно
сходящийся.