3.12 Системы с хаотическими колебаниями

Новая парадигма динамики

Томас Кун в книге «Структура научных революций» утверждает, что крупные изменения происходят в науке в общем не тогда, когда выдвигаются новые теории, а когда меняются простые модели, с помощью которых ученые формулируют и осваивают теорию. Концептуальная модель или задача, которая охватывает основные свойства целого класса задач, названа им «парадигмой». Модель, состоящая из массы и пружины, является такой парадигмой теории колебаний. В области нелинейной динамики классическими парадигмами стали движение маятника и задача трех тел небесной механики.

Нет лучшего примера теории, новые модели и парадигмы которой обещают значительные перемены в естественнонаучном и математическом мышлении, чем нелинейная динамика, испытывающая сейчас революционные изменения. Двумя главными парадигмами здесь являются аттрактор Лоренца и логистическое уравнение. Эти два примера заключают в себе многие особенности хаотической динамики, такие, как разбегающиеся траектории, субгармонические бифуркации, удвоение периода, отображения Пуанкаре и фрактальные размерности. Как для освоения теории линейных колебаний необходимо изучить все тонкости модели из массы с пружиной, без которых нельзя понять колебания сложных систем. Каждому, кто ищет свой путь в современной нелинейной динамике, не обойтись без понимания явлений, скрытых в модели Лоренца и логистическом уравнении. Другие, менее яркие парадигмы также важны для понимания и развития теории динамических систем. Среди них вынужденные движения осциллятора Ван дер Поля, модели осциллятора Дуффинга, разработанные Уэдой и Холмсом.

Математические модели хаотических физических систем. Мы будем отличать математические модели, построенные для физических процессов с хаотической динамикой, и физические эксперименты, в которых непосредственно наблюдаются хаотические движения. Читатели, имеющие в распоряжении небольшой компьютер, могут наблюдать хаотические решения для многих из этих моделей с помощью численного интегрирования методом Рунге-Кутта.

Тепловая конвекция в жидкости. По-видимому, самой знаменитой сейчас моделью является система Лоренца, которая возникла в результате попытки моделирования динамики атмосферы. Представим себе слой жидкости, находящийся под действием силы тяготения, который подогревается снизу, так что поперек слоя поддерживается разность температур (см. рисунок). Когда эта разность становится достаточно большой, возникают циркуляционные, подобные вихрям, движения жидкости, в которых теплый воздух (жидкость) поднимается, а холодный – опускается. Верхушки параллельных рядов конвективных валов можно иногда увидеть, пролетая над слоем облаков. Двумерное конвективное течение можно описать с помощью классического уравнения Навье-Стокса. Это уравнение раскладывается по фурье-гармоникам вдоль двух пространственных направлений, а на поверхности и на дне слоя жидкости задаются граничные условия. При малых разностях температур жидкость неподвижна, но при некотором критическом значении возникает конвективное, т.е. циркуляционное течение. Это движение называют конвекцией Рзле-Бенара.

Рисунок 1.71 - Тепловая конвекция а – схематическое изображение конвективных валов в подогреваемой снизу жидкости; б – три неустойчивые сингулярные точки в фазовом пространстве уравнений Лоренца

Лоренц изучал разложения Фурье, в которых оставлено всего три гармоники. При принятых упрощениях скорость жидкости следующим образом выражается через функцию тока :

.

В модели Лоренца безразмерные функции тока и возмущенная температура записываются в виде

,

где толщина слоя жидкости принята равной единице. В результате получаются следующие уравнения для :

,

Параметр – безразмерное отношение коэффициентов вязкости и теплопроводности (число Прандтля), – безразмерный градиент температуры (связанный с числом Рэлея), a – геометрический множитель, причем (рисунок 1.72)

Рисунок 1.72 - Траектория, отвечающая хаотическому решению уравнений Лоренца для тепловой конвекции жидкости, по результатам численного моделирования

При наборе параметров 10, 28 и 8/3 (использованном Лоренцем) имеются три точки равновесия, и все они неустойчивы. В начале координат расположена седловая точка, а две другие – неустойчивые фокусы, т.е. спиральные точки равновесия. Тем не менее, можно показать, что движение глобально ограничено. Поэтому траекториям не остается ничего другого, кроме как оставаться внутри эллипсоидальной области в фазовом пространстве. Пример таких блуждающих траекторий, полученный при численных расчетах, показан на рисунке.

Траектория, отвечающая хаотическому решению уравнений Лоренца для конвекции жидкости, по результатам численного моделирования.

Часто случается, что важные открытия делаются не одним исследователем – несколько человек в разных местах примерно одновременно обнаруживают новое явление. Так случилось и с моделями динамики тепловой конвекции, имеющими небольшое число степеней свободы. Выше мы обсудили ныне знаменитые уравнения Лоренца, которые через некоторое время после их получения вызвали громадный интерес математиков. Но примерно в то же время Мур и Шпигель, сотрудники соответственно Института им. Годдарда и Нью-йоркского университета, предложили модель неустойчивых колебаний жидкости, которая вращается, содержит магнитное поле или является сжимаемой и в которой присутствует тепловая диссипация. Как и уравнения Лоренца, полученные в их статье уравнения эквивалентны трем дифференциальным уравнениям первого порядка.

Пусть через обозначено вертикальное смещение массы сжимаемой жидкости в горизонтально стратифицированной среде. Силами, восстанавливающими исходное состояние, являются упругость пружины и сила плавучести, которая возникает благодаря тяготению. Кроме того, жидкий элемент может обмениваться теплом с окружающей средой.

Динамика модели описывается связанными уравнением второго порядка (закон Ньютона) и уравнением переноса тепла, имеющим первый порядок. В результате возникает уравнение третьего порядка. В безразмерном виде оно записывается как

,

где использовано предположение о нелинейном профиле температуры вида

.

Уравнение можно привести к виду

В уравнении и – безразмерные комплексы, имеющие следующий физический смысл:

,

При численном исследовании этого уравнения обнаружили целую область апериодического движения, показанную на рисунке. Исследовали устойчивость периодических решений в апериодическом режиме (рисунок 1.73).

Рисунок 1.73 - Система из пружины и массы (аналог модели тепловой конвекции); б – область непериодических движений в пространстве безразмерных параметров модели тепловой конвекции

Предел соответствует случаю нулевой диссипации. Как показали Бейкер и др., в этом предельном случае больших периодические решения в области периодических движений становятся локально неустойчивыми. Это сочетание глобальной устойчивости и локальной неустойчивости, по-видимому, характерно для хаотических дифференциальных уравнений. В более поздней работе изучен более общий класс уравнений третьего порядка вида

где имеет смысл потенциальной энергии.

Приведенная система уравнений описывает также осциллятор второго порядка с управляющей обратной связью (параметр ).

Историков науки ждет интересная задача понять, почему системе Лоренца посвящено так много исследований, а модель Мура – Шпигеля практически игнорируется математиками. В обеих работах моделируется конвекция. Лоренц опубликовал свою статью в Journal of Atmospheric Sciences, а Мур и Шпигель – в Astrophysical Journal.

Задача с соударениями

Задачи с соударениями приводят непосредственно к разностным уравнениям или отображениям, которые при определенном выборе параметров часто обнаруживают хаотические колебания. Классическое отображение такого типа описывает движение частицы между двумя стенками. Если одна из стенок неподвижна, а другая колеблется (рисунок 1.74), то задача называется моделью Ферми ускорения космических лучей и описывает поведение заряженных частиц в движущихся магнитных полях. Эта модель очень подробно обсуждается Лихтенбергом и Либерманом [110] в их доступно написанной монографии о стохастическом движении. Исследовано несколько систем разностных уравнений, описывающих эту модель. Одна из таких систем, в которой колеблющаяся стенка передает импульс, не меняя положение частицы, имеет вид

,

где – скорость после соударения, – момент соударения, – импульс на единицу массы, который может передать стенка, а – расстояние между стенками.

Численные исследования этой и аналогичных задач обнаруживают существование решений стохастического типа, в которых тысячи итераций отображения заполняют области фазового пространства ,

Рисунок 1.74 - Модель динамики частицы, отскакивающей от периодически колеблющейся стенки

Модель одного из механических устройств с зазором показанна на следующем рисунке 1.75. Некоторая масса свободно скользит с трением вдоль оси, пока не наталкивается на жесткие пружины, расположенные по обе стороны).

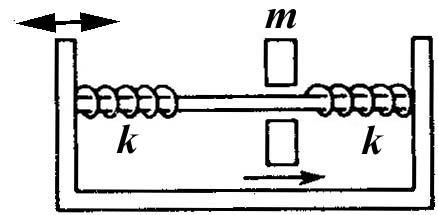
Рисунок 1.75 - Модель эксперимента с колебаниями массы с фазами отключения восстанавливающей силы

Более близкий физический смысл имеет другая математическая модель, в которой шарик подскакивает на колеблющейся поверхности. Сделав некоторое предположение о потерях энергии при каждом соударении, можно получить следующие разностные уравнения:

Здесь – безразмерный момент времени соударения, a – скорость после него.

Как явствует из рисунка, стационарное синусоидальное движение стола может привести к непериодическому движению шарика.

Исследования хаотических движений в консервативных (без затухания) системах имеют более давнюю историю, чем привлекающие ныне всеобщий интерес исследования хаотических режимов в диссипативных системах. Но поскольку практическое приложение консервативных динамических систем ограничено такими областями, как небесная механика, физика плазмы и физика ускорителей, инженеры берут на вооружение успехи, достигнутые в динамике консервативных систем, не с такой готовностью, как успехи, достигнутые в других областях нелинейной динамики (рисунок 1.76).

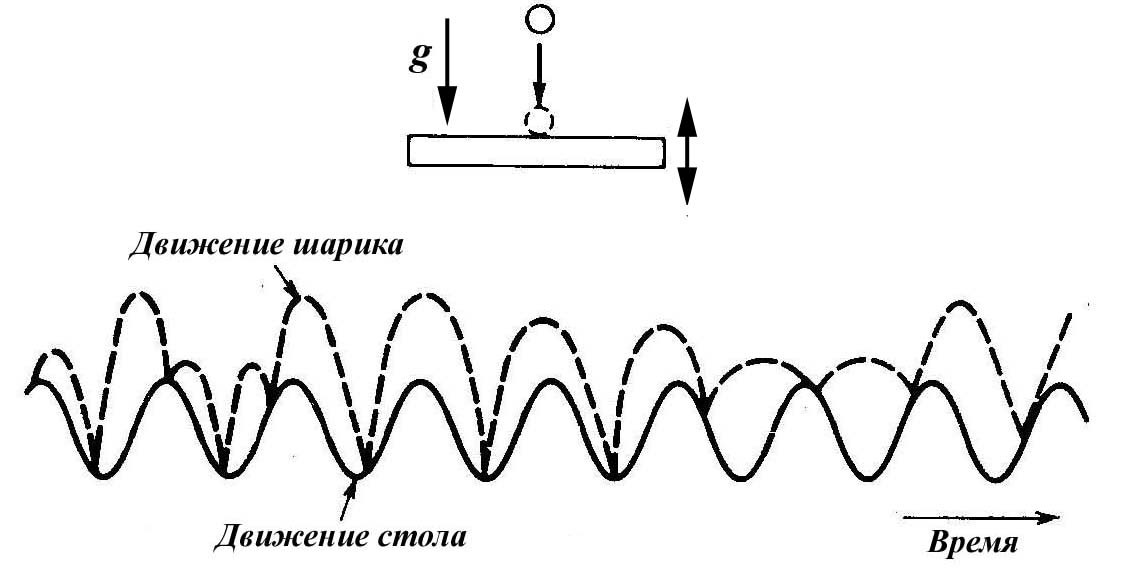
Рисунок 1.76 - Хаотическая эволюция движения шарика, подскакивающего на периодически колеблющемся столе

Задача с потенциалом в виде двойной ямы

Модель вынужденных колебаний изогнутого стержня была построена Холмсом на основе уравнения типа Дуффинга. С помощью аналогового моделирования им доказана возможность хаотических колебаний этой системы. В безразмерном виде полученное, Холмсом уравнение таково:

,

где – поперечное смещение стержня, который описывается простой одномодовой моделью.

Это уравнение может также служить моделью частицы в потенциале из двух ям. Эта модель использовалась и при исследовании плазменных колебаний. На рисунке показано отображение Пуанкаре соответствующего странного аттрактора.

К этим примерам близка задача о провале арки с шарниром, вызванном колебаниями (рисунок 1.77).

Рисунок 1.77 - Схема арки с шарниром. Вынужденные колебания, сопровождающиеся провалами арки, могут происходить в хаотическом режиме

Это явление описывается уравнением

.

Если сохранить только кубичные нелинейности, то это уравнение принимает вид, характерный для осциллятора Дуффинга с двумя потенциальными ямами.

Хаотические колебания маятника

Движение частицы в силовых полях, которые периодичны как в пространстве, так и во времени, служит моделью ряда процессов в Физических системах. Среди них классический маятник, заряженная частица в движущемся электрическом поле, синхронные роторы и переход Джозефсона. Например, нелинейная динамика частицы движущейся в бегущем электрическом поле, описывается уравнением

,

где – периодическая функция. Изучение вынужденных колебаний маятника, описываемых уравнением

также выявило сложные динамические процессы и хаотические колебания.

Параметрическими колебаниями называют колебания системы при периодических изменениях во времени одного из нескольких параметров системы. Например, стержень на простой подвеске, на который действует осевое доизгибное сжатие, в одномодовом приближении описывается уравнением

.

Это линейное дифференциальное уравнение в обыкновенных производных является хорошо известным уравнением Матье. При определенных значениях и это уравнение имеет неустойчивые колебательные решения. Влияние нелинейностей превращает эти колебания в предельный цикл.

Аналогичный пример – маятник с колеблющейся точкой подвеса. Математическое описание такого маятника приводит к уравнению

.

этих численных решениях наблюдаются удвоения периода, и для шестой субгармонической бифуркации оценка числа Фейгенбаума дала .

Рисунок 1.78 - Маятник с параметрическим возбуждением

Сферический маятник

Были проанализированы сложные динамические процессы в сферическом маятнике с двумя степенями свободы. В численных экспериментах им найдены хаотические решения этой задачи, возникающие, когда точка подвеса совершает вынужденные периодические движения. Уравнения движения можно получить из лагранжиана, имеющего вид

,

где – длина маятника, а координаты подчиняются связи

.

Координата точки подвеса есть , а тяготение действует вдоль оси .

Используя методы теории возмущений, и т полученные уравнения движения преобразуется с помощью соотношений

где и . В результате получается следующая система четырех уравнений первого порядка для , в которую добавлено слабое затухание (описываемое коэффициентом ):

где и зависят от переменных . Точки равновесия системы уравнений соответствуют периодическим плоским либо пространственным движениям. Численное решение этой системы уравнений обнаруживает переход от замкнутых орбит и дискретных спектров к сложным орбитам и широким спектрам, характерным для хаотического движения.

Подталкиваемый ротор

Большинство дифференциальных уравнений, моделирующих физические системы, нельзя решить аналитически. Исключением из этого правила является класс задач с импульсными силами, крутящими моментами или напряжениями. В обсуждаемом здесь примере рассматривается ротатор с моментом инерции и затуханием , на который действует как постоянный крутящий момент , так и периодическая серия импульсных толчков.

Уравнение движения, описывающее изменение углового момента ротатора

, где .

Выражение обозначает дельта-функцию, которая равна нулю повсюду, кроме значений , и площадь под которой равна единице. В промежутки времени , где , изменение углового момента описывается соотношением

.

Если ротатор подталкивается вертикальной силой, то импульсный крутящий момент пропорционален . При уравнение имеет стационарное решение , . Чтобы получить отображение Пуанкаре, выберем сечение непосредственно перед каждым импульсом. Итак, определим , . Чтобы связать с , необходимо решить линейное дифференциальное уравнение для периода между импульсами и использовать условие скачка углового момента в момент импульса. Между импульсами скорость вращения ведет себя следующим образом (рисунок 1.79):

.

Рисунок 1.79 - Ротатор с вязким затуханием и периодическим крутящим моментом

С помощью этой процедуры можно получить следующее точное отображение Пуанкаре для рассматриваемой системы:

Эти уравнения были впервые получены русским физиком Заславским при изучении нелинейного взаимодействия двух осцилляторов. В рассматриваемом механическом аналоге этой задачи величина у аналогична частоте отдельного осциллятора.Это двумерное отображение часто делают безразмерным посредством соотношений

Тогда при и уравнения принимают вид

где фигурные скобки {} обозначают, что берется только дробная часть выражения (т.е. mod 1 или ). Кроме того, здесь введены обозначения , и . Величиной измеряется отклонение скорости вращения от невозмущенного равновесного значения (рисунок 1.80 )

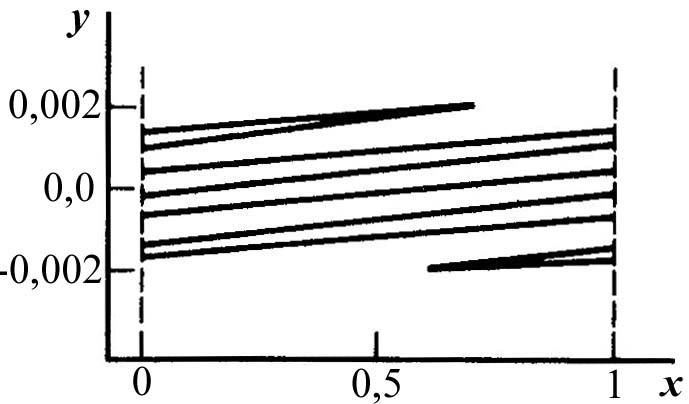
Рисунок 1.80 - Странный аттрактор отображения Заславского для подталкиваемого ротатора

Можно показать, что при малых эта система двух разностных уравнений имеет хаотические решения только при выполнении следующих условий: .

На рисунке показано типичное решение, полученное для значений параметров и .

Хаос в упругих непрерывных средах

Было проведено много экспериментов с хаотическими колебаниями упругих стержней. Исследованы проблемы двух типов.

В задачах одного класса уравнение в частных производных, описывающее движение стержня, линейно, но не линейны массовые силы или граничные условия. В других задачах движения достаточно сильны, чтобы в уравнениях движения стали существенными нелинейные члены.

При малых изгибах и отклонениях уравнение движения упругого

,

где – поперечное смещение стержня, – коэффициент упругой жесткости, – масса на единицу длины.

Правая часть уравнения описывает распределенные массовые силы или внутреннее затухание. Во многих опытах, для создания нелинейных массовых сил использовались постоянные магниты.

Когда смещение и наклон оси стержня велики, горизонтальное и вертикальное смещение и наклон характеризуются переменными , связанными соотношениями

.

где – длина, измеряемая вдоль деформированного стержня (см. рисунок).

Рисунок 1.81 - Плоская деформация упругого стержня

Уравнения сохранения импульса приобретают вид

,

где

.

В этих уравнениях – компоненты массовой силы, а – осевая сила, создающая напряжения в стержне. Нелинейные члены отличаются от характерных для механики жидкостей тем, что сюда не входят переносные, или кинематические, нелинейности. Локальная зависимость напряжений от деформации линейна. Нелинейные члены возникают из-за изменения геометрической формы и называются геометрическими нелинейностями.

Магнитоупругий изогнутый стержень

В этом примере упругий стержень, закрепленный с одной стороны, изгибается магнитами, которые помещены вблизи его свободного конца. Магнитные силы делают неустойчивым прямое, неизогнутое состояние стержня и создают несколько положений равновесия, одно из которых показано на рисунке 1.82.

Рисунок 1.82 - Упругий стальной стержень, изогнутый магнитными массовыми силами и прикрепленный к периодически движущемуся основанию

В экспериментах с помощью четырех магнитов создавалось до четырех положений устойчивого равновесия. После того как такой изгиб создан, система аналогична частице в потенциале из двух или более ям.

Устройство помещается на вибростенд и колеблется с постоянной амплитудой и частотой. При слабых колебаниях стержень остается вблизи одного из положений равновесия. С ростом амплитуды стержень может выскочить из потенциальной ямы и начинаются хаотические движения, при которых стержень переходит из одной ямы в другую

Для описания этой системы используется приближение со многими модами уравнения, в котором учтены нелинейные магнитные силы, действующие на свободный конец стержня.

Для стержня с затуханием, закрепленного с одной стороны, хорошие результаты дает приближение с одной модой. Соответствующее уравнение можно записать в виде системы трех уравнений первого порядка.

Обратите внимание, что здесь переменная является безразмерной амплитудой гармоники, а не расстоянием вдоль стержня:

Эта задача аналогична задаче о частице в паре потенциальных ям . Отображение Пуанкаре имеет вид, характерный для двумерных точечных отображений.

В типичных случаях эксперименты не обнаружили удвоений периода перед переходом к хаотическому движению. Предвестниками хаоса часто оказывались нечетные субгармоники.

Видоизменением этого эксперимента является перевернутый маятник с пружиной. Если пружина слабая, то, как и в задачах с двумя потенциальными ямами, перевернутый маятник имеет два положения устойчивого равновесия.

Изогнутый стержень с двумя степенями свободы

Чтобы изучить роль дополнительных степеней свободы, мы создали упругий аналог сферического маятника, в котором использован стержень кругового сечения.

Для изгибания стержня по-прежнему использовались магниты, но теперь его конец мог двигаться в двух направлениях. В результате появились несоизмеримые естественные частоты и квазипериодические колебания, которые в конце концов превратились в хаотические (рисунок 1.83).

Рисунок 1.83 - Схема упругого прута, совершающего трехмерные движения в паре потенциальных ям, созданных двумя магнитами

Эта экспериментальная модель описывается уравнениями для двух связанных осцилляторов:

,

Члены и описывают действие тяготения, если начальное положение стержня не вертикально, а члены, связывающие эти уравнения, потенциальны. Если связь слаба, можно решить уравнение относительно , и уравнение для приобретает вид уравнения параметрических колебаний.

Численные эксперименты с парой осцилляторов с затуханием и квадратичной связью, обнаруживают области хаотического движения, вызванного синусоидальным возбуждением. Рассмотривался частный случай, когда линейные собственные частоты и связаны соотношением .