3.8 Потеря устойчивости конструкций

Эксперименты с изгибаемым стержнем

Термин стержень употребляется для перевода нескольких различных английских слов: column, strut, beam, rod, поскольку им соответствует одна и та же математическая модель. Предположим, что мы заострили концы гибкой полоски длиной изготовленной из упругого металла или дерева, и сжимаем ее вдоль оси, используя нагружающее устройство, показанное на рисунке 1.33. Увеличивая медленно нагрузку , можно измерить отклонение центральной точки и изобразить зависимость от в виде графика. Вместо такого нагружения можно, конечно, использовать червячную передачу, чтобы фиксировать уменьшение длины стержня. Равновесные состояния тогда будут теми же самыми, однако область устойчивости изменится.

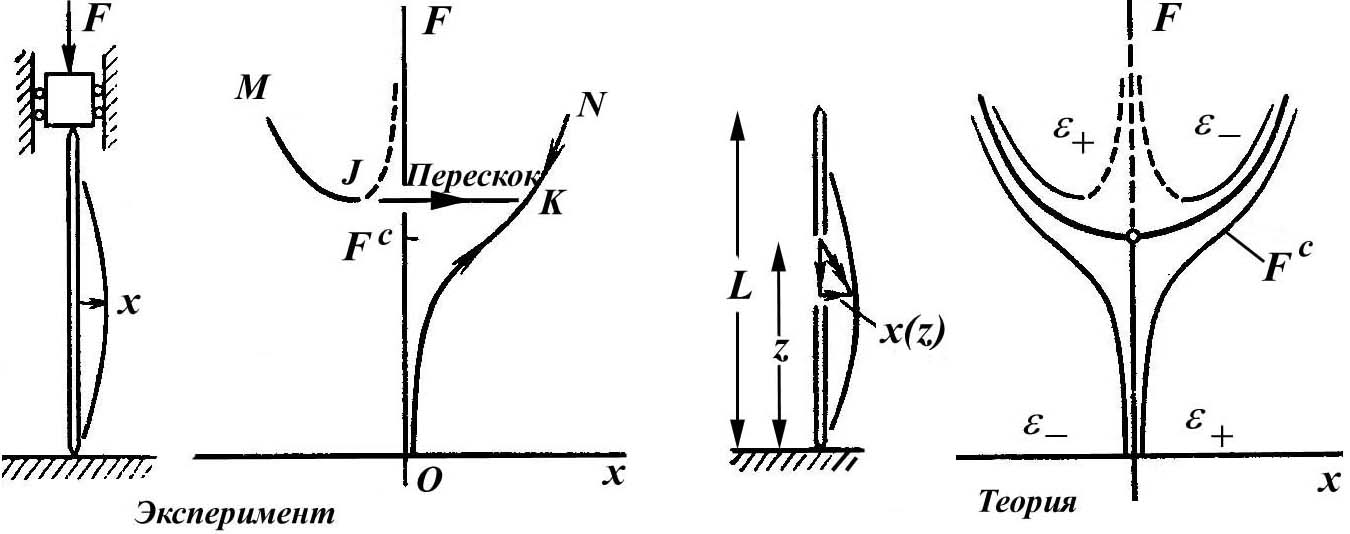
Рисунок 1.33 - Поведение сжатого стержня Эйлера (теория и эксперимент)

При нагружении стержня нагрузкой очень малые значения будут регистрироваться до тех пор, пока не приблизится к некоторому критическому значению . Как показывают наблюдения, вблизи этой нагрузки боковые отклонения быстро растут с ростом нагрузки. На рисунке зависимость от изображена кривой OKN.

Возрастание , связанное с потерей устойчивости, в дальнейшем замедляется в связи с увеличением жесткости системы в состоянии превышающим критическое. В точке N стержень находится в сильно изогнутом положении, подобном положению, в котором оказывается человек, опершийся на тростник. Несмотря на быстрый рост перемещения около точки , естественная траектория равновесия OKN везде устойчива, и движение вдоль нее гладко и обратимо (что отмечено стрелками на рисунке).

Говоря это, мы подразумевали, что разрушения материала не происходит и необратимых деформаций не возникает, так что поведение материала является упругим и стержень восстанавливает исходную прямую форму при снятии нагрузки.

Стержень может быть сильно изогнут в любом направлении, как с положительным, так и отрицательным значением . При высокой сжимающей нагрузке его можно привести во второе устойчивое состояние М, подталкивая в случае необходимости рукой.

Если затем разгружать стержень, то окажется, что в точке минимума J стержень перепрыгнет обратно в состояние К на естественной траектории нагрузки, при этом во время быстрого динамического хлопка не возникает изменения нагрузки. Последующие нагружение и разгрузка приведут к первоначально наблюдавшемуся гладкому естественному поведению. Скачок в предельной точке J представляет собой пример катастрофы складки.

Допустим, что мы хотим теперь смоделировать это поведение математически. Можно попытаться использовать простую инженерную теорию изгиба, в которой кривизна малого элемента стержня аппроксимируется величиной .

При этом – перемещение поперечного сечения, находящегося на расстоянии от нижней опоры в момент времени . Полагая, что кривизна пропорциональна изгибающему моменту, вычисленному в недеформированном состоянии (соответствующему нулевым перемещениям), найдем решение .

Это, конечно, правильный ответ для состояния равновесия идеально прямого стержня, однако он ничего не говорит нам об ожидаемой потере устойчивости.

Сжатие прямого упругого стержня понижает собственную частоту до тех пор, пока она, не станет равной нулю. Это происходит при значении нагрузки, равной критическому значению . Анализ линейных колебаний, в котором сохраняются только квадратичные члены энергии, показывает, что корень из основной собственной частоты для первой гармоники уменьшается до нуля по линейному закону при увеличении нагрузки до эйлеровой нагрузки потери устойчивости

.

Здесь – изгибная жесткость, которая представляет собой произведение модуля Юнга упругости материала на момент инерции поперечного сечения .

Эта критическая нагрузка, которая имеет фундаментальное значение в механике, может быть получена при помощи анализа потери устойчивости в рамках статики, если аппроксимировать кривизну по-прежнему выражением , но изгибающий момент в деформированном состоянии определить как . Результат такого линейного анализа соответствующей задачи на собственные значения предсказывает, что перемещение будет стремиться к бесконечности на некотором множестве критических нагрузок, соответствующих гармоническим перемещениям , где , причем наименьшая критическая нагрузка соответствует .

Полный нелинейный статический анализ закритического поведения, использующий более сложное точное выражение для кривизны, дает полную картину равновесия идеального стержня, которая была впервые найдена Эйлером (рисунок 1.34). Фрагмент этой картины для значений нагрузки, близких к , показан жирными линиями. Сплошными кривыми обозначаются устойчивые траектории деформации, а штрихами неустойчивые.

Чтобы добиться согласования с экспериментом, надо ввести в математическую модель наличия несовершенств, имеющиеся в стержне, такие, как, начальные отклонения его от прямолинейной формы. Эти несовершенства измеряют основное тривиальное решение, и траектория равновесия уже не проходит через точку бифуркации как показано на полной бифуркационной диаграмме. Здесь светлыми линиями представлены траектории равновесия двух систем, содержащих несовершенства, одна с положительным значением параметра несовершенства , другая с отрицательным значением .

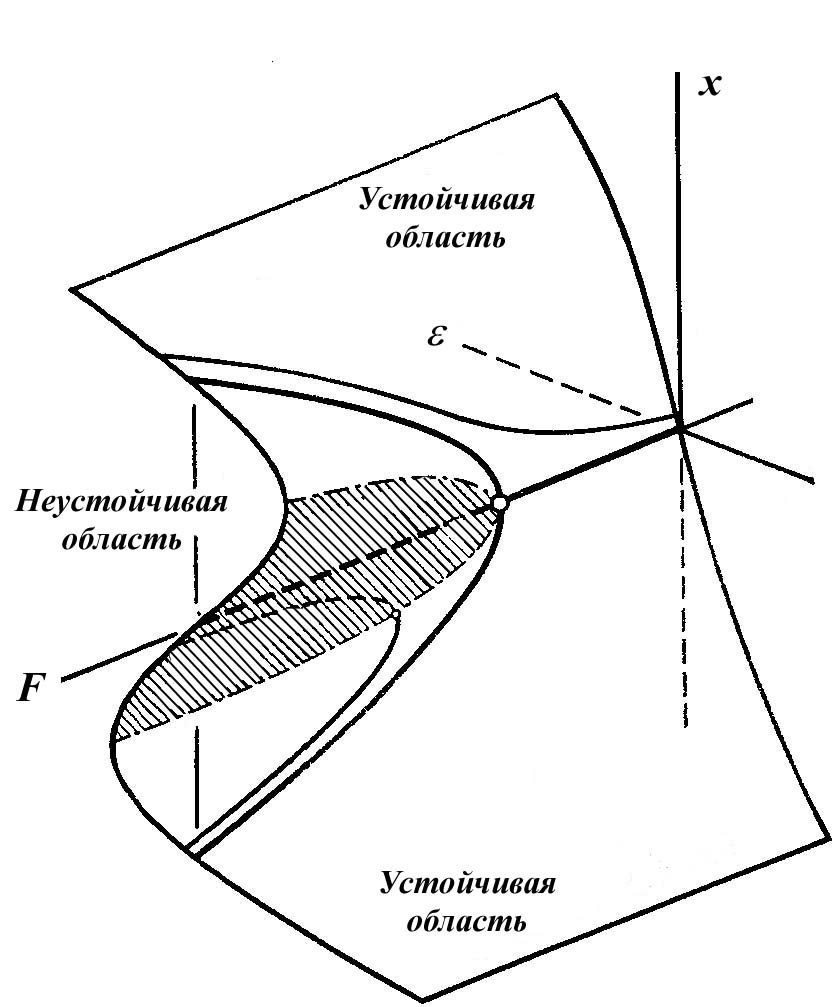
Рисунок 1.34 - Трехмерная картина траекторий равновесия

стержня в задаче Эйлера

По-прежнему сплошными и штриховыми кривыми показаны устойчивые и неустойчивые траектории соответственно.

Изобразим поверхность равновесия в трехмерном пространстве обобщенных координат – переменной состояния и двух управляющих параметров и . Видно, что устойчиво симметричная точка бифуркации стержня является катастрофой сборки.

Исследование модели консольного шарнира

Для иллюстрации некоторых основных идей рассмотрим модель шарнира, содержащую одну степень свободы. Шарнир, связанный с упругой пружиной, можно рассматривать как простейшую модель стержня, закрепленного на одном конце (качественно он ведет себя как нижняя часть шарнирно опертого стержня).

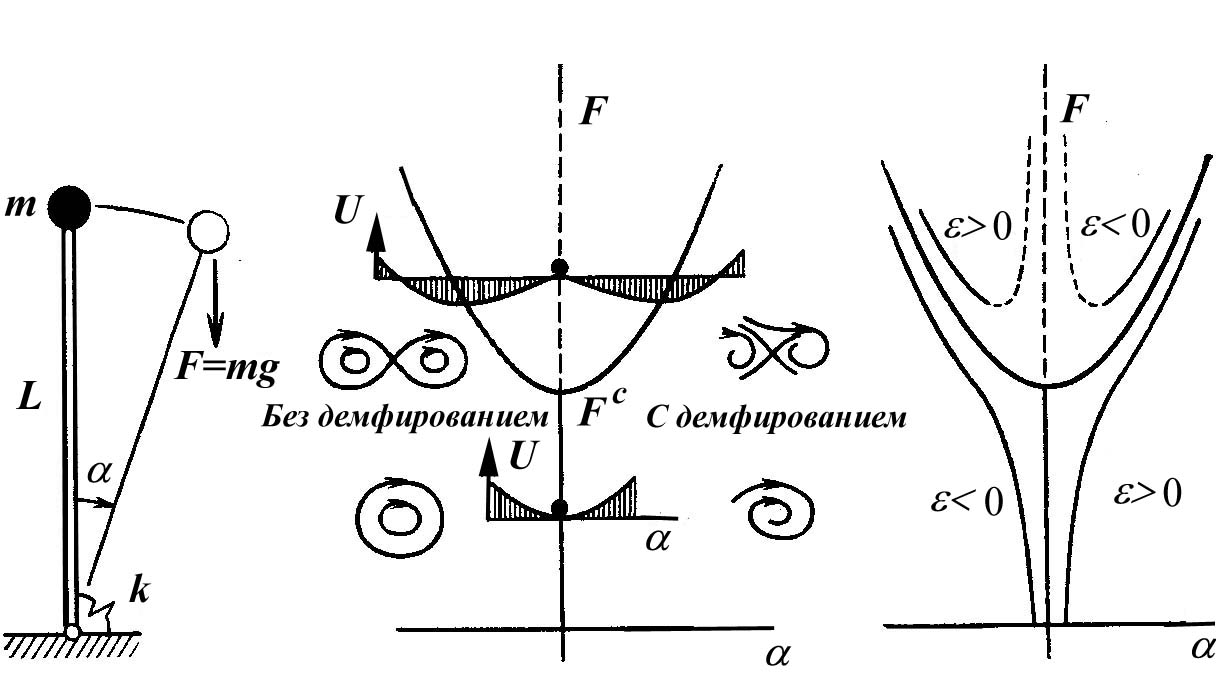
Рисунок 1.35 - Статическое и динамическое поведение шарнирно опертого стержня с круговой пружиной

Рассмотрим невесомый недеформируемый стержень длиной , соединенный с упругой пружиной жесткости (см. рисунок). Пружина сопротивляется вращению стержня. Стержень несет точечную массу на конце и находится в постоянном гравитационном поле с ускорением , что означает, что консоль находится под действием силы величиной . Мы будем рассматривать как управляющий параметр нагружения и будем исследовать потерю устойчивости системы по мере того, как постепенно увеличивается от нулевого значения.

Выберем в качестве обобщенной координаты угол поворота от вертикали и проведем сначала статический анализ.

Энергия деформации, накопленная в пружине, есть

,

а расстояние, на которое опустилась масса т, вычисляется по формуле .

Общая потенциальная энергия системы дается равенством

Уравнение равновесия

.

имеет тривиальное решение для всех и решение, определяемое из уравнения

Имеются две траектории равновесия. Они обозначены на рисунке жирными линиями. Устойчивость равновесных состояний определяется выражением

.

Вдоль основной «тривиальной» траектории равновесия устойчивость имеет место при , меньшем , а неустойчивость – при , большем , где . Предположим, что вал вращается с некоторой угловой частотой , тогда выражение для силы будет иметь следующий вид .

Для устойчивого равновесного состояния имеем

и устойчивость имеет место при следующем критическом значении равном

.

Аналогичным образом находятся устойчивые траектории равновесия в состоянии, превышающим критическое. Общая потенциальная энергия имеет единственный минимум для заданного и два минимума, разделенных максимумом, для каждого . Это схематически показано на рисунке.

Динамику системы в рамках нелинейной теории легко найти качественно при помощи графиков общей потенциальной энергии системы. Если пренебречь демпфированием, то центр, соответствующий тривиальному состоянию для , будет трансформироваться в два центра, разделенных седлом, для . Если имеется некоторая положительная вязкость, то устойчивый фокус в тривиальном состоянии для будет переходить в два устойчивых фокуса, разделенных седлом, как показано на рисунке для .

Мы не будем исследовать эти нелинейные движения и вместо этого рассмотрим линейные колебания около состояния равновесия . Будем считать, что стержень невесом. Тогда кинетическая энергия системы сводится к кинетической энергии точечной массы и дается формулой

.

Сравнивая ее с общим выражением для кинетической энергии

имеем . Угловая частота малых колебаний тогда дается теорией линейного осциллятора в виде

Эта частота уменьшается до нуля, когда возрастает до . Мы видим, что имеются три различных пути для определения критической нагрузки :

1. ветвление тривиальной траектории равновесия;

2. исчезновение минимума потенциальной энергии;

3. обращение в нуль частоты колебаний.

Эквивалентность (1) и (2) гарантируется основной теоремой теории упругой устойчивости. Эквивалентность (2) и (3) установлена для общих консервативных механических систем, в которых дополнительно учитывается малая вязкость.

В заключение рассмотрим влияние начальных геометрических несовершенств на изменение траектории статического равновесия системы. Предположим, что в силу небольшой технологической ошибки пружина находится в недеформированном состоянии не тогда, когда стержень вертикален, а когда он наклонен по отношению к вертикали на малый начальный угол . Общая потенциальная энергия системы с точностью до произвольной постоянной имеет теперь вид

,

поэтому для равновесия получим

,

что приводит к равенству

.

Видно, что траектория тривиального равновесия переходит в семейство равновесных кривых , соответствующих различным значениям и окружающих бифуркационные кривые идеальной системы, как показано на рисунке.

Модель стержня с одним шарниром

Изучим поведение стержня с точки зрения теории катастроф. Заменим наш стержень системой из двух жестких стержней шарнирными соединениями в точках А, В, С и пружиной в В, которая стремиться выпрямить шатуны в одну линию. Если пружина линейна, она создаст усилие , пропорциональное углу , и будет обладать потенциальной энергией , где – постоянная упругости пружины.

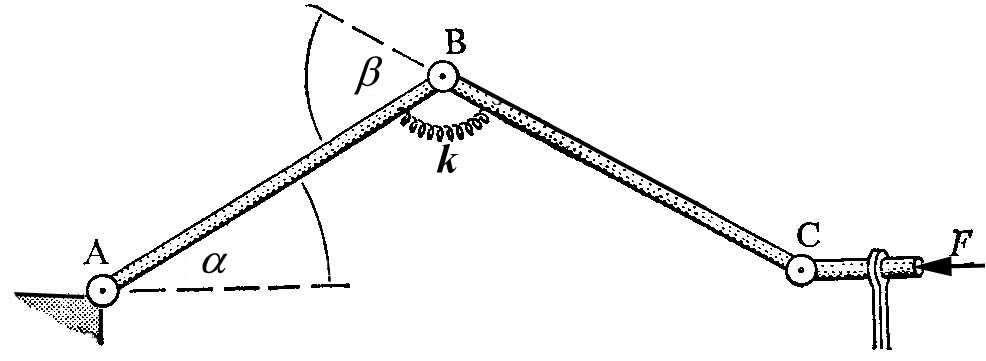
Рисунок 1.36 - Конечно-элементная модель стержня (2 стержня с пружиной)

Допустим, что каждое колено (шатун) имеет длину равную 1. Суммируя потенциальную энергию пружины и потенциальную энергию, отвечающую положению силы , мы получим полную энергию (с точностью до константы)

.

Воспользуемся разложением в ряд Тейлора до четвертого порядка точности. В результате получим

.

откуда

.

Когда меньше , имеет минимум при (и нетрудно увидеть, что это единственный минимум).

Когда , имеет вырожденный минимум, в котором немедленно узнается точка стандартной сборки, так как коэффициент при положителен.

Проводя через значение , скажем полагая , мы получим деформацию

.

Она универсальна среди четных функций (хотя мы и не дали алгебры, нужной для установления этого факта), и в действительности деформация исходной функции U сильно эквивалентна вблизи интересующей нас точки деформации диаграмма катастрофы для которой представлена на рисунке, а.

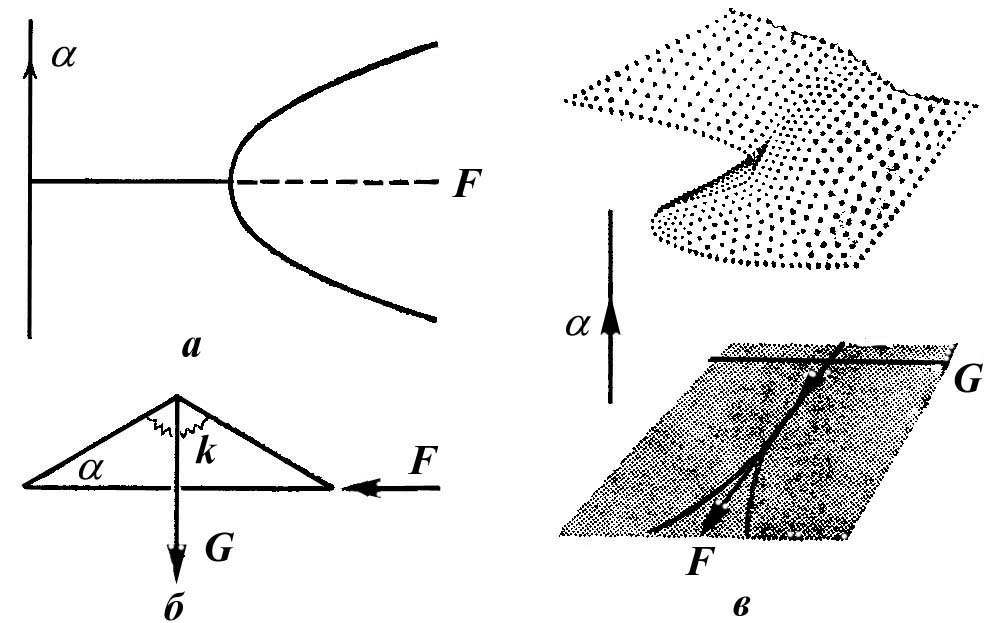
Рисунок 1.37 - Катастрофа сборки для модели стержня с одним шарниром

Но симметрия является здесь, неприемлемой как абсолютное ограничение, введение же почти любой асимметричной силы (рисунок 1.37 б) приводит нас к обычной картине сборки (рисунок 1.37 в). Для силы G такой, как показано на рисунке, имеем

так что

,

или

.

Отсюда следует, что U сильно эквивалентна

,

а это, с точностью до линейной замены, стандартная сборка.

В отличие от рассмотренного выше симметричного случая это описание структурно устойчиво. Возмутим функцию , заменив ее на , где – любая функция от и каких угодно других управляющих параметров, включенных в описание системы (разность длин шатунов, боковые смещения нагрузки , угол между и перпендикуляром к ). Тогда при малых значениях и прочих дополнительных параметров сохраняется не только та же картинка, но и та же формула, с точностью до гладкой замены переменных. Точка острия, направление острия и прочие параметры перемещаются плавно с изменением и дополнительных параметров. Это – следствие универсальности трансверсальных деформаций и устойчивости трансверсальности.

Модель стержня с двумя степенями свободы

Прежде чем приступить к анализу стержня со многими модами, рассмотрим модель трехзвенного шарнирно опертого стержня, который имеет две степени свободы. Этот стержень в деформированном состоянии изображен на рисунок 8.6.

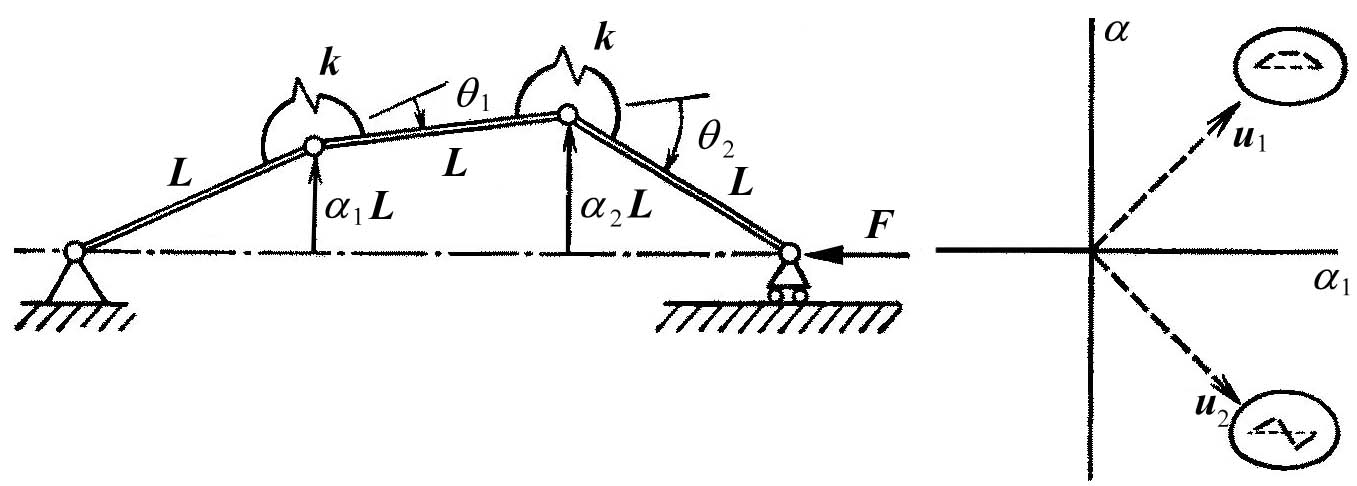
Рисунок 1.38 - Перемещения и моды в модели стержня с двумя шарнирами

Он состоит из трех стержней длиной , соединенных шарнирами и образующих цепь длиной . Краевое звено цепи вращается вокруг фиксированной точки, а второе звено может свободно вращаться вокруг краевого звена. При относительном вращении стержней в точках соединений возникает сопротивление со стороны двух круговых пружин, каждая из них имеет жесткость . Пружины находятся в недеформированном состоянии, когда стержни лежат на прямой линии, так что при отсутствии нагрузки стержни находятся на прямой горизонтальной линии между опорами. Система нагружается мертвой сжимающей нагрузкой , которая по предположению сохраняет свое первоначальное значение и направление при деформировании шарниров.Система имеет две степени свободы. Вертикальные смещения точек соединения обозначаются через и , как показано на рисунке, так что общее деформированное состояние системы может быть полностью описано безразмерными обобщенными координатами и . Обе они равны нулю в недеформированном состоянии системы.

Энергия деформации, накапливаемая в двух круговых пружинах, дается формулой

,

которая может быть переписана в виде

.

Раскладывая каждый из тригонометрических членов в ряд по и , имеем

+ члены высшего порядка малости).

Укорочение стержня, вызванное поперечным перемещением точек сопряжения, дается равенством

.

Раскладывая снова в степенной ряд, имеем высшего порядка малости). Общая потенциальная энергия системы есть . Последний член представляет потенциальную энергию приложенной нагрузки. Вторая вариация потенциальной энергии равна

.

Это та самая квадратичная форма, которую нужно исследовать для изучения устойчивости прямой конфигурации. Прямая конфигурация является равновесным состоянием, поскольку в разложении потенциальной энергии отсутствуют линейные члены и первая вариация равна нулю.

В рассматриваемой задаче квадратичная форма энергии деформации пружин положительно определена, так как она выведена из выражения, состоящего из суммы двух квадратов. Если имеются две квадратичные формы и одна из них положительно определена, всегда можно найти линейную замену переменных, которая одновременно приводит две формы к диагональному виду. В нашей задаче это достигается невырожденным преобразованием

,

которое имеет следующее обращение:

Чтобы понять, как расположены новые оси ; в -пространстве, заметим, что при и при . Поэтому оси координат , ортогональны и повернуты на угол 45° по отношению к осям координат как показано на рисунке.

В терминах главных координат прямой подстановкой находим

.

Сравнивая это выражение с суммой квадратов в стандартной форме

,

получаем коэффициенты устойчивости

.

Если приложенная нагрузка равна нулю, то прямая конфигурация устойчива, поскольку

,

и энергия имеет локальный минимум, как показано внизу справа на рисунке. Показаны энергетические поверхности для различных значений нагрузки.

По мере увеличения осевой сжимающей нагрузки два коэффициента устойчивости уменьшаются по линейному закону до тех пор, пока не достигнет значения, равного нулю, которое соответствует первой критической нагрузке , даваемой равенством . При этой нагрузке кривизна поверхности энергии в направлении уменьшается до нуля, так что вторая вариация имеет цилиндрическую форму, показанную справа на рисунке 1.39. Говорят, что стержень теряет устойчивость по моде при этой критической нагрузке.

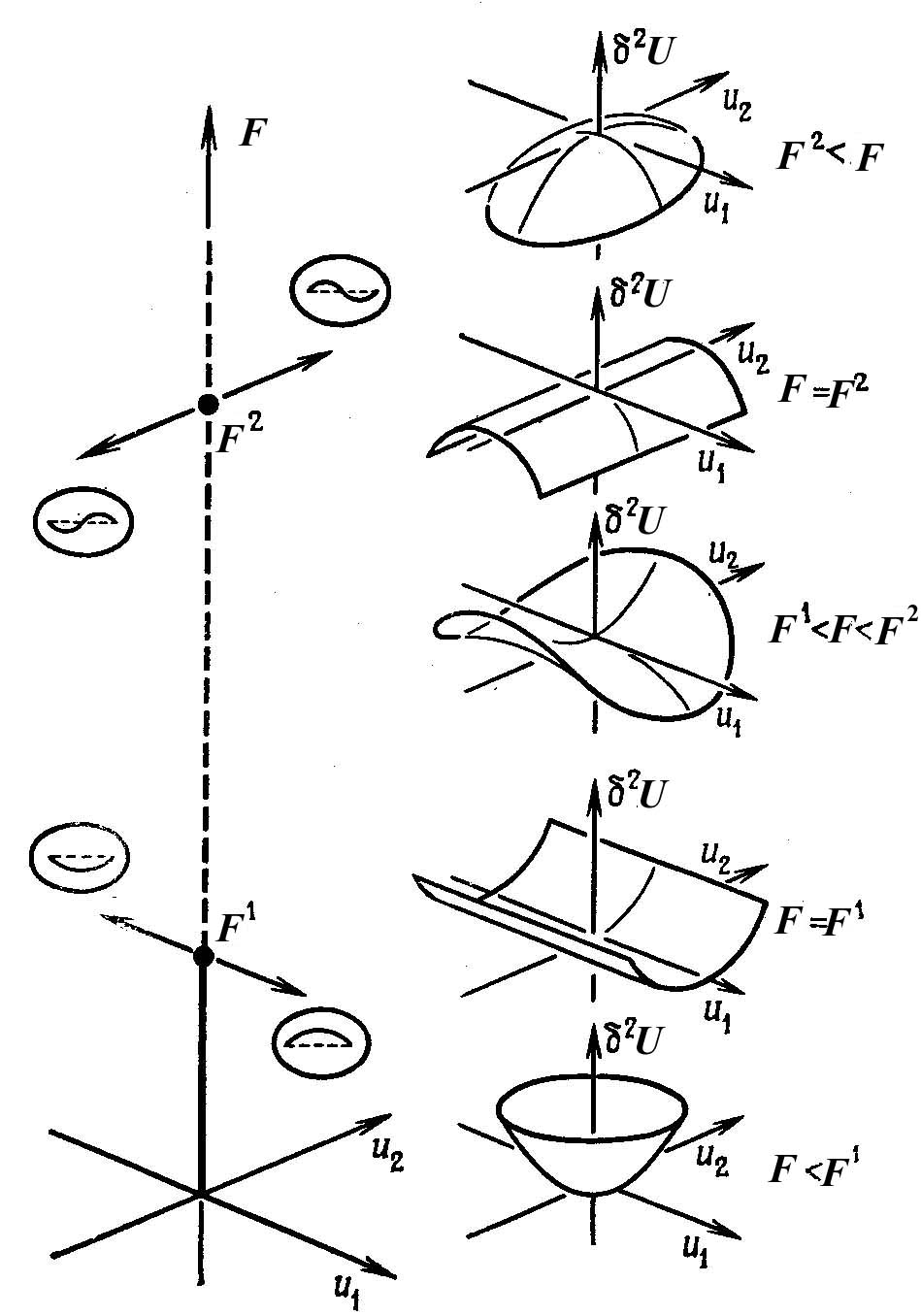
Рисунок 1.39 - Трехмерная диаграмма нагрузка-перемещение в линейной теории шарнирно опертого стержня

Если нагрузка превысила значение , коэффициент становится отрицательным, в то время как коэффициент остается пока положительным. Поверхность второй вариации энергии имеет теперь форму седловой точки, загибающейся вверх в направлении координаты и вниз в направлении координаты , как показано на рисунке. Прямая основная конфигурация системы теперь является неустойчивой. Можно сообщить больше информации, если сказать, что прямая конфигурация неустойчива по отношению к , но устойчива по отношению к .

Если мы продолжаем увеличивать приложенную нагрузку , второй коэффициент устойчивости , достигнет, наконец, нулевого значения, когда нагрузка становится равной второму критическому значению , даваемому формулой .

При этой второй потере устойчивости вторая вариация энергии снова изображается цилиндрической поверхностью, как показано на рисунке, а для достаточно больших значений нагрузки она имеет локальный максимум.

Можно сказать, что в модели стержня происходит потеря устойчивости по моде при второй критической нагрузке , хотя это условие не может быть достигнуто экспериментально без наложения дополнительных ограничений, исключающих более раннюю потерю устойчивости по моде .

Подчеркнем, что каждая поверхность энергии, изображенная в правой части рисунка 1.40 соответствует заданному фиксированному значению приложенной нагрузки .

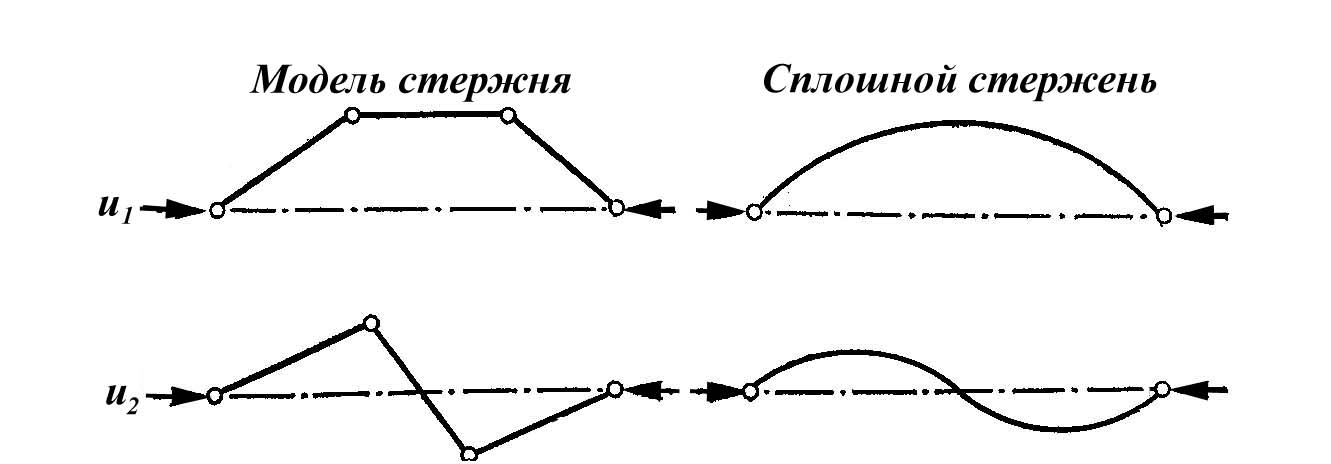
Рисунок 1.40 Моды потери устойчивости в модельной задаче о реальном сплошном стержне

Легко охарактеризовать деформации системы в терминах . Когда речь идет о моде , то подразумевается деформация, которая происходит при . Равенство означает, согласно формулам перехода к старым переменным, что , так что мода соответствует симметричной деформации, аппроксимирующей первую гармонику сплошного стержня, как показано на рисунке. Аналогично равенство означает, что , так что мода соответствует антисимметричной деформации, аппроксимирующей вторую гармонику сплошного стержня, как показано на рисунке1.40.

Исследование, подобное проведенному и имеющее целью определить критические нагрузки при помощи изучения второй вариации потенциальной энергии , называют линейным анализом собственных значений. Оно не добавляет новой информации о поведении системы после начального момента потери устойчивости, которое управляется слагаемыми энергии, имеющими в состоянии критического равновесия более высокий порядок малости.

Полный гармонический анализ стержня на упругом основании

Дополним этот короткий аналитический экскурс в теорию устойчивости многомодовым линейным гармоническим анализом шарнирно опертого стержня, который взаимодействует (или не взаимодействует) с упругим основанием. Упругое основание действует поперек оси стержня и может быть реализовано как пружинящая подложка, на которой горизонтально лежит стержень. Упругое основание можно представлять себе как большое число упругих пружин, сопротивляющихся поперечным перемещениям .

Линеаризованное выражение для энергии, которое требуется в теории колебаний с малой амплитудой и для анализа устойчивости упругого стержня, следует из приведенных выше формул. Энергия деформации изгиба есть

,

потенциальная энергия мертвой осевой сжимающей нагрузки есть

,

а энергию деформации простого упругого основания, на котором находится стержень, можно записать в виде

,

где – жесткость основания. Итак, общая потенциальная энергия может быть записана в форме

.

Кинетическая энергия дается равенством

.

Уравнение колебания стержня имеет вид

.

Можно показать, что в случае дискретной модели уравнение для малых колебаний стержня имеет вид

.

И для диагональных коэффициентов энергии имеем

.

Поэтому угловая частота для -й моды дается равенством

.

Величины суть собственные частоты колебаний шарнирно опертого упругого стержня с массой на единицу длины и изгибной жесткостью , покоящегося на упругом основании жесткости и несущего осевую сжимающую нагрузку . Если положить равными нулю (или, что эквивалентно, равными нулю), то получатся критические нагрузки потери устойчивости системы

.

Критические нагрузки для шарнирно опертого стержня, не взаимодействующего с основанием, соответствуют нулевому значению

.

Наименьшая из этих критических нагрузок есть

.

Видно, что для стержня на основании с жесткостью первая гармоника ( ) не всегда соответствует наименьшей нагрузке потери устойчивости, как показано на рисунке. По оси ординат отложена приведенная нагрузка , а по оси абцис приведенная жесткость .

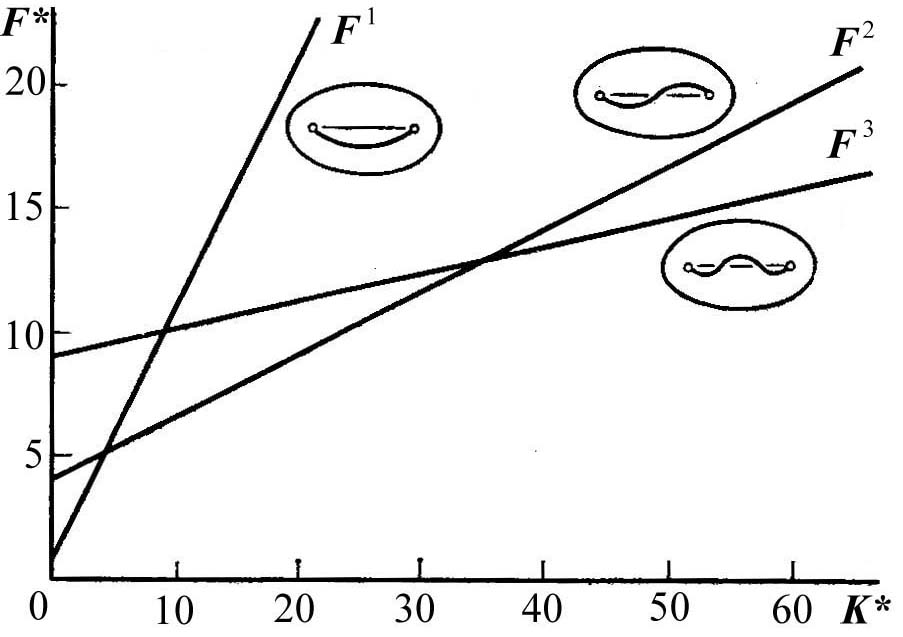
Рисунок 1.41 - Критические нагрузки для стержня на упругом основании в зависимости от меры жесткости основания

Если положить жесткость основания и изгибную жесткость равными нулю ( ) и написать , то получим формулу для собственной частоты колебаний струны, растягиваемой усилием :

.