3.7 Устойчивость и теория катастроф

Классическая физика (от Ньютона до общей теории относительности) – это по существу теория плавного поведения. Первый, приходящий в голову пример – движение планет вокруг Солнца, внушающее трепет своей непрерывностью, неторопливостью и чрезвычайной регулярностью. Даже колебания земной оси, из-за которых пришлось отказаться от вращения Земли как от эталонных часов, и те происходят плавно. Но изменения совершаются и скачками. Вдруг закипает вода. Начинает таять лед. Сотрясаются земли и луны. Рушатся дома. Происходят биржевые крахи.

Такого рода изменения гораздо хуже поддаются анализу и предсказанию, чем движение небесных тел, и различные науки (от физики до экономики) еще только накапливают аналитические средства, которые бы им позволили управляться со скачкообразным поведением.

Природа скачков бывает самой различной. Есть силы, которые постепенно нарастают до тех пор, пока их уже больше не может сдержать трение. Есть критическая плотность популяции, ниже которой особи развиваются как кузнечики, а выше – как саранча. Вот почему, если саранча появляется, она появляется тучей.

Многое здесь еще не поддается анализу. Многое уже проанализировано, причем применялось великое множество математических методов. В этой главе мы будем иметь дело с одним математическим подходом, в рамки которого единообразно укладывается обширная область явлений такого рода.

Методы, которые при этом используются, были развиты французским математиком Ренэ Томом и стали широко известными благодаря его книге «Структурная устойчивость и морфогенез», где они были предложены в качестве математической основы для биологии.

Катастрофы, что это такое? Те внезапные изменения, о которых тут идет речь, были окрещены Томом катастрофами, для того чтобы выразить ощущение резкой перемены. Это слово, к сожалению, несет в своем значении оттенок бедствия, который в большинстве приложений неуместен. Но весь предмет с тех пор получил известность как теория катастроф – словосочетание, дающее большую свободу толкования, в зависимости от принятой точки зрения.

Эти методы наиболее применимы к системам, в которых в каждый момент на фоне изменяющейся ситуации минимизируется некоторая функция, например, энергия или энтропия соответственно. Хорошим примером служит шарик, катящийся по неровной поверхности. Он «старается» при посредстве силы тяжести найти положение, если и не самое низкое из всех возможных, то хотя бы самое низкое из всех других поблизости. Тем временем меняется и сама поверхность.

Те специальные геометрические образования, которые возникают при такой постановке задачи, называют элементарными катастрофами, имея в виду элементы как фундаментальные сущности (подобно химическим элементам); их применением, занимается элементарная теория катастроф. В смысле, аналогичном «элементарной арифметике. Для некоторых систем могут происходить более сложные вещи, которые классифицируются как обобщенные катастрофы.

Машина катастроф Зимана. Мы начнем с машины, изобретенной первой. Ее придумал в 1969 г. Э. К. Зиман из Уорикского университета. Поэкспериментировав недели три с резиновыми полосками и канцелярскими скрепками, он усовершенствовал первоначальную идею до того варианта, который излагается ниже.

Основной частью машины является лежащее на доске колесико (рисунок 1.25), которое может свободно вращаться вокруг своей оси. Оно должно быть не слишком тяжелым: если трение, замедляющее движение, или инерция, поддерживающая его, окажутся слишком большими, то это затемнит как раз те черты в поведении колесика, которые нас интересуют.

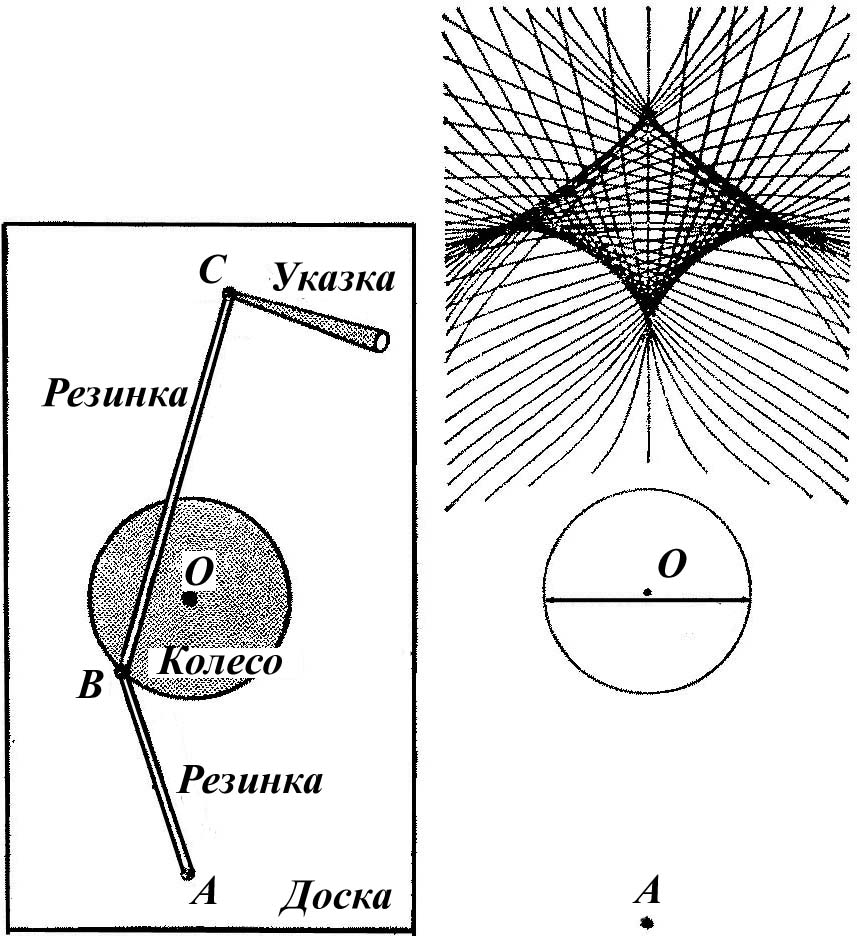
Рисунок 1.25 - Машина Зимана

К точке В на краю колесика прикрепляются две резинки. Второй конец из них закреплен на доске в точке А достаточно далеко от центра О колесика таким образом, чтобы резинка ВА всегда была натянутой. Второй конец другой резинки (точка С) прикрепляется к указке, которую держат в руке. Благодаря этому возможно управлять концом С с небольшого расстояния, не заслоняя его от себя. Удобен такой выбор размеров: радиус колесика 3 см, длина отрезка АО 12 см, длина каждой резинки 6 см.

Независимо от того, как выбраны радиус колесика, длины и резинок ВА и ВС (в нерастянутом состоянии) и расстояние ОА (лишь бы оно было больше, чем ), качественная картина явления неизменной.

В этом факте проявляется свойство «структурной устойчивости», когда изменения параметров не приводит к существенным качественным изменениям в поведении системы. Тем не менее, мы будем иметь в виду машину, для которой приняты определенные размеры.

Если конец указки С, держа его на одной высоте с А над доской, помещать над точками, лежащими вне четырехугольной области <> (см. рисунок), то колесико под действием резинок останавливается лишь в одном положении. Если вы повернете его в другое положение и отпустите, то оно «прыгнет» обратно. Это единственное положение зависит от С, и плавное перемещение С приводит к плавному изменению положения колесика.

Если же ввести конец указки внутрь области <>, то оказываются возможными два положения равновесия. При плавном входе в область <> с одной стороны колесико плавно приходит в одно из этих положений. При входе с другой стороны колесико после подведения конца указки С к той же точке окажется в другом из двух возможных положений.

Лишь если вы чисто умозрительно сможете решать, что произойдет, если ввести указку слева через верхнюю или нижнюю сторону области <> и вывести ее затем направо через верхнюю или нижнюю сторону (всего четыре возможности), вам не нужно изготавливать машину, чтобы понять, как она работает.

Методы теории катастроф

Проанализируем поведение машины Зимана для тех конкретных размеров, которые были указаны выше. Изменение размеров не внесет серьезных качественных отличий в поведение, – факт, в котором в зародыше содержится важная идея, развиваемая нами в полной мере позднее.

Первый шаг состоит в том, чтобы определить положение точки острия Р. В силу соображений симметрии эта точка лежит на оси (рисунок 1.26). Возьмем в качестве единицы длины диаметр диска, так что длины нерастянутых резинок равны 1, а расстояние ОА равно 2.

Снова по симметрии ясно, что когда точка В перемещается вдоль оси, всегда имеется положение равновесия, отвечающее .

Точка Р находится там, где равновесие меняется с устойчивого (локальный минимум энергии) на неустойчивое (локальный максимум).

Пусть и обозначают длины наших двух резинок в положении, когда диск повернут на угол , близкий к нулю, но необязательно равный нулю. По закону Гука энергия системы равна

,

где – модуль упругости резинок.

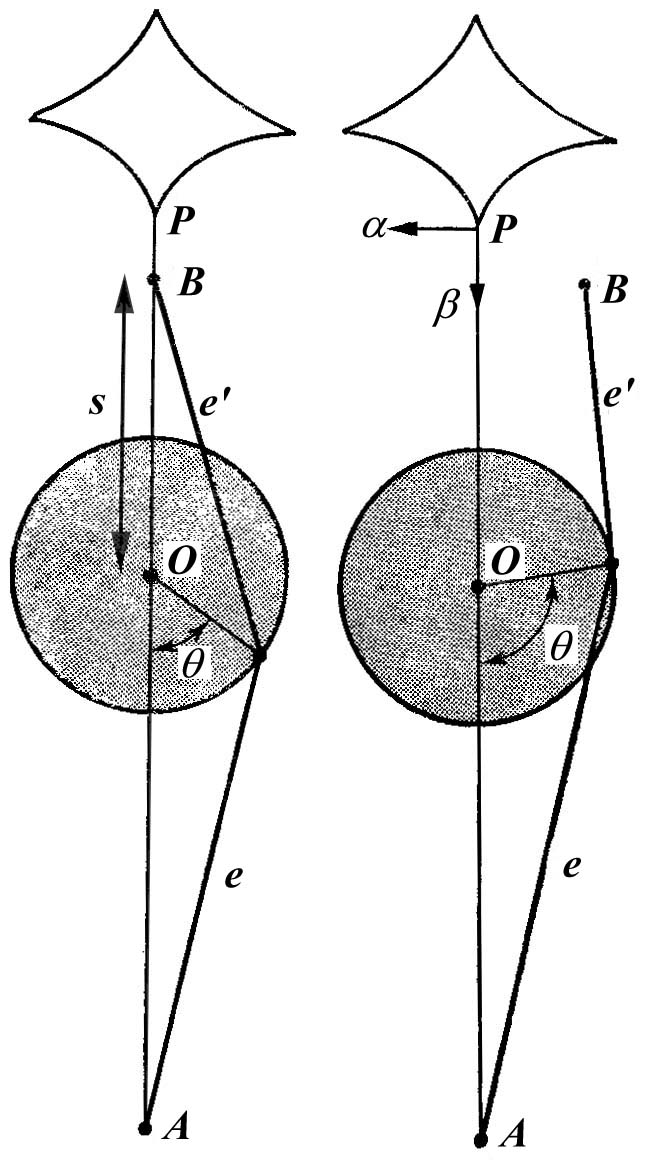
Рисунок 1.26 - К анализу работы машина Зимана

Далее,

,

и, беря разложение в ряд Тейлора, мы найдем, что

где обозначает функцию порядка 4.

Упрощая, получаем

(мы включили члены с в ). Следовательно,

.

Аналогично

.

Значит,

.

Мы можем пренебречь членом , если коэффициент при отличен от нуля. Но коэффициент при в нашем случае

положителен, если ,

отрицателен, если .

Изменение от минимума энергии к максимуму наблюдается там, где

или

.

Решения этого уравнения таковы:

ясно, что точка Р отвечает положительному значению , т. е.

Аналогичное рассуждение с заменой на позволяет определить положение верхнего клюва Р', для которого получаем

Можно определить и положение двух боковых клювов, но анализ в этом случае сложнее.

Проведем анализ поведения колеса вблизи точки Р. Член в энергии исчезает в точке Р.

В силу симметрии член с также отсутствует, так что мы должны обратиться к члену с . Далее мы работаем с рисунком б.

Пусть свободный конец В находится в точке относительно указанной на рисунке системы координат (оси взяты с направлениями, противоположными обычным, из соображений алгебраического удобства).

Формула для получается та же, что и раньше, только теперь мы работаем с точностью до и сохраняем члены с , а для имеем формулу

.

Беря разложение соответствующей функции энергии с точностью до членов пятого порядка, получаем выражение вида

.

Здесь – некоторые константы, точное значение которых не имеет большого значения; приблизительно они равны

, , , ,

В точке Р, где , мы имеем функцию вида . При получении качественных результатов для точки Р мы можем пренебречь членом .

Мы можем упростить выражение для функции энергии, отбросив член . Дальнейшие упрощения достигаются таким выбором единиц для физических величин, чтобы , устранением кубического члена при помощи замены

;

введением вместо и их подходящих скалярных кратных и соответственно (численно они оказываются равными примерно и ). Это приводит к следующему выражению для энергии: с некоторой постоянной с.

Так как нас интересуют только критические точки , мы можем без потери общности взять (или перенести начало отсчета значений энергии). В результате приходим к выражению вида

Этой формулой определяется то, что позже мы назовем катастрофой сборки.

Наш следующий шаг, на котором фактически и будет получена полезная информация, состоит в анализе критических точек .

Каноническая катастрофа сборки

Проведем анализу структуры критических точек функции .Для заданной пары критические точки функции определяются из условия

Дроби в коэффициентах подбирались как раз так, чтобы получилось уравнение простейшего вида.

Это уравнение кубическое по , и поэтому оно имеет самое большее три и самое меньшее один вещественный корень.

Природа корней зависит от значений и , a именно от дискриминанта рассматриваемого кубического уравнения.

Если , имеются три различных вещественных корня, а если , то один вещественный и пара взаимно сопряженных комплексных корней. Если , то имеются три вещественных корня, но некоторые из них совпадают между собой: если , но или , то совпадают два корня, а если и , то совпадают все три корня.

Геометрически это означает, что природа корней, а значит и равновесие машины, зависит от положения свободного конца резинки по отношению к кривой, определяемой в координатах уравнением .

На рисунке 1.27 она изображена жирной линией.

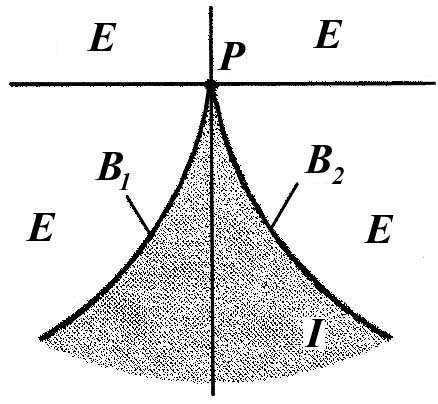
Рисунок 1.27 - Кривая, описываемая уравнениеем

Подразделим плоскость (обозначим ее через С) на пять подмножеств:

• заштрихованную область «внутри» кривой;

• область «вне» ее;

• две ветви и кривой и начало Р.

Точки , лежащие в , характеризуются условием , а точки, лежащие в , условием .

Поэтому:

если лежит в , то имеется один вещественный корень;

если лежит в , то имеются три различных вещественных корня;

если лежит в или в , то имеются три вещественных корня, но два из них совпадают между собой. Для совпадение происходит с наименьшим корнем, а для – с наибольшим;

если совпадает с , т. е. , то имеются три совпадающих вещественных корня (все они равны 0).

Эти возможности проиллюстрированы на рис. 7.4 а. Вид соответствующих потенциальных функций (7.1) показан на рис. 7.4, б.

Мы видим, что имеет один минимум, если , два минимума и между ними максимум, если , один минимум и одну точку перегиба для или и один минимум для .

В последнем случае потенциальная функция есть и потому этот минимум более сложный с математической точки зрения, чем предыдущие. Здесь равны нулю первые три производные функции , тогда как во всех остальных случаях равна нулю только первая производная. Это отвечает трем совпадающим корням кубики для .

Отметим также, в чем состоит различие между потенциальными функциями точек , лежащих на ветвях и : для точка перегиба лежит слева от минимума, а для – справа (рисунок 1.28).

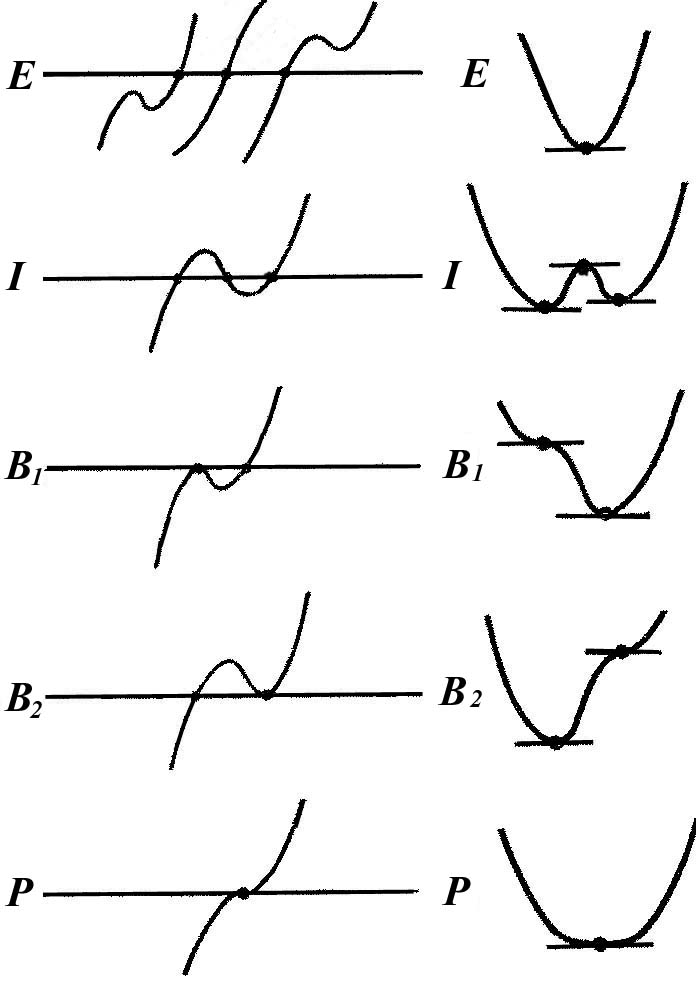
а б

Рисунок 1.28 - Возможные критические точки

потенциальной функции – а, и ее вид – б

С точки зрения динамики минимумы отвечают устойчивым равновесиям, а максимумы или перегибы – неустойчивым. Итак, если наша пара управляющих параметров лежит в , то имеется единственное положение устойчивого равновесия, а если в , то имеются два устойчивых положения и одно неустойчивое.

Это довольно сложное поведение потенциальной функции можно охватить единой геометрической картинкой, делающей всё чрезвычайно наглядным, нарисовав многообразие катастрофы, или поверхность равновесия, в пространстве .

Это – множество точек , удовлетворяющих уравнению, которое мы здесь перепишем так .

Оно имеет вид поверхности со сборкой и показано на рисунке 1.29.

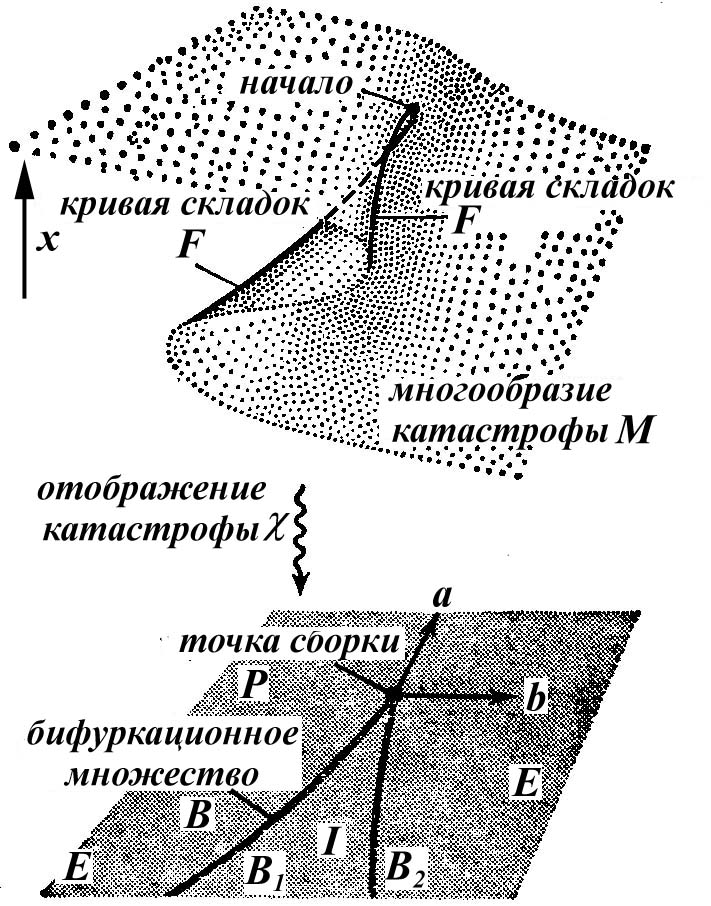
Рисунок 1.29 - Катастрофа складки Машины Зимана и ее отображение

Теперь мы в состоянии дать геометрическую интерпретацию положений равновесия соответствующей динамической системы.

Для данной пары значений параметров положения равновесия получаются решением уравнения (7.2). Они могут быть, следовательно, описаны как -координаты тех точек, в которых вертикальная прямая, проходящая через , пересекает многообразие катастрофы.

Геометрически очевидно, что если лежит в области , внешней по отношению к бифуркационному множеству , то найдется лишь одно такое ; действительно, над точками лежит лишь один лист поверхности.

В то же время над точками области расположены три листа и соответственно имеется три положения равновесия.

Для точки вертикальная прямая, проходящая через , касательна к нижнему листу и проходит через верхний лист в единственной точке; это дает для уравнения (7.2) два совпадающих корня и еще один, причем совпадающие корни меньше.

Для всё аналогично, только теперь имеет место касание верхнего листа и совпадающие корни больше. Наконец, в точке острия вертикальная прямая касается поверхности и пересекает ее в одной-единственной точке – в начале.

Итак, при геометрическом описании состояний равновесия почти всё становится совершенно очевидным. Чтобы закончить картину, необходимо только различить устойчивые и неустойчивые положения равновесия. Неустойчивые отвечают точкам поверхности, лежащим на среднем листе, внутри кривой складок. Устойчивые – точкам снаружи кривой складок.

Динамика машины Зимана

Заголовок этого параграфа может ввести в заблуждение: мы рассматриваем здесь на самом деле статику машины – положения равновесия. Полное ее динамическое описание (что произойдет, если мы крутанем колесо, дернем за резинки нити и т. п.) выходит за рамки рассмотрении, проводимых в этой книге, и принадлежит полнокровной теории динамических систем. Мы займемся тем, что иногда называют квазистатикой: что происходит с положениями равновесия при плавном изменении положения свободного конца резинки?

Экспериментально этому отвечает очень медленная динамика. Дело в том, что машина быстро успокаивается из-за внутреннего трения в резине. Фактически в слишком аккуратно изготовленной машине с ничтожным трением исследуемые нами эффекты почти полностью маскируются колебаниями. Трение же в оси также маскирует их, доставляя колесу новые положения равновесия, в которых упругие силы не уравновешены.

Теперь, после проведенного выше анализа, мы можем следующим образом рассмотреть изменение положения равновесия с изменением . Пусть проходит некоторый путь в С. Тогда наблюдаемое положение равновесия пройдет путь в , лежащий над путем в С. Из-за складок поверхности этому пути, возможно, придется прыгать с одного листа поверхности на другой. Мы предполагаем, что наша (непрерывная) физическая система делает соответствующие прыжки настолько быстро, что можно пренебречь затрачиваемым на это временем. Исследование положений равновесии само по себе не может сказать нам, где будут происходить прыжки, так как в принципе они возможны в любой точке , над которой лежит два или больше положений равновесия. Необходимая дополнительная информация содержится в деталях динамики. Однако вместо того чтобы призывать на помощь динамику, мы примем следующее соглашение, которое находится в неплохом соответствии с фактами и которое Том называет принципом (максимального) промедления: система делает прыжок лишь тогда, когда у нее не остается другого выбора. Это означает, что путь, проходимый положением равновесия, сменяет лист на поверхности, лишь когда он проходит через складку, и лист, на котором он находился, исчезает. Для быстрых изменений управляющих параметров этот принцип нарушается.

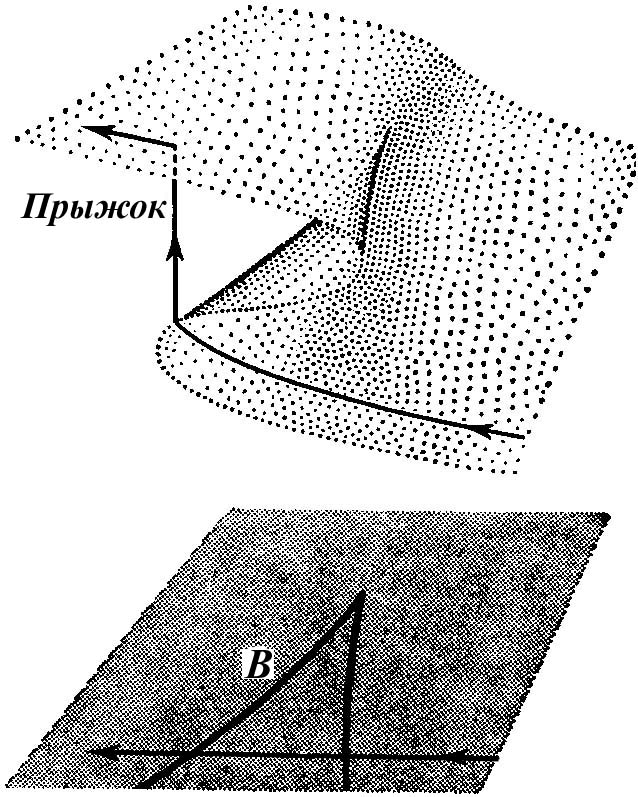
Рисунок 1.30 - Работа машины Зимана, когнда путь входит в область с снизу слева и выходит из нее снизу справа

Поскольку проведенный нами анализ относится к положениям равновесия вблизи точки , мы можем ответить на заданный ранее вопрос, для случая, когда путь входит в область с снизу слева и выходит из нее снизу справа. Такой путь в С вместе с соответствующим путем положения равновесия, получаемым по принципу промедления, показан на рисунке. Из него видно, что прыжок происходит, когда путь покидает область, но не когда он в нее входит. Последовательность графиков для функций энергии и соответствующие критические точки показаны на рисунке: прыжок происходит, когда минимум и максимум сливаются и уничтожают друг друга.

Рисунок 1.31 - Возможные критические точки для машины Зимана

Прыжки являются примерами того, что Том и Зиман называют катастрофическими прыжками (скачками). Ниже мы будем называть и переменными управления (или управляющими переменными, или управляющими параметрами), a – переменной поведения (или переменной состояния, или поведенческой переменной).

При помощи катастрофы сборки Уитни объясняются, следующие явления, которые экспериментально проверяются на машине.

Первое явление – катастрофические прыжки происходят тогда, когда гладкие изменения в управлении вызывают разрывные изменения состояния.

Второе явление – гистерезис (название взято по аналогии с подобным явлением в магнетизме, которое, по всей видимости, может быть подведено под рассматриваемую теорию). Если мы обратим путь в плоскости параметров, это не обязательно приведет к обращению пути в пространстве состояний. Это продемонстрировано на рисунке а. Принцип промедления снова показывает, что прыжок происходит при прохождении бифуркационного множества, но так как мы теперь путешествуем в обратную сторону, это произойдет на другой стороне области.

Третье явление – расхождение: небольшие различия в пути могут повлечь за собой (без всяких скачков) большие различия в состоянии, даже если пути начинаются и кончаются в одних и тех же точках (рисунке 1.31 б).

Четвертое заключается в том, что из одного состояния в другое можно перейти или гладко, или со скачком, в зависимости от пути (рисунке 1.31 в). Можно было бы отметить и многие другие явления. Мы будем дальше исследовать их по мере необходимости. Читателю стоит проверить, что отмеченные четыре явления действительно имеют место в нашей машине.

Используя принцип промедления, читатель может теперь с помощью этой поверхности предсказать поведение машины для любых путей, которые различными способами обходят клювы, и притом без всякого труда; сомнительно, смог ли бы он это сделать, не имея перед собой рисунок.

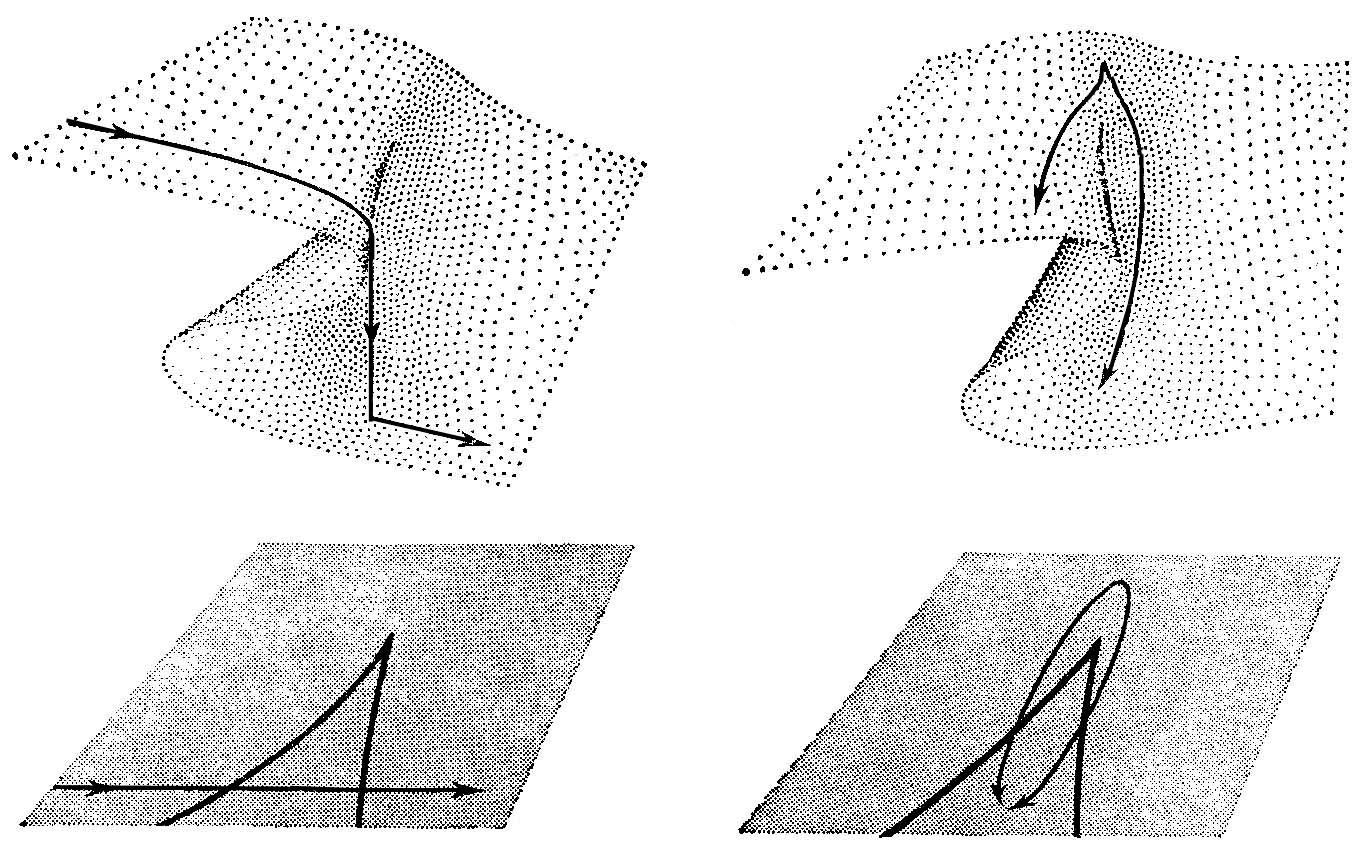
а б

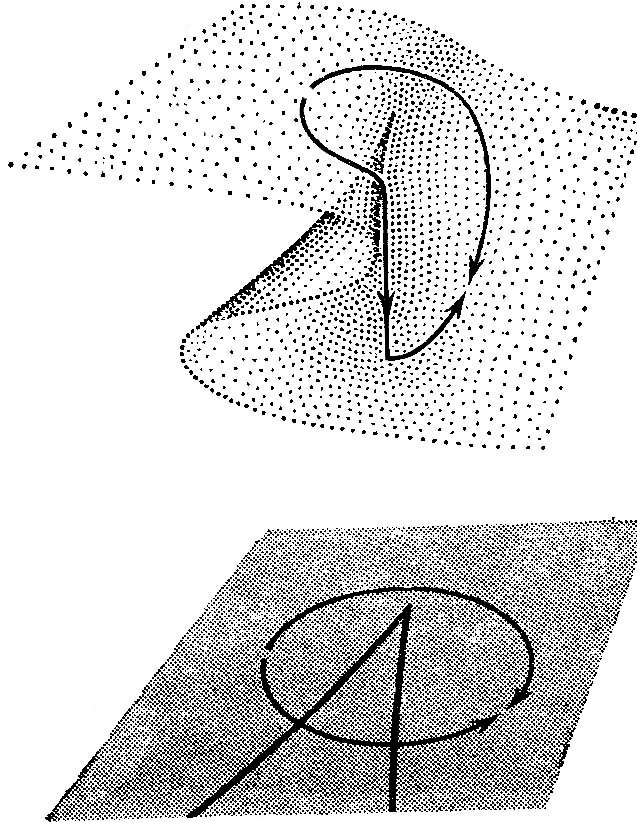
в

Рисунок 1.31 - При помощи катастрофы сборки объясняются, следующие явления: а – гистерезис; б – расхождение;

в – возможность различных путей (со качком и без него)

Структурная устойчивость семейств

В некотором отношении более поучительно рассмотреть пример неустойчивости, так как всегда легче увидеть неполадки, а затем можно сказать, что «устойчивость – это когда такое не случается».

Если бы, скажем, мы провели исследование машины Зимана лишь для управляющих точек на оси , то мы пришли бы к семейству функций

.

Критические точки находятся здесь из уравнения

,

они лежат на прямой и параболе , как это показано на рисунке а. Эта диаграмма часто встречается в книгах по теории бифуркаций. Для многих целей это описание может оказаться вполне адекватным. Однако оно не является структурно устойчивым и не позволяет охватить все моменты поведения машины. Например, на рисунке а при использовании принципа промедления мы не получим никаких катастрофических скачков.

Действительно, возмутим семейство приведенных функций малым членом , что дает

.

Теперь критические точки находятся из уравнения , и соответствующий график (для малых ненулевых ) выглядит примерно так, как показано на рисунке б. Топология этого графика совсем другая. Например, он несвязен и не имеет точек самопересечения. Это верно для сколь угодно малых .

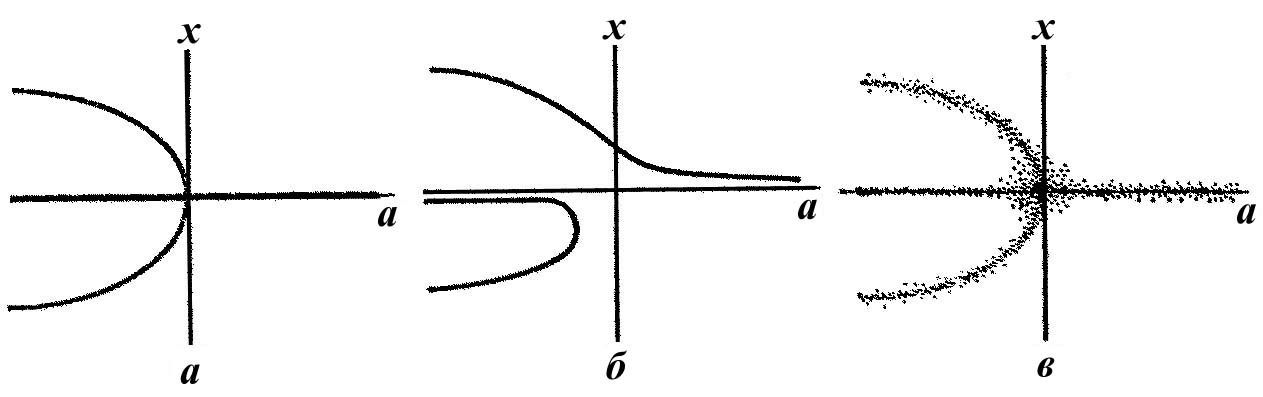
Рисунок 1.32 - Структурная устойчивость семейств:

а – семейство кананических точек;

б – семейство канонических точек с учетом малых возмущених;

в – эксперимент

Имеет это значение или нет, зависит, конечно, от точной постановки вопроса, на который ищется ответ. Рисунок б служит хорошим приближением к рисунку а в других, нетопологических смыслах. Например, оба они очень похожи на рисунке в, который может принадлежать как раз к тому типу, который желают получить в эксперименте!

Дело, однако, в том, что мы не можем пренебречь структурной неустойчивостью с самого начала; прежде чем убедиться в ее безвредности, нужно проанализировать ее влияние на интересующие нас свойства. Например, от структурной неустойчивости функции , нельзя избавиться при помощи диаграммы вроде той, что показана на рисунке.

С другой стороны, полное семейство катастрофы сборки

является структурно устойчивым. В его правдоподобии можно убедиться при помощи следующего очень грубого рассуждения:

- возмущения порядка выше четвертого не должны оказывать никакого качественного влияния;

- члены четвертого порядка, квадратичные и линейные и так учитываются;

- кубические члены можно устранить подходящей заменой координат, как это делалось при анализе машины Зимана;

- наконец, постоянные не влияют на критические точки.

Сделать это рассуждение чем-то большим, чем благое пожелание, вероятно, невозможно, так как оно не учитывает всех имеющихся здесь трудностей; строгое доказательство совсем другое и лежит глубже.

Из структурной устойчивости катастрофы сборки следует, в частности, что малые погрешности при построении машины Зимана не должны заметно влиять на ее поведение. Эксперимент показывает, что даже очень большие погрешности могут не приводить ни к чему плохому. Иногда локальное менее локально, чем это ожидают.