3.5 Отказы отдельных элементов оборудования

Интенсивные механические деформации деталей оборудования, подверженного динамическим нагрузкам, приводят к следующим отказам:

- поломки деталей из-за интенсивных нагрузок, превышающих несущую способность;

- накопление повреждений в материале отдельных деталей, приводящее к разрушению. Особенно при действии знакопеременных нагрузок;

- пластические или недопустимые и необратимые изменения в деталях, препятствующие функционированию аппаратуры;

- интенсивный рост технологических дефектов в конструкциях и оборудовании, подвергавшихся сложной обработки, в частности увеличение трещиноватости материала и т. д.

Отказы, когда нагрузка превышает прочность детали

Проследить воздействие механической нагрузки на отказ в сложных современных машинах не представляется возможным, особенно если это касается оборудования, где отказы наблюдаются и в стационарных условиях. Мы не можем, например, в данный момент времени точно сказать, какая доля отказов в машине связана с наличием трещин в материале, раковин в спайке и сварке материалов. Эти дефекты в определенной мере влияют на долговечность и надежность. Изучение их даже независимо от других факторов, влияющих на надежность, помогает проектировщикам выбрать наиболее эффективные пути ее повышения.

Даже тщательно изготовленные образцы элементов конструкций значительно отличаются по своим прочностным качествам, не говоря уже о сложных конструкциях и реальных технологиях. При расчетах надежности необходимо учитывать статистический характер свойств реальных объектов.

Разброс прочностных параметров инженерных конструкций обычно вызывается большим количеством случайных факторов:

• неоднородностью материала,

• нестабильностью технологии изготовления,

• нестабильность условий эксплуатации и т. д.

Поэтому можно считать, что распределение предела прочности конструкций достаточно хорошо описывается нормальным законом. Реальные конструкции под действием достаточно интенсивного и частого потока воздействий приходят в колебательное движение.

Воздействия на конструкцию часто носят характер случайного непрерывного процесса, вызывающие соответственно непрерывные деформации изделий. В этом случае для анализа надежности используется теория случайных выбросов.

Назначается некоторый допустимый уровень для изменения параметров конструкции во времени (например, напряжения или деформации), фиксируется момент времени, когда выбранные параметры достигают этого критического уровня и считают его за момент отказа. Надежность конструкции, как вероятность нахождения выбранных параметров в допустимых интервалах, выражается хорошо знакомой нам формулой , где – интенсивность потока случайных выбросов.

В случае нормального одномерного стационарного процесса

,

где – допустимое значение для абсолютного значения случайной функции ; – среднеквадратичное отклонение этого процесса; – среднеквадратичное отклонение производной случайного процесса, т. е. функции .

Отказы в результате накопления повреждений в материале

Известно, что длительное воздействие переменных нагрузок меняет внутреннюю структуру материала конструкции даже при напряжениях, меньших предела упругости. Такое разрушение деталей оборудования можно классифицировать как усталостное.

Наука об усталости материалов в основном базируется на экспериментальных данных. Для образцов из определенного материала или для детали в целом строят так называемую диаграмму Велера, на которой указывают число циклов нагружения до разрушения при соответствующей амплитуде напряжения, вызванного нагрузкой. Стендовые вибрационные испытания деталей машин и аппаратов химических производств подтверждают возможность этого подхода (рисунок 4.18).

Метод Велела можно легко обобщить на случай, когда механические параметры изделия испытывают всевозможные флюктуации из-за неоднородности материала, случайных отклонений технологического процесса и т.д.

В этом случае мы будем иметь вместо одной кривой семейство. У каждой кривой должна быть указана доля не разрушающихся конструкций при данном напряжении и числе циклов .

Рисунок 4.18 – Диаграмма Велела для деталей оборудования

Дальнейшее обобщение метода Велера для случайной нагрузки уже не столь просто и однозначно. Основная трудность заключается в том, что для этого метода фундаментальное значение имеет понятие цикла, который теряет точный смысл, например для случайного непрерывного процесса.

Необходимо найти подходящее определение цикла в случайном процессе и рассматривать его как последовательность таких условных циклов.

Циклом случайного параметра в материале будем называть событие, состоящее в том, что параметр , непрерывно нарастая от некоторого значения (минимума), достигает некоторого максимума и убывает далее вновь до некоторого минимального значения, как показано на рисунке.

Рисунок 1.19 – Случайный цикл нагружения

Рассмотрим приложение этого определения к расчету долговечности детали, если мерой накопленных повреждений является величина

,

где – число циклов нагрузки, амплитуда которых имеет максимум в пределах от , до ; – предел усталости данной детали.

Параметр может принимать следующие значения в зависимости от конкретных свойств и параметров деформируемого предмета (детали). Для деталей химической аппаратуры предварительные испытания элементов на вибростендах позволяют выбрать значение из интервала .

Предполагается, что разрушение происходит, как только сумма достигнет некоторого критического значения . Для некоторых металлов, используемых в машиностроении, эти критические значения ( где – модуль Юнга) следующие:

Материал
Сталь малоуглеродистая	2,5 105
Сталь (45 %С)	3,5 105
Сталь пружинная	6,0 105 - 8,0 105
Алюминий	0,8 105
Медь	1,4 105

В формуле , является фиксированной величиной, обозначающей уровень, за которым происходит случайный выброс, формирующий условный цикл. Случайными величинами являются , т. е. число выбросов случайного процесса за уровень . Поэтому величина является случайной, и для определения долговечности необходимо перейти к статистическим характеристикам.

Отказы при достижении пластических (необратимых) деформаций

В последнее время наука о пластических деформациях силовых элементов конструкций развивалась в связи с технической необходимостью оптимально использовать несущую способность изделий. Однако для деталей оборудования значительные деформации недопустимы, поскольку форма конструкции самым существенным образом влияет на качество функционирования машины в целом.

Имеющиеся подходы оценки надежности при достижении пластических деформаций относятся к мелкомасштабным деталям или при работе машины в условиях высоких температурах, когда могут проявляться пластичные свойства материала.

Отказы при наличии трещин и дефектов в материале конструкции

Большинство материалов деталей современных машин и аппаратов претерпевает значительные воздействия при технологической обработке и изготовлении. Как в самой толщине материала, так и в зонах сварки, спайки образуются раковины, трещины и другие дефекты, которые при воздействии механических эксплуатационных нагрузок начинают расти, и приводят к сокращению срока службы и надежности машин.

Основным показателем технологической дефектности деталей химической аппаратуры является неоднородность интенсивности отказов во времени при испытании достаточно представительной партии (рисунок 1.20).

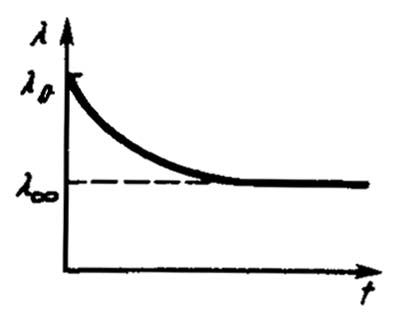
Рисунок 1.20 – Интенсивность отказов во времени при вибрациях

Существование на начальном этапе стендовых вибрационных испытаний сравнительно высокой интенсивности отказов свидетельствует о наличии скрытых дефектов у некоторой части изделий, которые вызывают их относительно быстрый выход из строя.

Одним из типов дефектов, достаточно тщательно изученным в современной литературе по механике, является трещина. В работах по теории упругости показано, что равномерное напряжение растяжения в материале пластины вызывает при вершине трещины концентрацию напряжения (рисунок 1.21).

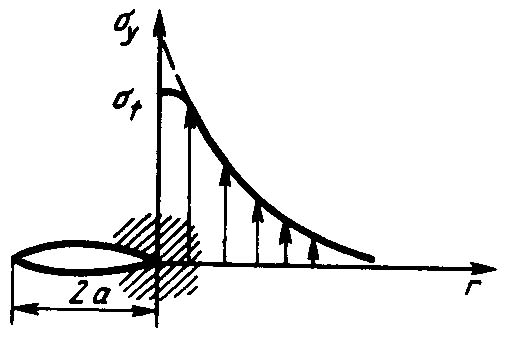
Рисунок 1.21 – Концентрация напряжений у вершины трещины в материале (пунктирная линия соответствует расчету по теории упругости)

Такое поле напряжений имеет особенность в вершине трещины и реально существовать не может. Вокруг вершины трещины образуется зона пластических деформаций, которая приводит к тому, что около самой вершины образуется область размером , где напряжения устанавливаются приблизительно возле предела текучести материала .

На рисунке эта зона заштрихована, а фактическая эпюра напряжения изображена пунктиром.

Компоненты тензора напряжений можно записаны в виде:

,

где введена константа (коэффициент интенсивности напряжений). Это единственная величина, которая характеризует напряженное состояние, так как функции неизменны при изменении условий нагружения. Именно эта величина , как подтверждают эксперименты, может быть выбрана в качестве оценки прочности материала с трещиной.

При достижении определенного критического значения (безразлично за счет внешней нагрузки или размера ) величины коэффициента интенсивности напряжений , т. е. при больше , трещина становится неустойчивой и растет.

Это критическое значение называется вязкостью разрушения материала и является мерой оценки трещиноватости и трещиностойкости материала. В таблице представлены параметры материала, влияющие на рост отдельных трещин и на несущую способность всей детали, технология изготовления которой сопряжена с появлением каких-то характерных микродефектов.

Материал	Временное сопротивление разрыва , дан/мм2	Предел текучести , дан/мм2	Вязкость разрушения , дан/мм3/2
Сталь	185	150	150
Легированная сталь	188	177	290
Алюминий	57	51(сплав)	104

Вероятность безотказной работы по заданному критерию

Работоспособность деталей машин характеризуется рядом критериев: прочностью, износостойкостью, жесткостью, теплостойкостью, виброустойчивостью, точностью.

Расчет сводится к сопоставлению по отдельным критериям расчетных параметров с их предельными величинами:

- характеристиками прочности (пределом прочности, текучести, выносливости),

- предельной нагрузкой,

- ресурсом,

- предельными перемещениями (упругими, вызванными износом, температурными),

- теплостойкостью масла и материалов,

- предельными частотами и амплитудами колебаний,

-динамической устойчивостью.

Предельные величины расчетных параметров критерия выбирают по нормативным или справочным данным или устанавливают путем испытаний или наблюдений в эксплуатации.

Работоспособность деталей по заданному критерию обеспечена, если расчетный параметр критерия меньше его предельного значения . В общем случае параметр не должен выходить за предельное значение.

В настоящее время основное применение имеет расчет с помощью заранее задаваемых коэффициентов безопасности , соответственно расчетное условие . Величины рассматривают детерминированными, хотя в действительности они могут иметь большой случайный разброс . Расчет приходится вести по наиболее неблагоприятным значениям, когда истинное значение коэффициента безопасности остается неизвестным.

С переходом на вероятностные методы расчета и рассматривают как случайные величины, и мерилом надежности является вероятность безотказной работы по заданному критерию. Расчетное условие для обеспечения вероятности безотказной работы в 50% случаев имеет вид , а для обеспечения вероятности

,

где – средние значения величин и ; – среднее квадратичное отклонение разности двух случайных величин и ; – среднее квадратичное отклонение величины и ; – квантиль нормированного нормального распределения – функция от вероятности .

Здесь, полагают, что разность , распределена по нормальному закону, хотя строго это положение выполняется только при нормальных распределениях и ,

Вероятность безотказной работы определяется по заданному критерию в зависимости от величины квантили:

.

Представляет существенный интерес связь квантили , как характеристикой вероятностного расчета, и коэффициентом безопасности , рассчитанным по средним значениям. Соответственно разделим числитель и знаменатель дроби на и введем коэффициенты вариации и , тогда

.

Зависимость для параметра может быть представлена следующим образом: , где – случайные факторы. Форма представления зависимости для параметра полностью применима для параметра .