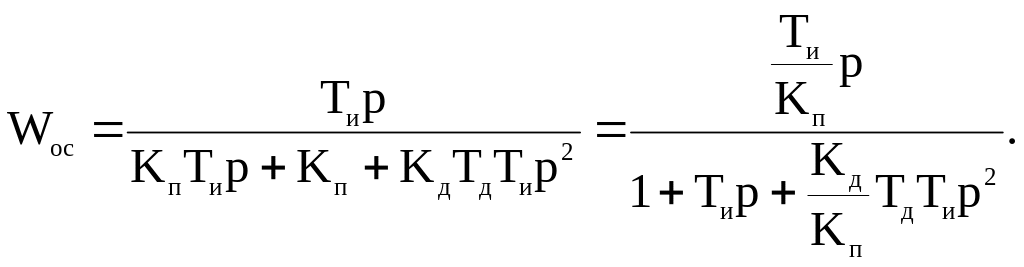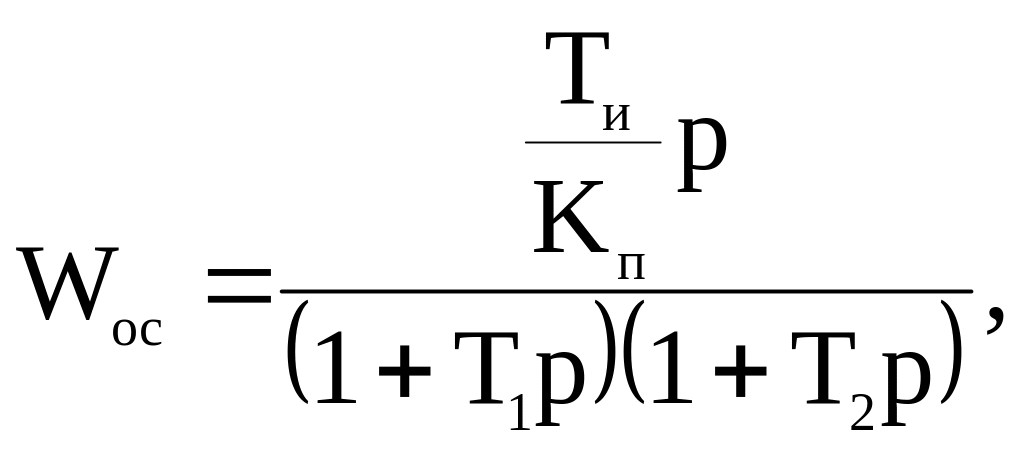- •Введение
- •Объекты регулирования и их характеристики
- •Методы определения свойств объекта
- •Подставляя относительные величины
- •Умножим и разделим члены левой части уравнения на заданное значение температуры Θн, и все уравнение разделим на номинальное значение теплоты qхн.
- •Выходная величина теплообменника в операторной форме
- •Величина под касательной вс равна сумме постоянных времени
- •Отсюда,
- •Выбор регулятора
- •Интегральный, или и - закон регулирования. Он описывается уравнением
- •Оптимальная настройка регуляторов
- •Настройка регуляторов, выполненных на основе микропроцессорных
- •Влияние запаздывания в системе на качество регулирования
- •Микропроцессорные контроллеры для систем автоматизации
- •Нумерация переменных в микроле
Выбор регулятора
4.1. Выбор типа регулирования
Тип регулирования выбирается с учетом свойств объекта и заданных параметров переходного процесса. К параметрам переходного процесса могут предъявляться различные требования. В одних случаях оптимальным является процесс с минимальным значением динамической ошибки, в других - с минимальным значением времени регулирования и т.д. Обычно выбирают один из трех типовых переходных процессов: граничный апериодический, с 20% перерегулированием, с минимальной квадратичной площадью отклонения.
Граничный апериодический процесс характеризуется отсутствием перерегулирования, минимальным общим временем регулирования и наименьшим воздействием регулятора на объект (что вызывает наибольшее отклонение регулируемой величины от заданного значения). Такой переходный процесс используется в качестве оптимального при значительном влиянии регулирующего воздействия на другие технологические величины объекта, чтобы свести их отклонение к минимуму.
Процесс с 20% перерегулированием характерен большей величиной воздействия регулятора и меньшим отклонением, при этом время регулирования несколько возрастает. Этот процесс выбирают в качестве оптимального, когда допустимо небольшое перерегулирование.
Процесс с минимальной квадратичной площадью отклонения обладает значительным перерегулированием (до 40%), большим временем регулирования и наименьшей величиной динамической ошибки.
Ориентировочно характер действия регулятора определяется по отношению запаздывания τ к постоянной времени объекта Т.
При
![]() выбирается позиционное регулирование.
выбирается позиционное регулирование.
При
![]() выбирается непрерывное регулирование,
либо импульсное.
выбирается непрерывное регулирование,
либо импульсное.
При
![]() применяют многоконтурные системы
регулирования и принимают
меры по компенсации влияния запаздывания.
применяют многоконтурные системы
регулирования и принимают
меры по компенсации влияния запаздывания.
Более подробно вопрос выбора типа регулятора рассмотрен в [21], где приведены необходимые алгоритмы и таблицы.
4.2. Выбор закона регулирования
В зависимости от типа уравнения связывающего величину отклонения регулирующей величины ε(t) и перемещение регулирующего органа Y(t) различают следующие законы регулирования.
Интегральный, или и - закон регулирования. Он описывается уравнением
|
(55) |
где Ки – коэффициент пропорциональности, численно равный скорости перемещения регулирующего органа на единицу измерения регулируемой величины.
Передаточная функция И – регулятора
|
(56) |
Регуляторы, у которых регулирующее воздействие пропорционально интегралу отклонения регулируемого параметра, называют астатическими. И - регуляторы могут устойчиво регулировать работу лишь объектов с самовыравниванием.
Пропорциональный, или П - закон регулирования. Описывается уравнением
|
(57) |
где Кп - коэффициент усиления регулятора, равен перемещению регулятора при отклонении регулируемой величины на единицу измерения.
Передаточная функция П – регулятора
|
(58) |
П - регуляторы называют статическими. Они могут устойчиво регулировать работу практически всех объектов. Их отличает простота реализации. Однако они обладают статической ошибкой, величина которой зависит от нагрузки объекта.
Пропорционально - интегральный, или ПИ - закон регулирования описывается уравнением:
|
(59) |
где Ти – время изодрома.
Регулирующее воздействие пропорционально отклонению и интегралу отклонения регулируемой величины.
Передаточная функция ПИ – регулятора
|
(60) |
ПИ – регулятор называют изодромным. ПИ - регуляторы отличаются простотой конструкции, позволяют устойчиво и без статической ошибки регулировать работу большинства промышленных объектов, вследствие чего получили наибольшее применение в практике.
Пропорционально - интегральный закон с введением производной, или ПИД - закон регулирования. Описывается уравнением:
|
(61) |
где Тд – время предварения.
Передаточная функция
|
(62) |
ПИД регуляторы называют регуляторами с предварением.
Введение в закон регулирования производной позволяет повысить устойчивость системы регулирования, уменьшить время регулирования, улучшить другие ее качественные показатели.
4.3. Реализация законов регулирования
Сформировать необходимый закон регулирования можно двумя способами. Первый способ состоит в том, что необходимая передаточная функция получается в результате суммирования передаточных функций усилительных, интегрирующих и дифференцирующих звеньев. При втором способе необходимая передаточная функция получается охватом звеньев регулятора звеном обратной связи с определенной передаточной функцией. Рассмотрим эти способы на примере реализации ПИД - закона регулирования.
Из выражения для передаточной функции для ПИД - закона (62) следует, что ее можно получить как сумму передаточных функций трех звеньев: усилительного, интегрирующего и дифференцирующего (рис.16).
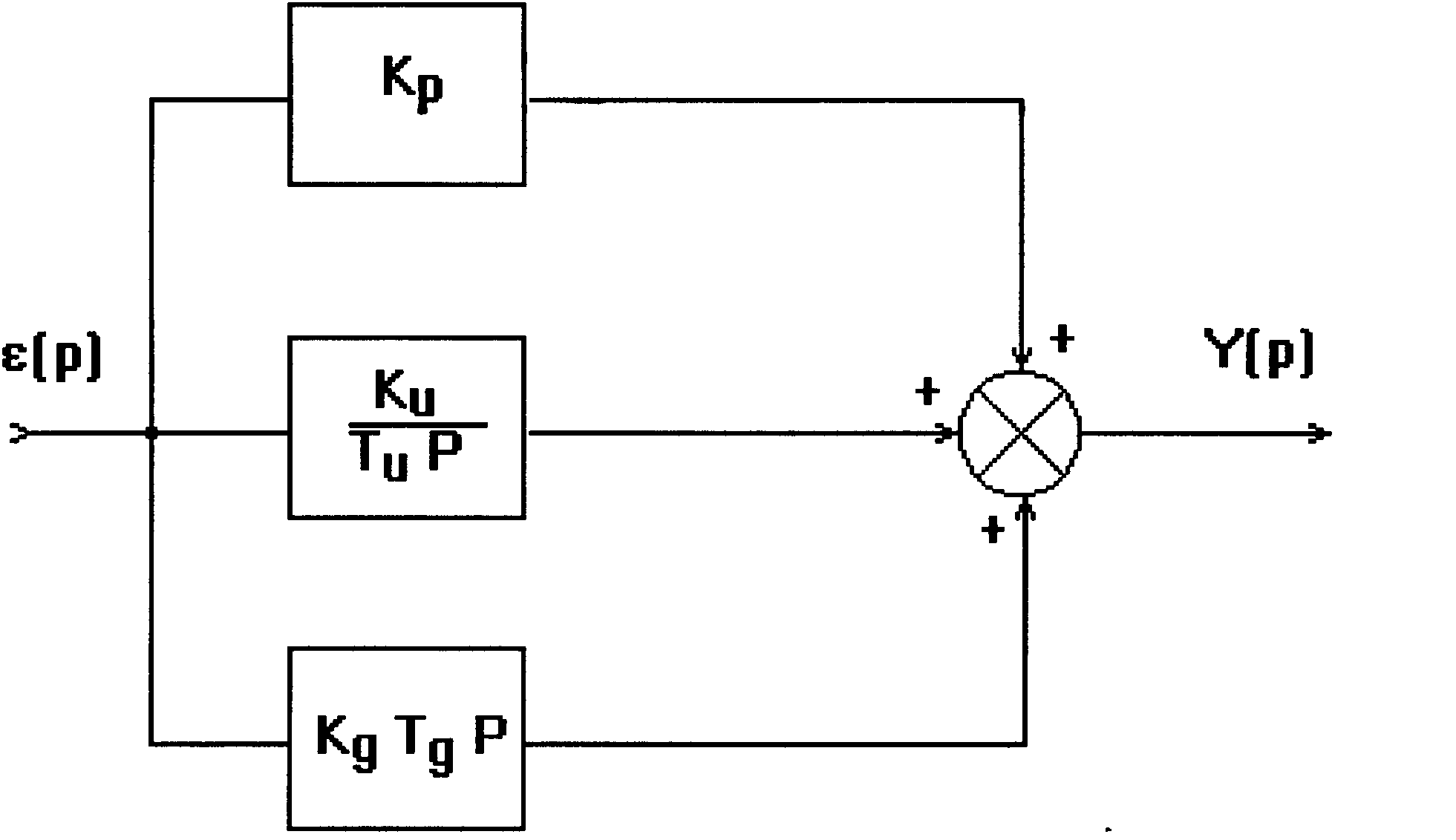
Рис.16
При реализации других законов регулирования (П, ПИ, И) нужно использовать соответствующие комбинации звеньев.
Основными элементами регулятора, с помощью которых формируется закон регулирования, являются измерительные устройств усилители, исполнительные механизмы и звенья обратной связи.
Допустим регулятор состоит из усилителя и сервомотора.
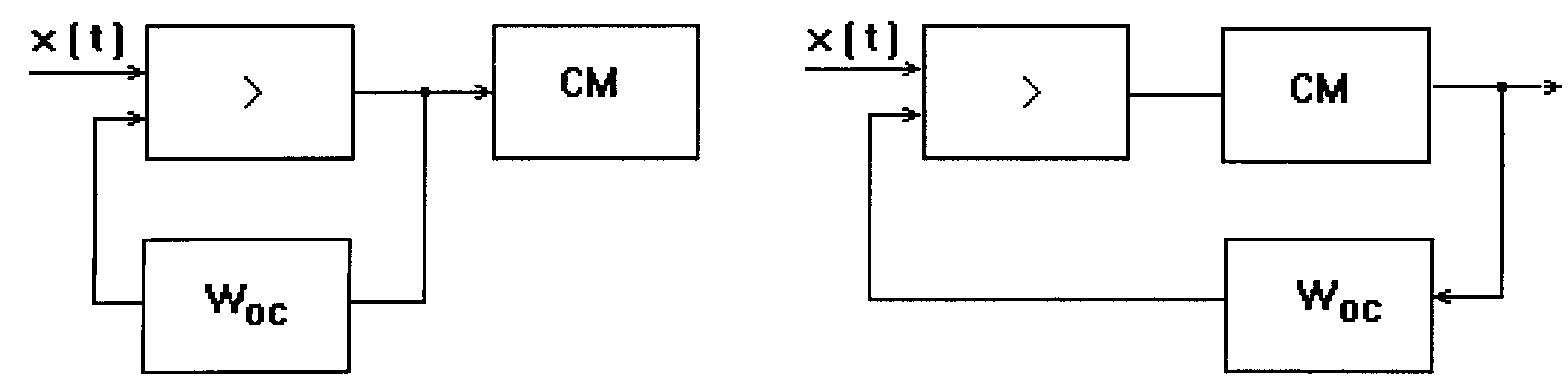
Рис.17
Усилитель - безынерционное звено с передаточной функцией Wy = К. Сервомотор - интегрирующее звено с передаточной функцией Wcm = 1/(Тср), где Тс - время перестановки регулирующего органа из одного крайнего положения в другое. Чтобы реализовать ПИД - закон регулирования, включим обратную связь. Рассмотрим два способа: обратной связью охвачен усилитель (рис.17, а) и обратной связью охвачены усилитель и сервомотор (рис. 17, б).
Как известно, передаточная функция
звена, охваченного обратной связью,
при К >> 1 равна
![]() .
Поэтому, в первом случае передаточная
функция регулятора
.
Поэтому, в первом случае передаточная
функция регулятора
|
(63) |
Для ПИД закона:
. |
(64) |
Отсюда
|
(64) |
Таким
образом, в обратную связь нужно включить
колебательное звено с коэффициентом
усиления
![]() ,
временем изодрома Ти и временем
предварения
,
временем изодрома Ти и временем
предварения
![]() .
.
Во втором случае:
|
|
Это выражение можно привести к следующему:
|
(65) |
где
![]() ,
,
![]() .
.
Т.е. в обратную связь нужно включить последовательно соединенные апериодическое и реальное дифференцирующее звенья.
Таким же образом можно сформировать и любые другие законы регулирования.
При использовании промышленных регуляторов на основе микропроцессорной техники (Ремиконт, Ломиконт и др.) необходимый закон регулирования устанавливается программно.

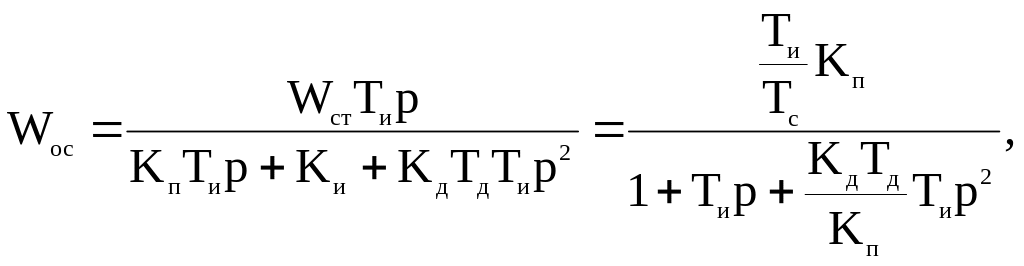 или
или