4.4 Пример выполнения кинематического исследования механизма

4.4.1.Исходные данные: схема механизма, рис. 8а; длины звеньев; расстояния l₁, l₂, l₃, определяющие взаимное положение точек О₁,О₂,О₃.;

Рис.8

частота и направление вращения кривошипа n об/мин ; положение центров масс «s» звеньев.

4.4.2. Построение планов механизма

Выбираем масштаб длин для плана механизма по формуле:

μ_l = l₁/O₁0₂ (м/мм)

l₁ – истинная длина кривошипа в метрах; О₁А – длина кривошипа на чертеже в миллиметрах.

В соответствии с масштабом μ_l определяем на чертеже все линейные размеры. Для этого длину каждой линейной величины делим на μ_l.

Наносим точки О₁, О₂ и О₃.

Анализ схемы механизма показывает, что кулиса 3, вращаясь на шарнире О₂, должна проходить через т. А во всех её положениях. Когда она расположится по касательной к траектории т. А, механизм займёт одно из двух крайних положений. Следовательно, из точки О₂ проводится касательная к окружности радиуса АО₁, Эта прямая определит крайнее положение звена 3, а в точке касания этой прямой с окружностью – точке А₀ механизм займёт одно из двух крайних положений.

Точка В лежит на расстоянии ВО₂ от точки О₂. Это позволяет найти её крайнее положение – В₀. Далее радиусом ВС проводится засечка на дуге, описанной из центра О₃ радиусом СО₃. Пересечение дуги и засечки определит крайнее положение С₀ точки С.

Соединив соответствующим образом полученные точки, получим план механизма в исходном «нулевом» положении.

Строим например 8 равноотстоящих друг от друга положений ведущего звена 1, причём, за начальное принимаем крайнее положение «0». Для этого окружность т. А, начиная с т. А_о., делим на 8 равных частей. Нумеруются положения в направлении вращения ведущего звена. Затем полученные т.т. А_i соединяются с т. О₁.

Положение остальных звеньев определяется способом засечек, что уже было показано при построении крайнего положения механизма.

Траектория заданной точки строится путём соединения плавной кривой промежуточных её положений. На рисунке 8а показана траектория т. С.

4.4.3. Построение плана скоростей

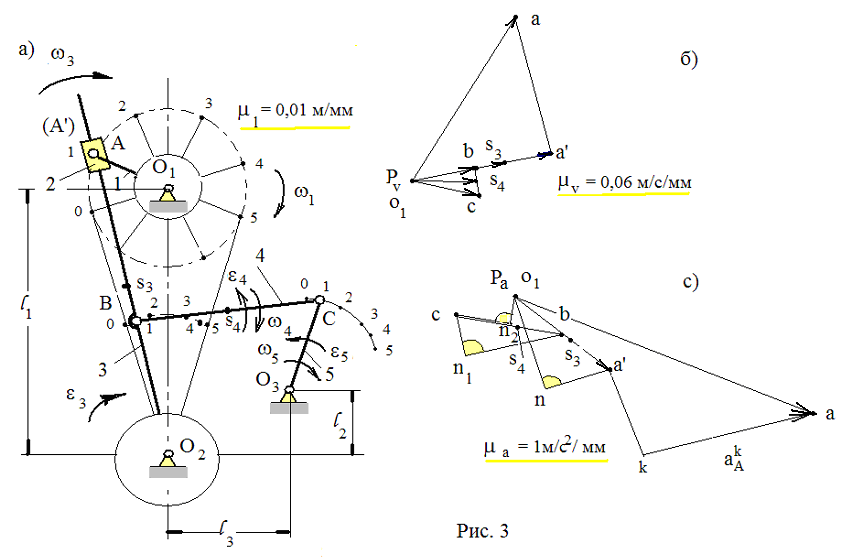
Построение плана выполним для положения «1», вычерченного контурной линией, рис. 8б.

Зная скорость кривошипа, можно найти скорость его конца А по формуле:

V_a =ω₁ l₁ = π l₁n/30;

Где

V_a – скорость т. А, направленная перпендикулярно кривошипу в сторону его вращения,

n об/мин – частота вращения кривошипа,

ω₁ сек^-1 – угловая скорость кривошипа.

Из произвольной т. P_v – полюса плана скоростей проводим вектор (P_{v a}) , представляющий вектор V_a в определённом масштабе μ_v, величина которого равна

μ_v = V_a/P_va (м/сек)/мм

Для определения абсолютной скорости т. А’ звена 3, направление которой перпендикулярно этому звену, (точки А и А’ совпали на чертеже, но не в механизме) пользуемся теоремой сложения скоростей в сложном движении:

Va’ = Va + Va’a (1)

Э то читается так:

«Скорость т. А’ равна геометрической сумме скоростей т.А и скорости т. А’ относительно т. А».

Величина скорости Va’a неизвестна, а направление её – вдоль звена 3 т.к. как относительное движение происходит вдоль кулисы.

В дальнейшем вектор, известный по величине и направлению в векторных уравнениях подчёркиваем двумя чертами, а вектор, известный только по направлению – одной чертой, см. (1).

Из точки «а» плана скоростей, рис. 8б, проводится параллель АВ, а из полюса Pv – прямая перпендикулярная АВ. В их пересечении получаем т. «а’». Соединив последнюю с полюсом P_v, получим вектор P_va’, изображающий скорость Va’.

Вектор aa’ изображает относительную скорость Va’a. Стрелка на отрезке aa’ определяется первой буквой индекса у вектора относительной скорости Va’a. В данном случае стрелка ставится в т.a’ на плане скоростей. Это правило назовём правилом индексов.

Точки О₁, О₂ и О₃ механизма неподвижны и на плане скоростей совпадают с полюсом Р_v

Скорость т. В определится по теореме о подобии, согласно которой

О₂А’/О₂В = P_va’/P_vb

Откуда отрезок на плане скоростей

P_vb = О₂В х P_va’/ О₂А’

Здесь отрезки О₂В и О₂А’ замерены на плане механизма.

Найденный вектор P_vb изображает абсолютную скорость V_B.

Теперь можно по теореме о сложении скоростей найти скорость т. С

V_c = V_B + V_CB

Подчёркнутые одной чертой векторы направлены перпендикулярно звеньям соответственно №5 и №4. Поэтому на плане скоростей поступаем так: из т. b проводится перпендикуляр к ВС, а из полюса P_v – перпендикуляр к СО₃. В пересечении получаем т.c. Тогда отрезок P_vc представит абсолютную скорость Vc, а отрезок bc – относительную скорость V_CB (по правилу индексов у него стрелка в букве с).

Скорости центров масс s на плане скоростей находятся по теореме подобия. Так на плане скоростей т. S₄ делит пополам отрезок bc так же как и на плане механизма она делит звено ВС. Соединив т. S₄ с полюсом, получим вектор P_v s₄ эквивалентный скорости V_s4.

Аналогично строятся планы скоростей для других положений механизма.

Имея планы скоростей, можно определить численные значения абсолютных и относительных скоростей точек для каждого положения механизма. Для этого величину соответствующего отрезка на плане скоростей умножаем на коэффициент μ_v его масштаба. На пример скорость т. В, рис 8а и 8b

V_B = (P_v b) _x μ_v (м/с)

Скорость движения т. С относительно т. В (стрелка в т. «С»), рис.8b,

V_cb = (bc) x μ_v

В последних выражениях выделенные скобками отрезки замеряем на плане скоростей в «мм».

Теперь можно перейти к определению угловых скоростей звеньев. Для первого звена с известной частотой вращения n₁ об/мин она определится по формуле

ω₁ =π n₁/30 (сек^-1)

Угловая скорость звена 3:

ω₃ = V_B/l₃

Здесь длина l₃ звена 3 – в метрах.

Перенося мысленно вектор V_B в точку В механизма, определим направление вращения звена 3 – по часовой стрелке.

Угловые скорости звеньев 2 и 3 – одинаковы, т.к. оба звена составляют поступательную пару с общим переносным вращательным движением.

Для звена 4 угловая скорость определяется по относительной V_CB, а для звена 5 – по абсолютной Vc:

ω₄ = V_CB /l_CB ω₅ = Vc/l_CO3

Для остальных положений механизма угловые скорости определяются аналогично.