4.7.3 Силовой расчет группы 4-5

Строим план группы в выбранном масштабе μ_ℓ (рис. 10а). Группа нагружается приложенными к ней силами P, G₅ ,G₄, равнодействующей Р_и4’ сил инерции звена 4.

Отброшенные связи заменяем реакциями. В точке O₃ на звено 5 действует реакция со стороны стойки Р₀₅, в точке В – реакция звена 3 на звено 4, сила P₃₄. Эти реакции неизвестны по величине и направлению. Разложим каждую из них на две составляющие (в точке 0₃ – Pⁿ_O5 по звену О₃С и P^τ_O5 перпендикулярно к O₃C; в точке B – Рⁿ₃₄ по звену BС и Р^τ₃₄ перпендикулярно к ВС.

Рассматривая равновесие звена 5, составляем уравнение моментов сил этого звена относительно точки C:

ΣМ_с =G₅ h₄ –P₀₅^τ O₃C =0

Откуда P₀₅^τ определится.

Длина плеч сил берется непосредственно на плане группы 4-5.

Из условия равновесия звена 4 можно записать:

ΣМ_с =Р₃₄τ ВС – Р_и4 h₂+G₄ h₃ = 0 .

Из этого уравнения определяем .

Рассмотрим равновесие группы 4-5:

Составим уравнение её равновесия :

.

Векторное уравнение сил группы составлено в соответствии с указанными выше правилами. Оно включает две неизвестные величины и , которые можно определить графически, построив многоугольник сил для группы (план сил группы 4-5, рис.10б).

Масштаб плана сил группы определяется по формуле

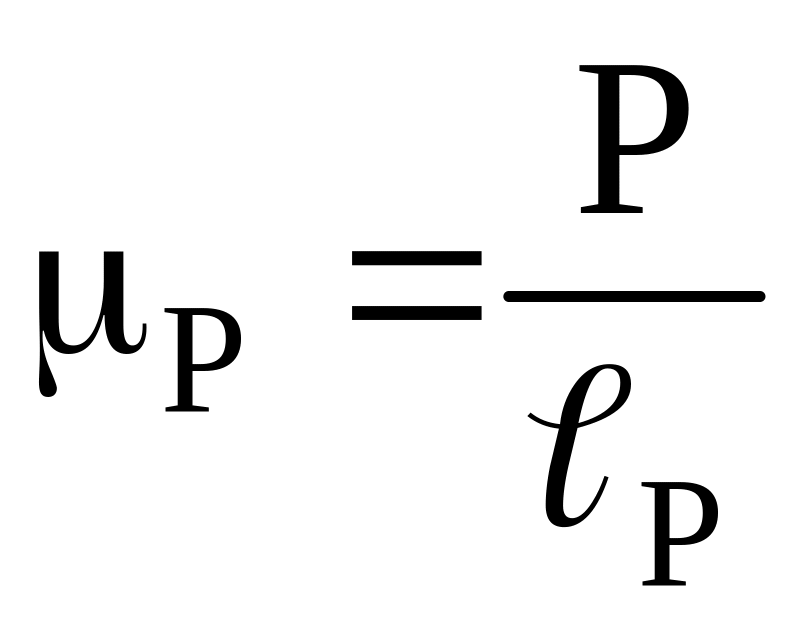
где Р – величина заданной силы в рассматриваемом положении;

ℓ_Р – длина вектора силы на плане сил группы, выбираемая произвольно.

Затем последовательно откладываются векторы сил по составленному уравнению. Искомые величины сил и определяются в результате пересечения линий действия этих сил (рис. 10б).

Реакцию в точке В, равную

можно определить на простроенном плане сил, если соединить начало вектора силы с концом вектора силы .

Реакция в точке О₃ определяется как геометрическая сумма сил

.

Для определения реакции в точке С необходимо рассмотреть равновесие звена 4 или 5. Для звена 4 получим

.

Это векторное уравнение решаем графическим построением плана сил для группы 4-5, Вектор, соединяющий конец силы с началом вектора , изображает силу Р₅₄=Р₄₅ (рис. 10б).

Заканчиваем силовой расчет группы 4-5 определением численных значений реакций , и ; для чего длину отрезка соответствующей силы на плане сил умножаем на масштаб μ_р.

4.7.4 Силовой расчет группы 2-3

Рис.11

Строим план группы в определенном масштабе длин (рис. 11a).

Группу нагружаем действующими на неё силами: силой тяжести звена 3 – G₃, приложенной в точке В, равнодействующей P_и3 cил инерции звена 3, приложенной в точке В. Отброшенные связи заменяем реакциями.

Реакция в точке O₂ стойки на звено 3 (сила ) раскладывается на две составляющие и . В точке В действует сила равная по величине, но противоположно направленная найденной силе рис. 10 б, .

В точке А действует неизвестная по величине и направлению реакция со стороны звена 1 на звено 2.

Рассмотрим равновесие звена 2. На него действует реакция со стороны звена 1 - сила и сила со стороны звена 3(считаем звено 2 не имеющим массы). Сила приложена в точке А, величина и направление её неизвестны. Сила же направлена перпендикулярно к О₂А, а величина и точка приложения её неизвестны. Из уравнения равновесия звена вытекает:

.

Следовательно, сила должна быть приложена в точке А, а направление силы , как и силы – перпендикулярно к О₂А.

Составляем уравнение моментов сил группы 2-3 относительно точки А:

,

из которого определим . При этом плечи сил замеряем в миллиметрах непосредственно на плане группы 2-3. Уравнение равновесия всех сил, действующих на группу 2-3, выглядит так:

Σрi = Р₄₃+Р_и3+G₃+Р₀₃^τ+Р₀₃ⁿ+Р₁₂ =0

Построение плана сил группы 2-3 определит величины векторов и (рис. 11б).

Для нахождения реакции на плане сил группы соединяем начало вектора и с концом вектора .

В заключение определяются численные значения реакций , Р₁₂, .

Рис.12