6. Практична частина

Практична частина роботи містить чотири окремих завдання. Завдання мають метою закрыплення практичних навичок застосування на практиці теориїі ленійного програмування, теорії прийняття рішень в умовах невизначенності та основ календарного планування.

6.1. Проектування торгівельного комплексу

У цій роботі Вам пропонується, використовуючи інструменти маржинального аналізу, теорії обмежень (TOC), лінійного програмування й теорії прийняття рішень визначити оптимальні асортименти що випускаються й реалізованих виробів, на основі техніко-економічних розрахунків по можливих альтернативах розвитку компанії ухвалити рішення щодо найбільш раціонального варіанта

Вихідна ситуація:

Керівництву виробничо-торговельного підприємства необхідно визначити оптимальні товарні асортименти для одного із залів тільки що побудованого торговельного комплексу. У залі передбачається продавати два види товарів: кухонні комбайни й міксери. Критерієм оптимальності товарних асортиментів є прибуток підприємства від його реалізації. Керівництво вирішило використовувати маржинальний аналіз для розрахунку прибутку, тому враховується тільки маржинального прибуток (прибуток без обліку постійних витрат підприємства).

Для спрощення рішення завдання ми вводимо наступні допущення:

• попит на обидва товари необмежений;

• можливості виробництва товарів мають достатній запас (див.завдання);

• розрахунок наповнення торгівельного залу провадиться для одного робочого дня;

• реалізація товарів буде відбуватися рівномірно, так, що вантажники зможуть також рівномірно наповнювати торгівельний зал;

• на початку робочого дня зал порожній.

Як обмеження Ви повинні враховувати:

1. площа торговельного залу (Ви не можете розмістити товарів більше, ніж того дозволяє торгівельний зал, для обліку можливості багаторазового використання площі протягом дня використовується коефіцієнт обіговість товарів);

2. робочий час продавців (Ви не можете продати товарів більше, ніж можуть фізично обслужити продавці);

3. можливості вантажників по доставці товарів зі складу в торгівельний зал (через торгівельний зал не може бути продано товарів більше, ніж їх туди зможуть доставити вантажники);

Відповідно до теорії обмежень (Theory Of Contractions - TOC), одного з "модних" сьогодні напрямків менеджменту, будь-яке підприємство в кожний момент часу має тільки одне обмеження - "вузьке місце" у своїй діяльності. Тому нема рації розширювати інші вузькі місця доти, поки не розширене головну, стримуючу роботу всієї системи, вузьке місце. При рішенні даного завдання Вам буде необхідно визначити поточне "вузьке місце" підприємства й оцінити ефект від його розширення.

Як інструмент рішення завдання Вам належить використовувати лінійне програмування, зокрема графічний метод рішення завдань лінійного програмування.

Вихідні дані:

	площа торгівельного залу	15 м2
	коефіцієнт обіговість товарів (середній коефіцієнт використання торгівельної площі за день)	1,33
	площа, займана кухонним комбайном	0,5 м2
	площа, займана міксером	0,05 м2
	кількість продавців у торгівельному залі ( 8-и годинний робочий день)	4 чіл
	час, затрачуваний продавцем для відпустки кухонного комбайна	0,17 години
	час, затрачуваний продавцем для відпустки міксера	0,17 години
	кількість вантажників, що доставляють товари зі складу ( 8-и годинний робочий день)	1,5 чіл (один - повниний робочий день і ще один - пів робочого дня)
	час доставки впакування кухонних комбайнів зі складу (у виробничому впакуванні)	0,5 години
	кількість кухонних комбайнів у виробничому впакуванні	5 шт
	час доставки впакування міксерів зі складу	0,3 години
	кількість міксерів у виробничому впакуванні	10 шт
	прямі витрати на виробництво кухонного комбайна	400 грн
	прямі витрати на виробництво міксера	85 грн
	торгівельна націнка на товари	25%

Завдання:

1. З т.з.максимізації маржинального прибутку підприємства визначити оптимальні асортименти торговельного залу й розрахувати значення маржинального прибутку підприємства.

2. Визначити, яке обмеження є "вузьким місцем" у діяльності підприємства, запропонувати заходу щодо усунення (розширенню) "вузького місця" і розрахувати ефект від його усунення.

Математична постановка завдання:

Позначимо товарні асортименти підприємства у вигляді невідомих змінних:

• кількість реалізованих кухонних комбайнів - x1;

• кількість реалізованих міксерів - x2.

Визначимо вид цільової функції підприємства. Оскільки метою діяльності підприємства є максимізація маржинального прибутку, що може бути визначена на основі торговельної націнки на товари, те цільова функція може бути записана в такому виді:

або

Формалізуємо обмеження, що накладаються на процес реалізації товарів:

1. По площі:

2. По продавцях:

3. По вантажниках:

4. Природно, кількість реалізованих товарів не може бути негативним:

Рішення завдання

Для того, щоб визначити область припустимих значень (ОДЗ) шуканих змінних x1 і x2, побудуємо графіки прямих, що відповідають цим обмеженням. Оскільки, як відомо, щоб побудувати графік прямій, необхідно лише дві крапки, визначимо координати цих крапок для рівняння кожного обмеження. Для цього в рівняннях замінимо знаки нерівностей на знаки точних рівностей:

1.

2.

3.

Оберемо масштаб осей координат (ледве більше максимальної координати крапок) і побудуємо відповідні прямі:

Щоб визначити ОДР, у кожну конкретну нерівність необхідно підставити координати довільної крапки (найпростіше взяти крапку 0;0) і перевірити істинність отриманої нерівності. Якщо нерівність вірно, то припустимо напівплощину, що містить дану крапку, інакше - інша напівплощина. ОДР являє собою частина площини, що належить одночасно всім припустимим областям нерівностей. Якщо ОДР відсутній, то Ви повинні зробити висновок, що завдання не має рішення. У нашім випадку ОДР буде мати такий вигляд:

Далі - будуємо графік цільової функції. Особливістю цього графіка є відсутність конкретного рівняння, замість якого вказується лише пріоритетне устремління. У такому випадку використовують поняття "лінії рівня", що означає безліч паралельних прямих, що відповідають вираженню виду:

Спочатку ми побудуємо одну довільну лінію рівня для нашої цільової функції. Для цього приведемо рівняння цільової функції до виду:

де c - довільне число.

Прим.: значення з доцільно встановлювати таким чином, щоб пряма пройшла близько до середини зображених координатних відрізків.

Таким чином, по суті, ми встановлюємо деяке вихідне припущення про значення цільової функції.

У нашому випадку зручно використовувати c = 4000, тоді:

Далі необхідно побудувати вектор з координатами (a;b) на основі вираження цільової функції. (Вектор - це напівпряма, що починається із крапці (0;0) і проходить через крапку (a;b). Якщо пряма, що відповідає цільової функції, і вектор побудовані вірно, то на графіку вони будуть перпендикулярними.

У нашім випадку вектор буде мати координати: (100;21,25).

Даний вектор допоможе нам, пересуваючи лінію рівня, знайти крапку оптимуму. Напрямок вектора збігається з напрямком зростання цільової функції (і навпаки). Тому пошук крапки оптимуму А^*(х1^*;х2^*) провадитися шляхом паралельного переміщення лінії рівня уздовж вектора. Якщо Ви досить точно побудуєте графіки всіх прямих, то для переміщення прямої рівня зручно використовувати дві креслярські лінійки.

Оптимальне значення завжди перебуває на границі ОДР. Тому остання по ходу руху вершина ОДР буде крапкою оптимуму. У деяких випадках, коли лінії рівня паралельні графікові одного з обмежень, може бути визначена не єдина, а безліч крапок оптимуму. Якщо у Вас зустрітися така ситуація, ви повинні будете зробити відповідний висновок.

У нашім прикладі крапка оптимуму перебувати у вершині ОДР, утвореної перетинанням обмежень 1 і 2 (по площі залу й продавцям):

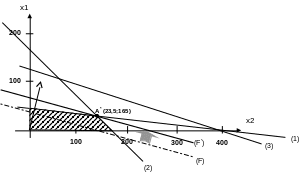Щоб визначити точні координати крапки оптимуму, необхідно вирішити відповідну систему рівнянь:

Підставивши ці значення у вираження цільової функції ми одержимо:

Т.ч. робимо висновок, що оптимальними асортиментами для підприємства є 24 кухонних комбайна й 165 міксерів. У цьому випадку підприємство одержить 5906,25 грн. маржинального прибутку.

Прим.: координати крапки, що відповідають рішенню завдання варто округляти до одиниць, кратним можливим продажним партіям товарів (у нашім випадку - 1 шт.).

Для визначення поточного "вузького місця" підприємства необхідно візуально проаналізувати: зниження дії якого обмеження дозволить домогтися підвищення значення цільової функції (дозволить розширити ОДЗ таким чином, щоб пересунути лінію рівня цільової функції по напрямку вектора).

Очевидно, що в нашім прикладі таким обмеженням буде обмеження 1 - обмеження по продавцях. Однак важливо ще й визначити, наскільки доцільно розширювати дане "вузьке місце". Тут можливо дві ситуації:

• на деякому етапі розширення даного обмеження почне діяти інше обмеження й подальші дії не принесуть ніякого ефекту, "вузьким місцем" стане інше обмеження; у цьому випадку "вузьке місце варто розширити до моменту початку дії іншого обмеження;

• іноді розширювати вузьке місце можна до ∞ і при цьому одержувати позитивний ефект (така ситуація можлива лише в чинність спрощеності розв'язуваного завдання, у житті вона не зустрічається); у такому випадку Вам необхідно розширити "вузьке місце" у два рази й зробити відповідний висновок.

У нашому прикладі обмеження 1 треба "підсунути" до крапки, де пряма, що відповідає обмеженню 3 перетинається з віссю x1 (120;0). Далі цієї крапки обмеження переміщати недоцільно, оскільки це не принесе ніякого ефекту. Р озширена ОДЗ зображена на малюнку:

Модифікуємо обмеження (1) таким чином, щоб відповідна йому пряма проходила через крапку (120;0):

Зміна обмеження відповідає управлінському рішенню підвищити площа розміщення товарів з 20 до 60 м². Використовуючи збільшену ОДЗ, оптимізуємо знову наші асортименти (спосіб аналогічний - переміщення лінії рівня цільової функції уздовж вектора)

У цьому випадку крапкою оптимуму буде крапка перетинання прямих, що відповідають обмеженням (1), (3) і цільової функції з віссю x1 (120;0). Використовуючи координати цієї крапки, визначимо значення цільової функції:

Т.ч. робимо висновок, що рішення розширити торговельну площу з 20 до 60 м² при асортименті реалізованої продукції:

• кухонних комбайнів - 120 шт;

• міксерів - 0 шт.

Дозволить підприємству одержати 12000 грн маржинального прибутку (у порівнянні з 5906,25 грн - у попередньому варіанті).

Прим.: у випадку, коли в чинність дрібного масштабу або неточної побудови графіка, необхідне рішення неочевидне, варто піддавати перевірці всі можливі рішення, наприклад, у нашім прикладі було складно визначити, яка із двох крапок: A або B є більше вигідною для підприємства:

Тому було необхідно розрахувати значення цільової функції для кожної із цих крапок і вибрати з них ту, значення цільової функції в якій більше.

Для розробки варіанта завдання вихідних даних студент використовує буквенно-цифрову систему кодів: букви (стрічка в таблиці вихідних даних)- прізвище, ім'я, по батькові; цифри-

порядковий номер стовбця в таблиці.

Приклад:

Ф.і.о. (рядок) И В А Н О В И В А Н И В А Н О №стовб. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15