
- •Основные понятия и определения.
- •Отображения, осуществляемые основными элементарными функциями.
- •Линейная функция.
- •Функция .
- •Дробно-линейная функция.
- •Показательная функция .
- •Логарифмическаяая функция .
- •2.6 Тригонометрические функции.
- •2.7 Функция Жуковского.
- •Отображение окружностей функцией Жуковского.
- •2.8 Гиперболические функции.
- •2.9 Степенная функция , - целое число.
- •2.10 Функция . (15)
- •2.11 Обобщённая степенная функция . (18)
- •2.12 Отображение луночек.
- •§1. Конформные отображения. Основные понятия и определения.
- •§2. Отображения, осуществляемые основными элементарными функциями.
2.10 Функция . (15)
Функция
(15) является обратной к функции
. Пусть
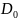 - плоскость
с разрезом вдоль действительной
положительной полуоси. Рассмотрим
функцию
- плоскость
с разрезом вдоль действительной
положительной полуоси. Рассмотрим
функцию
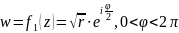 (16).
(16).
Эта
функция однозначна в области
,
и множество её значений – верхняя
полуплоскость

Аналогично
функция
 (17) однозначна, непрерывна в области
,
удовлетворяет условию
и отображает область
на нижнюю полуплоскость
(17) однозначна, непрерывна в области
,
удовлетворяет условию
и отображает область
на нижнюю полуплоскость
 .
.
Таким образом, функция двузначна.
Обе
функции
 и
и
 дифференцируемы и аналитичны в области
,
так как
дифференцируемы и аналитичны в области
,
так как
 ,
k=1;2
,
k=1;2
Функции
и
называются аналитическими ветвями
двузначной функции
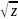 в области
.
Для конкретизации рассматриваемой
ветви обычно указывают значение функции
в какой-либо внутренней точке
,
либо значение функции в какой-нибудь
граничной точке. Так как
в области
.
Для конкретизации рассматриваемой
ветви обычно указывают значение функции
в какой-либо внутренней точке
,
либо значение функции в какой-нибудь
граничной точке. Так как
 и
и
 ,
то точки
и
называются точками ветвления.
,
то точки
и
называются точками ветвления.
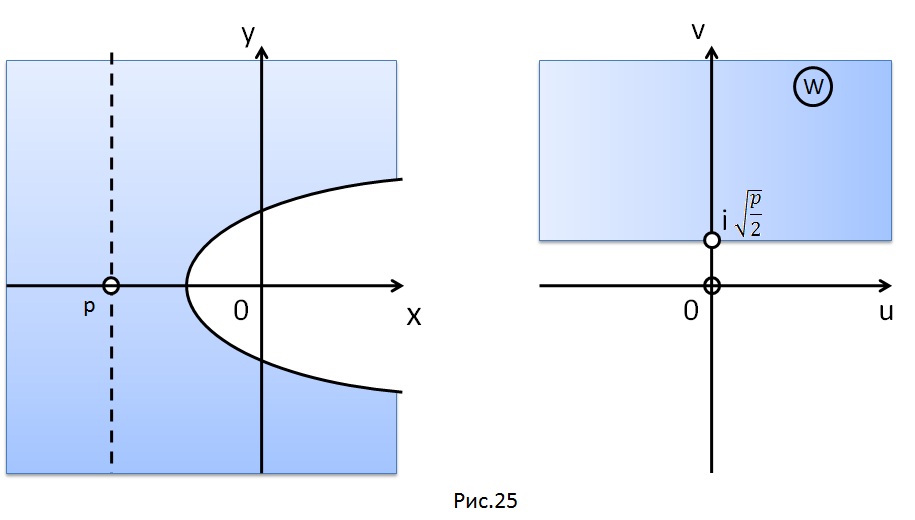
Пусть
– область, расположенная вне параболы
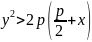 .
В этой области функция
распадается на две аналитические ветви
и
.
В этой области функция
распадается на две аналитические ветви
и
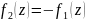 ,
где
,
где
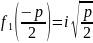 . Тогда функция
. Тогда функция
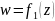 конформно отображает область
на полуплоскость
конформно отображает область
на полуплоскость
 (рис. 25), а функция
(рис. 25), а функция
 - на полуплоскость
- на полуплоскость
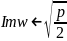 .
.
Функция
 ,
обратная к степенной функции
является
,
обратная к степенной функции
является
-значной,
то есть каждому значению
,
и
 отвечает
значений
,
которые вычисляются по формуле
отвечает
значений
,
которые вычисляются по формуле
 или
или
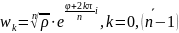 .
.
Каждое
из значений
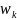 образует ветвь многозначной функции
.
Точкой ветвления функции является
точка
.
На плоскости
с разрезом вдоль положительной полуоси
образует ветвь многозначной функции
.
Точкой ветвления функции является
точка
.
На плоскости
с разрезом вдоль положительной полуоси
 можно выделить
однозначных ветвей
.
Такие ветви однолистно отображают
плоскость
с разрезом вдоль положительной
действительнойполуоси на секторы
можно выделить
однозначных ветвей
.
Такие ветви однолистно отображают
плоскость
с разрезом вдоль положительной
действительнойполуоси на секторы

2.11 Обобщённая степенная функция . (18)
Такая функция является сложной, и её свойства существенно зависят как от значений , так и от . Будем в основном полагать, что – действительное положительное число.
Функцию
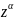 можно
представить следующим образом:
можно
представить следующим образом:
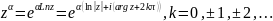
Из свойств логарифма вытекают следующие свойства степенной функции:
Функция - аналитическая в кольце
 .
.Производная степенной функции вычисляется по формуле
 .
.
Любые два элемента и в каждой точке и отличаются числовым множителем
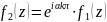 (19)
(19)Все значения функции при действительном значении в точке
 задаются
формулой
задаются
формулой

При действительных функция
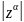 однозначна:
однозначна:
 .
(21)
.
(21)
В каждой односвязной области, не содержащей точек и , функция распадается на аналитические ветви. Одна из этих ветвей, при действительном , определяется формулой
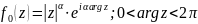 (22)
(22)
Остальные
ветви имеют вид
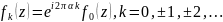 (22)
(22)
Пусть
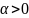 и
и
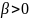 таковы, что
таковы, что
 . Тогда
ветвь
(21) функции
взаимно однозначно отображает сектор
. Тогда
ветвь
(21) функции
взаимно однозначно отображает сектор
 на сектор
на сектор
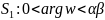 (рис.
26) , то есть
разворачивает сектор
(рис.
26) , то есть
разворачивает сектор
 в
раз.
в
раз.
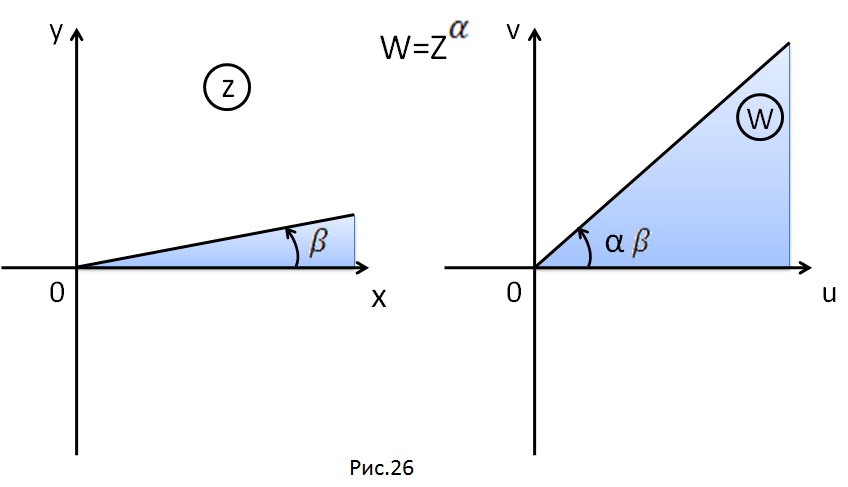
Следствие
: Пусть
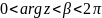 .
Тогда
функция
.
Тогда
функция
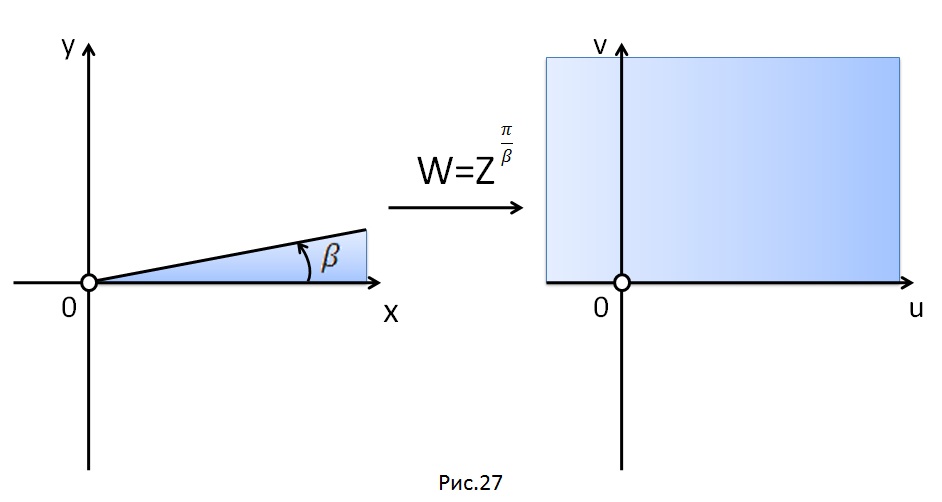
 конформно отображает угол
на верхнюю полуплоскость
(рис. 27).
конформно отображает угол
на верхнюю полуплоскость
(рис. 27).
2.12 Отображение луночек.
Определение.
Область
 ,
ограниченная двумя дугами окружностей,
пересекающихся в точках
и
,
под одним и тем же углом
,
называется луночкой
(рис.
28).
,
ограниченная двумя дугами окружностей,
пересекающихся в точках
и
,
под одним и тем же углом
,
называется луночкой
(рис.
28).
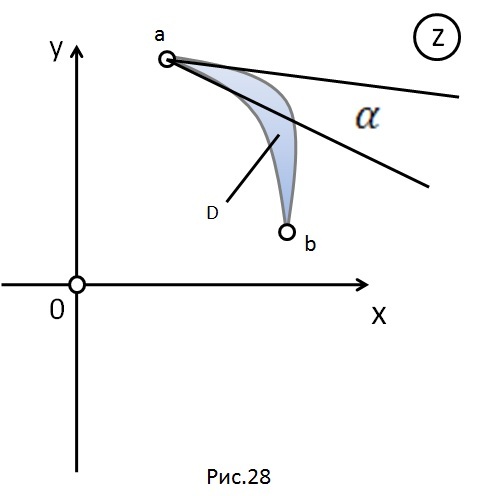
Луночку можно конформно отобразить на верхнюю полуплоскость с помощью дробно–линейной и степенной функции следующим образом:
С помощью дробно–линейного преобразования
 отобразим точку
в ноль
отобразим точку
в ноль
 ,
а точку
- в бесконечно удалённую точку
,
а точку
- в бесконечно удалённую точку
 .
Это отображение переводит дуги,
ограничивающие область
,
в лучи, пересекающиеся в точке
под углом
.
Образом луночки в
является
угол
.
Это отображение переводит дуги,
ограничивающие область
,
в лучи, пересекающиеся в точке
под углом
.
Образом луночки в
является
угол
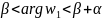 ,
где
,
где
 - некоторое число.
- некоторое число.
Угол
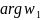 поворотом
поворотом
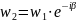 отображаем на угол
отображаем на угол
 .
.
Функция
 отображает угол
на полуплоскость
.
отображает угол
на полуплоскость
.
Таким
образом, функция
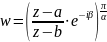 (23)
(23)
Конформно отображает луночку на верхнюю полуплоскость
.
Пример
7. Отобразить
луночку
 (рис. 29) на верхнюю полуплоскость.
(рис. 29) на верхнюю полуплоскость.
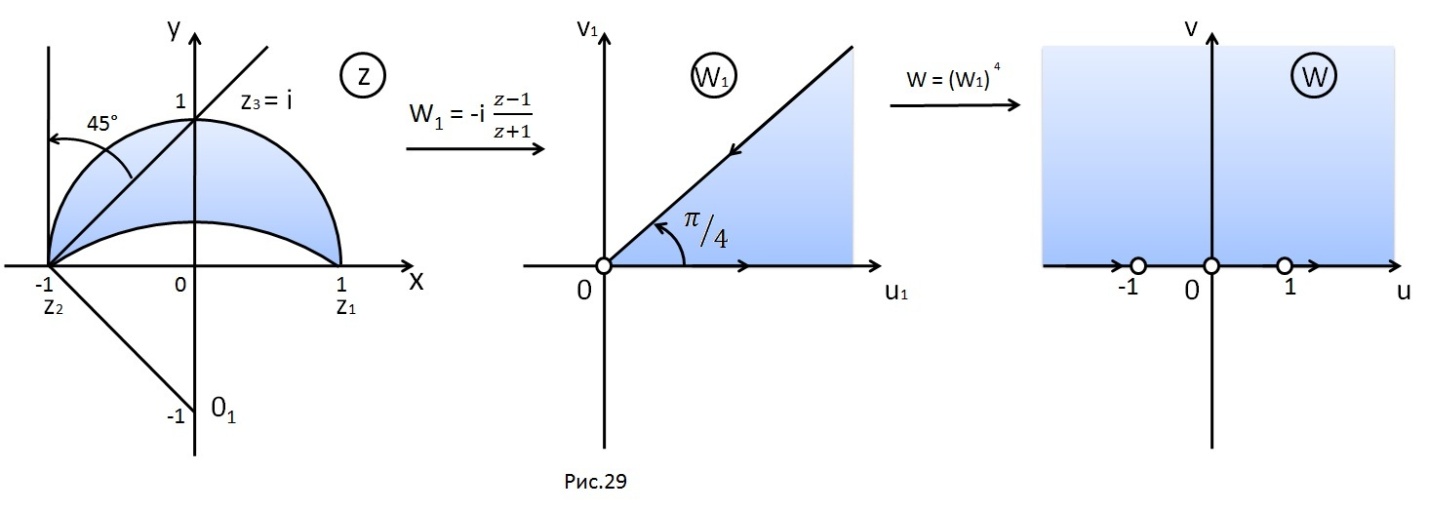
Решение:
данные окружности пересекаются в точках:

 под углом
под углом
 .
С помощью дробно-линейной функции
.
С помощью дробно-линейной функции
 отобразим точку
в ноль, а точку
- в бесконечность. Коэффициент
отобразим точку
в ноль, а точку
- в бесконечность. Коэффициент
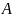 определим, потребовав, чтобы точка
определим, потребовав, чтобы точка
 отобразиться в точку
отобразиться в точку
 из выражения:
из выражения:
 .
.
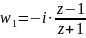 -
вспомогательная функция, отображающая
область
на угол плоскости
,
ограниченный положительной полуосью
и полупрямой
-
вспомогательная функция, отображающая
область
на угол плоскости
,
ограниченный положительной полуосью
и полупрямой
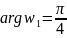 ,
что следует из соответствия обхода
границ и сохранения углов. Возвысив
в четвёртую степень, «развернём» её на
плоскость
,
что следует из соответствия обхода
границ и сохранения углов. Возвысив
в четвёртую степень, «развернём» её на
плоскость
.
Ответ: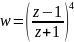
Пример
8. Отобразить
луночку
 (рис. 30) на верхнюю полуплоскость.
(рис. 30) на верхнюю полуплоскость.
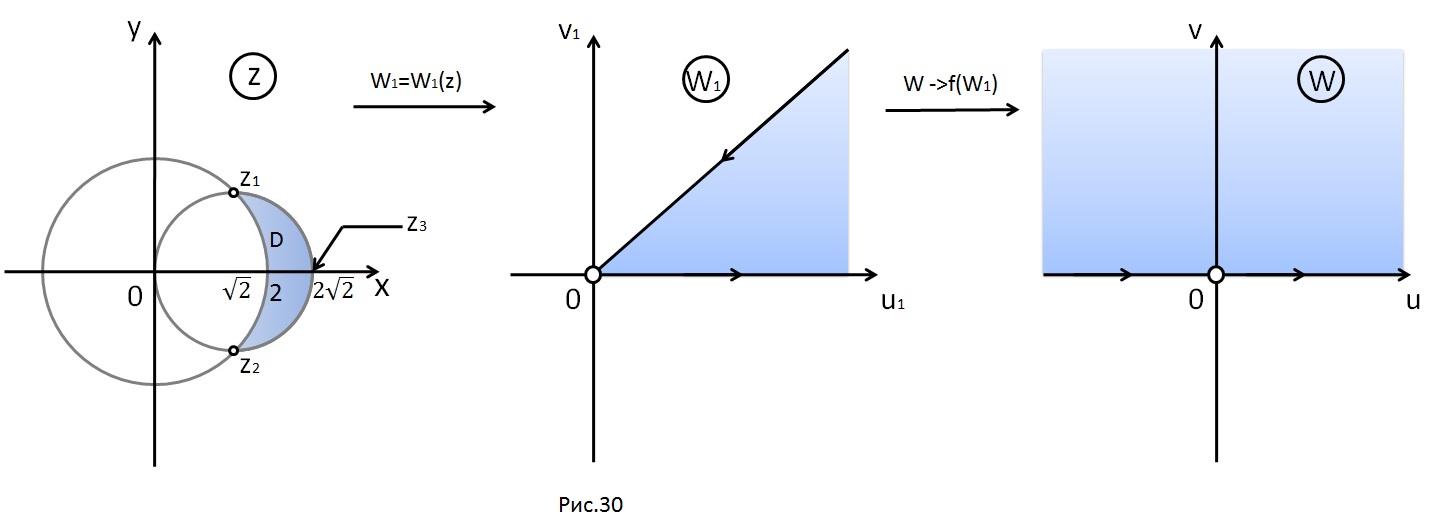
Решение.
Найдём точки пересечения дуг окружностей,
ограничивающих луночку:

 .
.
Здесь
угол между касательными к кривым также
равен
 ,
обход области
совершаем в положительном направлении.
Отобразим точку
в ноль, а точку
- в бесконечность функцией
,
обход области
совершаем в положительном направлении.
Отобразим точку
в ноль, а точку
- в бесконечность функцией
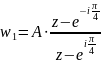 .
Коэффициент
находим из условия
.
Коэффициент
находим из условия
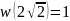 ,
отобразив точку
,
отобразив точку
 в точку
.
в точку
.
 .
.
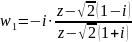 -
вспомогательная функция, отображающая
часть границы луночки
-
вспомогательная функция, отображающая
часть границы луночки
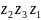 в положительную полуось действительной
оси, а часть границы
в положительную полуось действительной
оси, а часть границы
 в полупрямую
.
Степенная функция
в полупрямую
.
Степенная функция
 отображает полученный угол на верхнюю
полуплоскость
.
отображает полученный угол на верхнюю
полуплоскость
.
Ответ: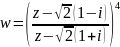
Задачи для самостоятельного решения.
Отобразить на верхнюю полуплоскость часть плоскости, расположенную вне двух окружностей
 .
.Найти функцию, отображающую луночку
 на
полосу
на
полосу
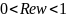 .
.
Отобразить полосу
 на первый квадрант
на первый квадрант
 .
.Найти область плоскости , на которую функция
 отображает четверть круга
отображает четверть круга
 .
.Конформно отобразить область
 на
верхнюю полуплоскость
.
на
верхнюю полуплоскость
.
Определить дробно-линейную функцию, отображающую круг
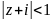 в круг
в круг
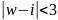 так, чтобы точка
так, чтобы точка
 перешла в точку
перешла в точку
 .
.Отобразить луночку
 на полуплоскость
на полуплоскость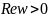 .
.Отобразить на верхнюю полуплоскость полуполосу
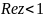 ,
,
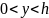 .
.Отобразить на верхнюю полуплоскость полуполосу
 ,
.
,
.
Ответы к задачам для самостоятельного решения.
 .
Дробно-линейным
преобразованием отобразить обе
окружности в прямые: левую – в
вещественную ось, при этом правая
окружность отображается в прямую
.
Дробно-линейным
преобразованием отобразить обе
окружности в прямые: левую – в
вещественную ось, при этом правая
окружность отображается в прямую
 .
Далее горизонтальную полосу расширить
до величины
и
отобразить её на верхнюю полуплоскость.
.
Далее горизонтальную полосу расширить
до величины
и
отобразить её на верхнюю полуплоскость.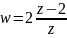 .
. .
.Верхний полукруг
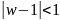 ,
.
,
. .
.Отображение осуществляется функцией, удовлетворяющей соотношению
 ,
– некоторая
действительная постоянная.
,
– некоторая
действительная постоянная.Функция
 отображает
исходную
луночку в угол, ограниченный двумя
ортогональными прямыми , расположенными
в полуплоскости
отображает
исходную
луночку в угол, ограниченный двумя
ортогональными прямыми , расположенными
в полуплоскости
 и наклоненными к действительной оси
под углами
и наклоненными к действительной оси
под углами
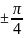 .
Функция
.
Функция
 переводит
этот угол в правую полуплоскость. Ответ:
переводит
этот угол в правую полуплоскость. Ответ:
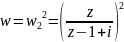
 .
.Функция
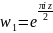 отображает
данную полуполосу в полукруг
отображает
данную полуполосу в полукруг
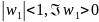 .
Функция Жуковского
.
Функция Жуковского
 переводит этот полукруг в нижнюю
полуплоскость
переводит этот полукруг в нижнюю
полуплоскость
 .
Поэтому функция
.
Поэтому функция
 решает поставленную задачу.
решает поставленную задачу.
Список рекомендуемой литературы.
Морозова В. Д. Теория функции комплексного переменного. М. Изд-во МГТУ им. Н. Э. Баумана 2000, 520с.
Копаев А. В., Садыхов Г. С., Теория функции комплексного переменного. М. Изд-во МГТУ им. Н. Э. Баумана 1992, 102с.
М.П. Краснов, А. И. Киселёв, Г. И. Макаренко Функции комплексного переменного. Операционное исчисление. Теория устойчивости. М. Наука, 1981, 304с.
А. В. Абрагин, В. М. Дубровин Теория функции комплексного переменного. М. Изд-во МГТУ им. Н. Э. Баумана 2006, 80с.
Оглавление.
