
- •Основные понятия и определения.
- •Отображения, осуществляемые основными элементарными функциями.
- •Линейная функция.
- •Функция .
- •Дробно-линейная функция.
- •Показательная функция .
- •Логарифмическаяая функция .
- •2.6 Тригонометрические функции.
- •2.7 Функция Жуковского.
- •Отображение окружностей функцией Жуковского.
- •2.8 Гиперболические функции.
- •2.9 Степенная функция , - целое число.
- •2.10 Функция . (15)
- •2.11 Обобщённая степенная функция . (18)
- •2.12 Отображение луночек.
- •§1. Конформные отображения. Основные понятия и определения.
- •§2. Отображения, осуществляемые основными элементарными функциями.
2.8 Гиперболические функции.
Гиперболический
косинус
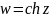 .
.
Используя
формулу
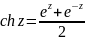 ,
обозначим:
,
обозначим:
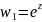 ,
тогда получим:
,
тогда получим:
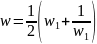 ,
то есть
является суперпозицией двух функций.
В результате последовательного
отображения
,
а затем отображения
получаем отображение, осуществляемое
функцией
.
,
то есть
является суперпозицией двух функций.
В результате последовательного
отображения
,
а затем отображения
получаем отображение, осуществляемое
функцией
.
В
частности, функция
конформно отображает полуполосу
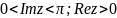 на верхнюю полуплоскость
(рис. 19).
на верхнюю полуплоскость
(рис. 19).
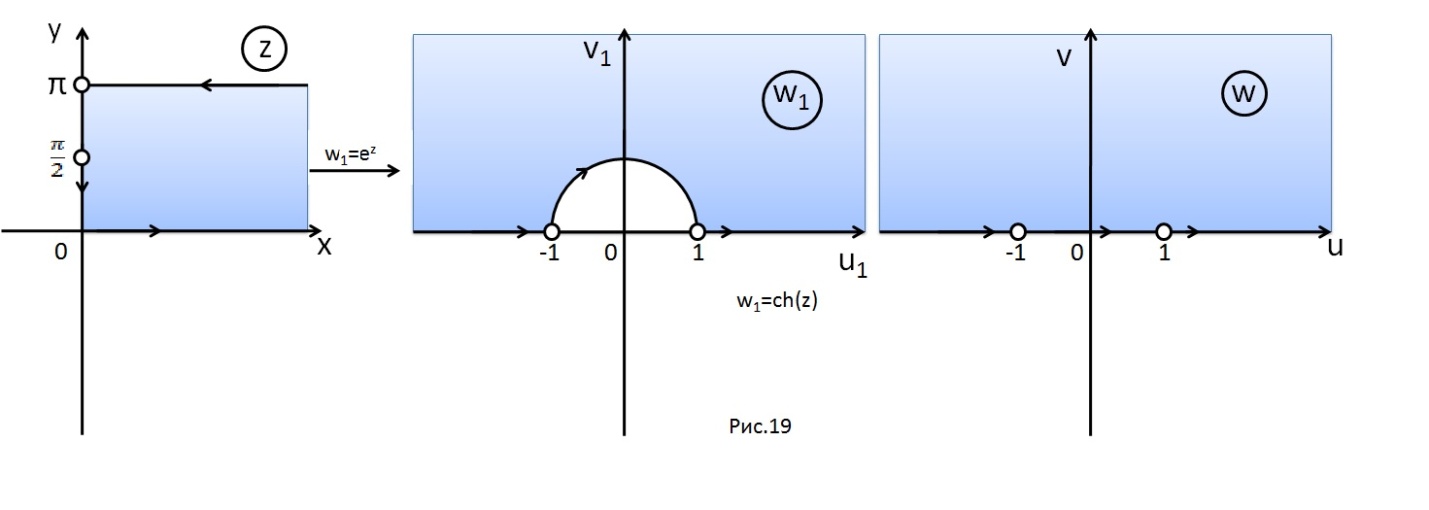
Отметим,
что
,
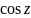 ,
,
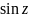 ,
,
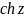 ,
,
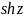 связаны между собой известными
выражениями. Например, функция
связаны между собой известными
выражениями. Например, функция
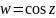 конформно отображает полуполосу
конформно отображает полуполосу
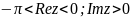 на верхнюю полуплоскость
.
на верхнюю полуплоскость
.
В
самом деле:
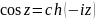 и следует выполнить сначала преобразование
и следует выполнить сначала преобразование
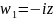 (поворот относительно точки
на угол
(поворот относительно точки
на угол
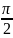 по часовой стрелке), а затем отобразить
функцией
по часовой стрелке), а затем отобразить
функцией
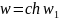 .
В результате получим отображение
(рис. 20).
.
В результате получим отображение
(рис. 20).
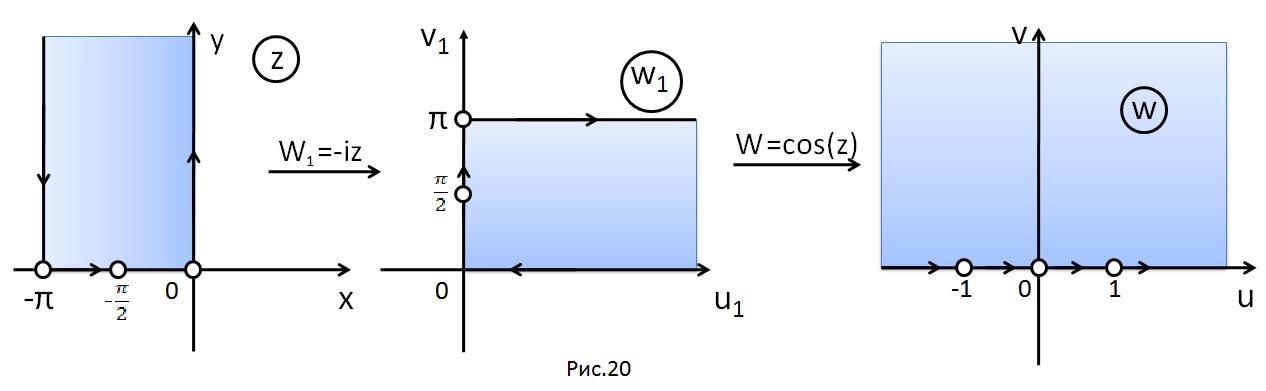
Тогда
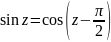 ,
полагая
,
полагая
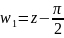 ,
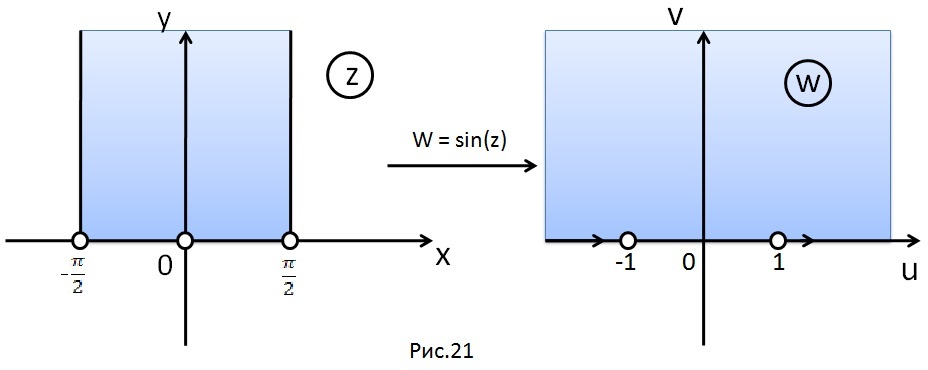
получим, что функция
конформно отображает полуполосу
,
получим, что функция
конформно отображает полуполосу
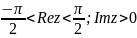 на верхнюю полуплоскость
(рис. 21).
на верхнюю полуплоскость
(рис. 21).
Гиперболический
синус
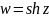 .
.
Воспользуемся
формулой
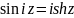 .
Преобразование
.
Преобразование
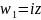 - это поворот вокруг точки
на угол
против часовой стрелки. Если осуществить
такой поворот для полуполосы
- это поворот вокруг точки
на угол
против часовой стрелки. Если осуществить
такой поворот для полуполосы
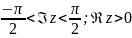 ,
а затем применить преобразование
,
а затем применить преобразование
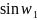 ,
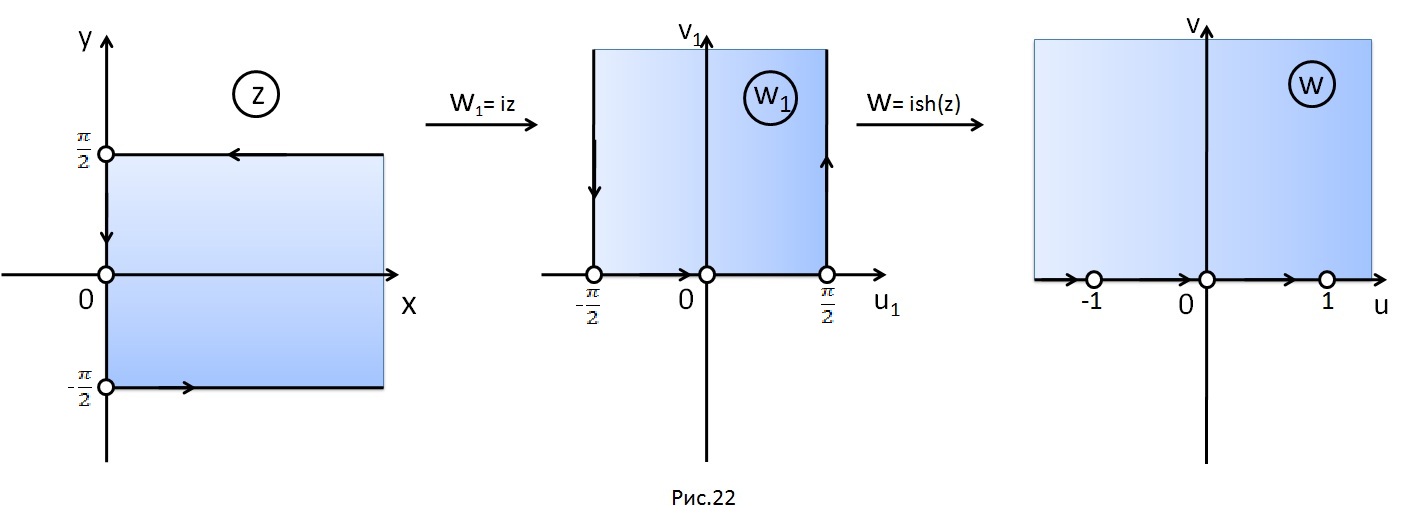
то получим преобразование указанной
полуполосы в верхнюю полуплоскость,
производимую функцией
,
то получим преобразование указанной
полуполосы в верхнюю полуплоскость,
производимую функцией
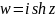 (рис. 22).
(рис. 22).
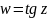 .
.
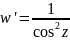 - функция конформно отображает полосу
- функция конформно отображает полосу
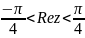 на
единичный круг
.
Это отображение удовлетворяет условиям
на
единичный круг
.
Это отображение удовлетворяет условиям
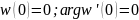 .
Преобразуем выражение следующим образом
:
.
Преобразуем выражение следующим образом
:
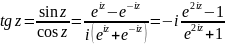 .
.
Тогда,
отображение
можно рассматривать как суперпозицию
трёх отображений: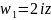 ,
,
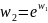 ,
,
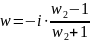 .
.
Последовательное выполнение этих трёх преобразований приводит к искомому отображению.

Первые
два преобразования переводят заданную
полосу в полуполосу
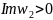 ,
а дробно-линейное преобразование
,
а дробно-линейное преобразование
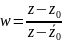 ,
,
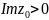 ,
переводит эту полуплоскость на круг
.
,
переводит эту полуплоскость на круг
.
2.9 Степенная функция , - целое число.
Для наглядности рассмотрим сначала функцию (11). Функция однолистна в области , если эта область не содержит ни одной пары точек, симметричных относительно точки . Функция однолистна в верхней полуплоскости , или в нижней полуплоскости .
Пусть
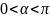 ,
тогда луч
расположен в верхней полуплоскости и
при отображении (11) этот луч переходит
в луч
,
тогда луч
расположен в верхней полуплоскости и
при отображении (11) этот луч переходит
в луч
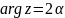 .
Тогда, если луч на плоскости
.
Тогда, если луч на плоскости
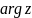 опишет верхнюю полуплоскость, его образ
опишет всю плоскость
.
При этом, лучи
опишет верхнюю полуплоскость, его образ
опишет всю плоскость
.
При этом, лучи
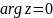 и
перейдут соответственно в лучи
и
перейдут соответственно в лучи
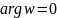 и
и
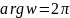 ,
которые геометрически совпадают друг
с другом на положительной действительной
полуоси. Для обеспечения однозначности
отображения на границе области проводят
в плоскости
по положительной полуоси разрез и
считают, что луч
,
которые геометрически совпадают друг
с другом на положительной действительной
полуоси. Для обеспечения однозначности
отображения на границе области проводят
в плоскости
по положительной полуоси разрез и
считают, что луч
отображается на верхний берег разреза, а луч - на нижний берег разреза. Таким образом, функция (11) однолистна в верхней полуплоскости и отображает эту область на плоскость с разрезом вдоль положительной полуоси (рис. 24).
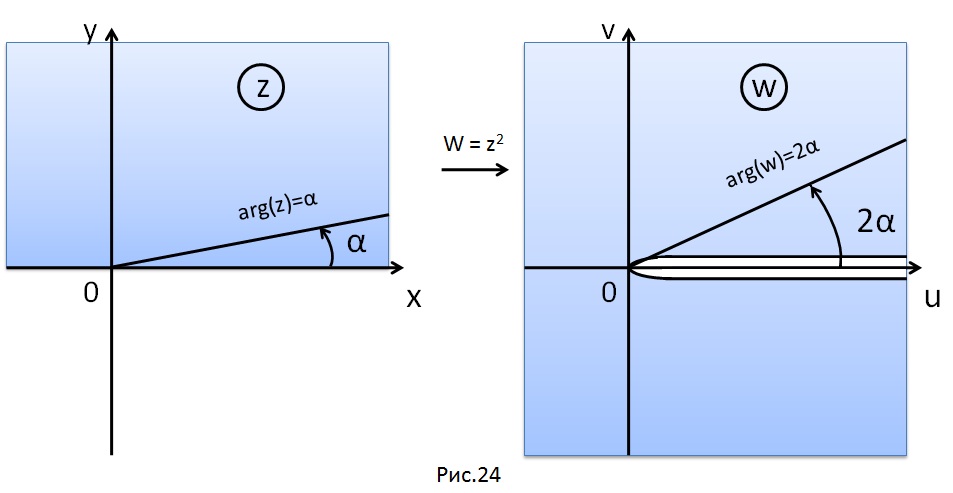
Функция
однолистна и в нижней полуплоскости
и отображает эту область на плоскость
с разрезом вдоль положительной полуоси
(рис. 24). При этом луч
переходит в верхний берег разреза, а
луч
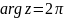 переходит в нижний берег разреза.
переходит в нижний берег разреза.
При
отображении
правая полуплоскость
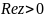 переходит в плоскость с разрезом по
отрицательной действительной полуоси.
Левая полуплоскость
переходит в плоскость с разрезом по
отрицательной действительной полуоси.
Левая полуплоскость
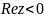 также переходит в плоскость
с разрезом по отрицательной действительной
полуоси.
также переходит в плоскость
с разрезом по отрицательной действительной
полуоси.
Итак, функция взаимно однозначно переводит:
а)
луч
в луч
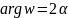 ;
;
б)
дугу окружности
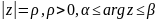 ,
где
,
где
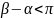 в дугу окружности
в дугу окружности
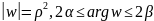 ;
;
в) кольцевой сектор – в кольцевой сектор;
г)
прямые
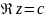 ,
,
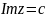 - в параболы
- в параболы
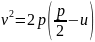 (12) и
(12) и
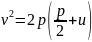 соответственно.
(13)
соответственно.
(13)
Здесь
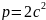 и
.
и
.
При
этом, параболы (12) и (13) пересекаются под
прямым углом и любой прямоугольник в
плоскости
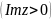 функцией
отображается на криволинейный
четырёхугольник, ограниченный дугами
парабол (12) и (13).
функцией
отображается на криволинейный
четырёхугольник, ограниченный дугами
парабол (12) и (13).
Полученные
выводы легко обобщить на степенную
функцию
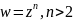 .
(14)
.
(14)
Отображение,
осуществляемое функцией
,
является конформным на всей плоскости,
кроме точек
и
.
Так как
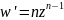 ,
то при
и
,
то при
и
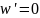 - конформность нарушается. Для обеспечения
однолистности отображения следует
разбить плоскость
на
- конформность нарушается. Для обеспечения
однолистности отображения следует
разбить плоскость
на
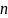 секторов, так как с помощью функции (14)
углы увеличиваются в
раз. Угол
секторов, так как с помощью функции (14)
углы увеличиваются в
раз. Угол
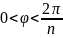 отображается взаимно однозначно на всю
плоскость
с разрезом по положительной части
действительной оси, причём лучу
отображается взаимно однозначно на всю
плоскость
с разрезом по положительной части
действительной оси, причём лучу
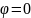 соответствует верхний берег разреза,
а лучу
соответствует верхний берег разреза,
а лучу
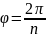 - нижний берег разреза. Такое же отображение
получим для каждого сектора , на которые
плоскость
разбивают лучи
- нижний берег разреза. Такое же отображение
получим для каждого сектора , на которые
плоскость
разбивают лучи
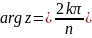 ,
- целое число. При этом при отображении
сектора
,
- целое число. При этом при отображении
сектора
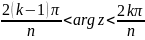 ,
,
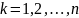 на плоскость с разрезом лучу
на плоскость с разрезом лучу
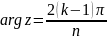 соответствует верхний берег разреза,
а лучу
соответствует верхний берег разреза,
а лучу
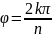 - нижний берег разреза. Из полученных
листов формируют поверхность Римана,
склеивая листы определённым образом.
- нижний берег разреза. Из полученных
листов формируют поверхность Римана,
склеивая листы определённым образом.
