2.7 Функция Жуковского.

Функцией Жуковского называют функцию вида . Функция аналитична всюду, кроме точек и , в которых она имеет полюсы первого порядка.

Производная функции Жуковского.

не равна нулю ни в одной точке, кроме .

Следовательно, отображение, осуществляемое функцией Жуковского, везде конформно, кроме точек . Функция Жуковского однолистна в области только тогда, когда в этой области нет различных точек и , связанных соотношением . (3)

Равенство (3) геометрически означает, что точка получается из точки с помощью инверсии, то есть двойной симметрии относительно окружности и относительно прямой .

Таким образом, функция Жуковского однолистна в любых областях, не содержащих точек, которые получаются одна из другой с помощью инверсии. Примерами таких областей могут быть:

1. - внешность единичного круга;

2. – внутренние точки единичного круга;

3. – верхняя полуплоскость;

4. – нижняя полуплоскость.

Пусть и пусть область, состоящая из точек . Тогда функция Жуковского однолистна в области только тогда, когда области и не имеют общих точек. Так как если , то и при отображении образами областей и будет являться одна и та же область в .

Отображение окружностей функцией Жуковского.

Найдём образ окружности , где - действительное число. Полагая , , получим , откуда

, .(4)

Пусть в плоскости задана окружность (5)

Тогда из (4) следует, что образом окружности при отображении функцией Жуковского будет эллипс

, , . (6)

С полуосями , и с фокусами в точках (так как ). Пусть , тогда, исключая из уравнений (6) получим уравнение эллипса в каноническом виде:

(7)

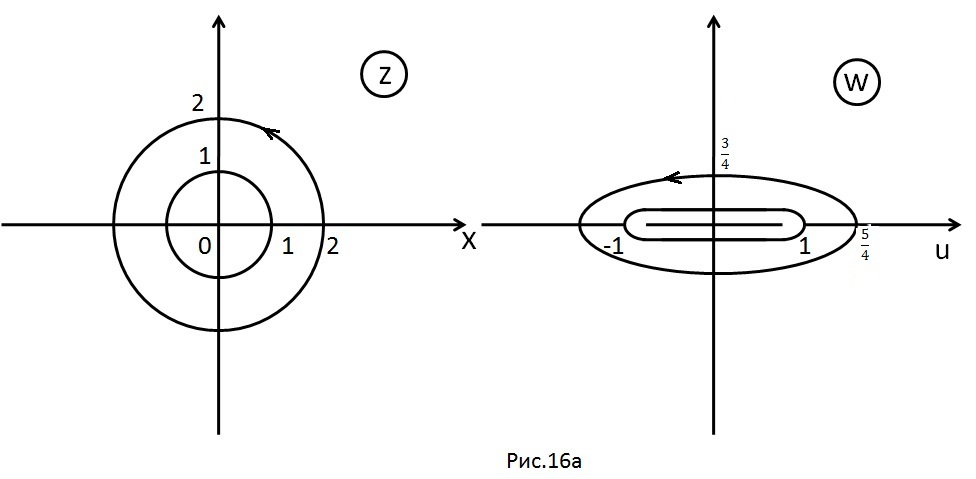
На рисунке 16a окружность , где , ориентированная по часовой стрелке и её образ – эллипс (7), также ориентированный по часовой стрелке.

При эллипс вырождается в отрезок , проходимый дважды.

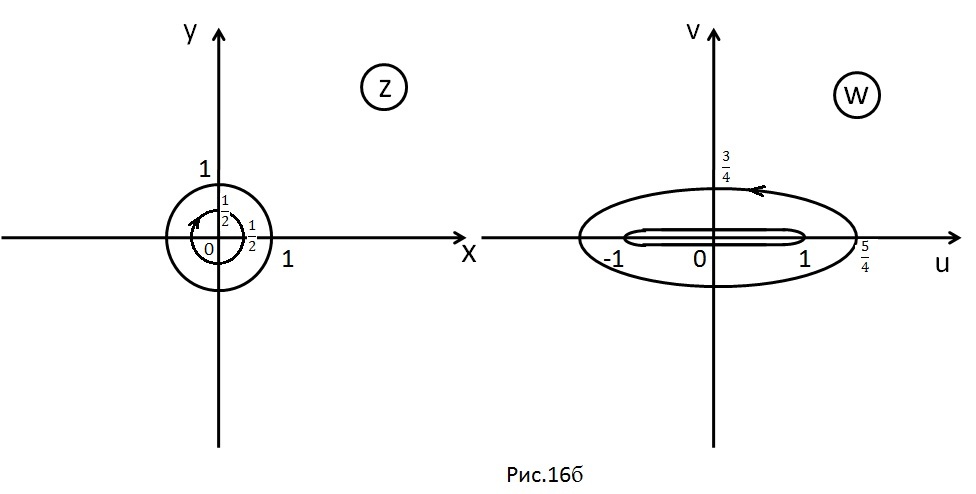
При образы – эллипсы (7), при этом их ориентация меняется на противоположную: окружность , ориентированная по часовой стрелке переходит в эллипс (7), ориентированный против часовой стрелки, а окружность , ориентированная против часовой стрелки переходит в эллипс (7), ориентированный по часовой стрелке (рис.16б).

Принято .

Принято .

Рассмотрим луч , - фиксированное комплексное число. Образом этого луча при отображении функцией Жуковского из формул (6) является кривая

, , (8)

Откуда, исключая параметр , получим: (9)

Кривая (9) – гипербола с фокусами и асимптотами .

Если - кривая (9) является правой ветвью гиперболы. При замене в (8) на получается левая ветвь той же гиперболы. Поэтому луч переходит в правую ветвь гиперболы, а при - в левую ветвь гиперболы. Луч переходит в мнимую ось .

Луч переходит также в мнимую ось . При кривая (7) вырождается в луч проходимый дважды;

луч переходит в луч ;

полуинтервал - в луч ;

луч переходит в луч проходимый дважды.

Вывод: функция Жуковского переводит окружности в эллипсы, а лучи – в ветви гипербол; фокусы всех эллипсов и гипербол расположены в точках ; любой эллипс пересекается с гиперболой под прямым углом.

Пример 6. Найти, во что функция Жуковского переводит область - внешность единичного круга.

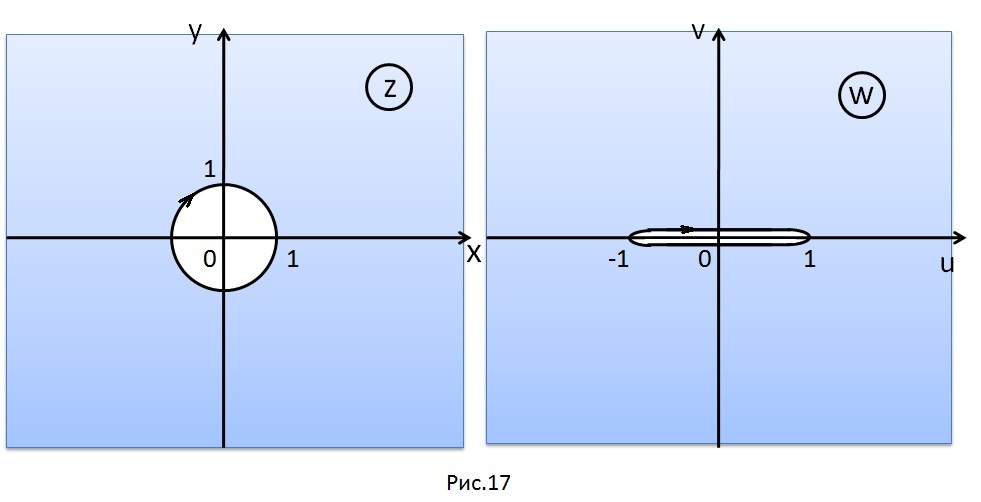
Решение. Функция - однолистная в области . Образами окружностей , где , являются эллипсы, которые заполняют всю область с разрезом по отрезку . Следовательно, функция Жуковского конформно отображает внешность единичного круга на внешность отрезка . При этом окружность , ориентированная по часовой стрелке, переходит в разрез по отрезку , ориентированный по часовой стрелке. При этом полуокружность переходит в верхний берег разреза, а полуокружность переходит в нижний берег разреза.

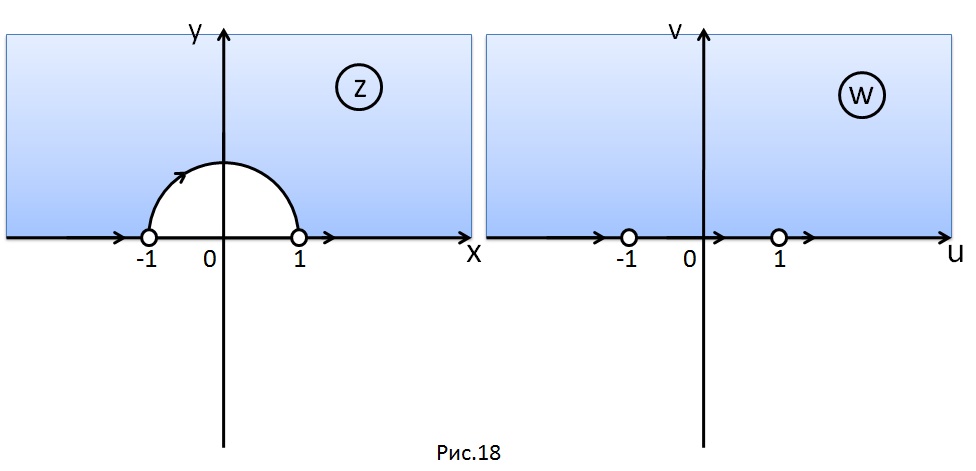
Следствие. Функция Жуковского конформно отображает однолистную область , (рис. 18) на верхнюю полуплоскость .

Решая уравнение относительно , находим , то есть функция (10)

является обратной к функции Жуковского. Отображения функцией (10) являются обратными к отображениям функцией Жуковского.