2. Показательная функция .

Производная функции не обращается в ноль ни в одной точке комплексной плоскости . Отображение, осуществляемое показательной функцией, конформно на всей плоскости , во всякой конечной точке. Выделим действительную и мнимую части функции :

, .

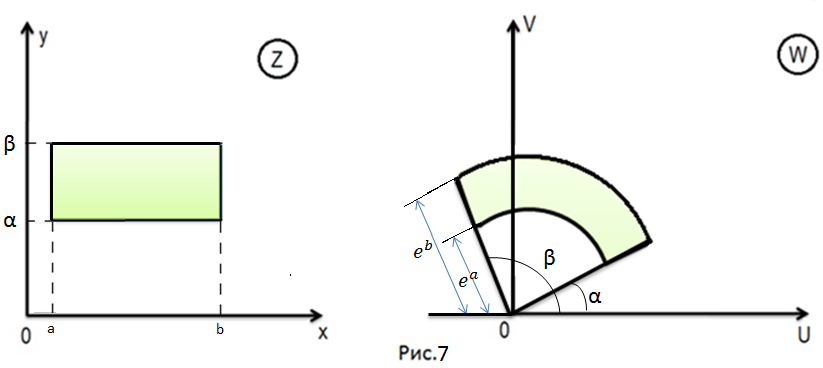
- функция периодическая с чисто мнимым периодом . Функция однозначна, но многолистна, так как обратная ей функция бесконечнозначна. Функция отображает прямоугольник плоскости , определяемый неравенствами , на сектор плоскости , определяемый неравенствами (Рисунок 7) .

Рассмотрим задачу: во что преобразуется полуполоса

с помощью функции ?

Решение.

Положим , .

Так как, по условию, , , то , .

Очевидно, точки , удовлетворяющие этим условиям, заполняют всю плоскость , вне круга с разрезом по оси при

.

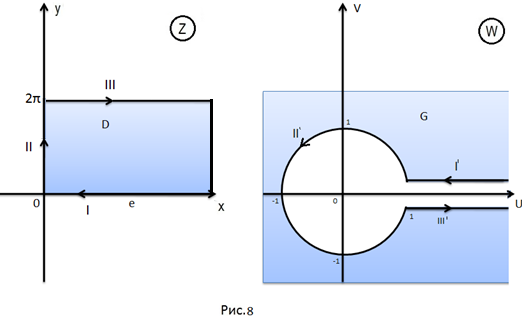
Обходим контур в отрицательном направлении так, чтобы область оставалась справа: сначала по пути , далее по пути

, и по пути .

плоскости будут соответствовать участки

, при этом участок совпадает с верхним, а участок - с нижним краями разреза.

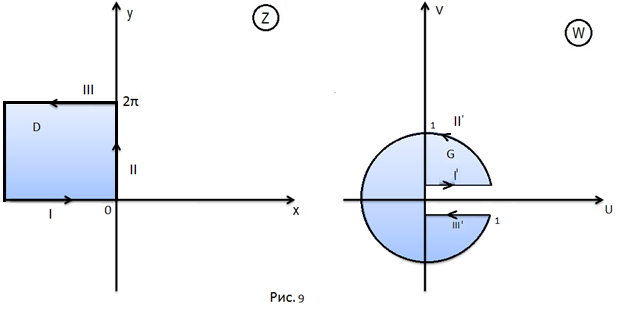
Совершенно аналогично можно показать, что полуполоса с помощью функции преобразуется в круг единичного радиуса с разрезом по оси при .

, , , так что , . Обход области совершаем в положительном направлении,

область остаётся слева.

0

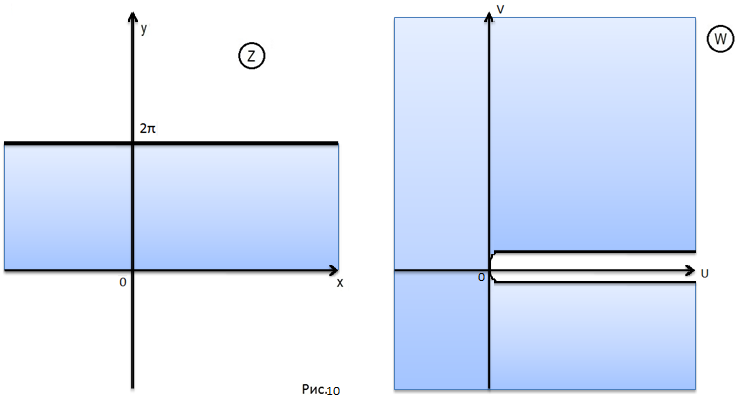
Тогда показательная функция отображает всю полосу на всю расширенную плоскость с разрезом вдоль положительной полуоси (рис.10).

2. Логарифмическаяая функция .

Определяется, как обратная к показательной.

Главное значение логарифма, которое мы и будем рассматривать, соответствует главному значению аргумента и определяется формулой .

Тогда , то есть функция аналитическая во всех конечных точках при , то есть отображение конформно во всех точках

. Так как и , то точки являются точками разветвление функции . Отметим, что любое число обходов вокруг точки не приведёт вновь к первоначальной ветви функции . Такие точки разветвления называются логарифмическими.

Функция осуществляет отображение, обратное функции .

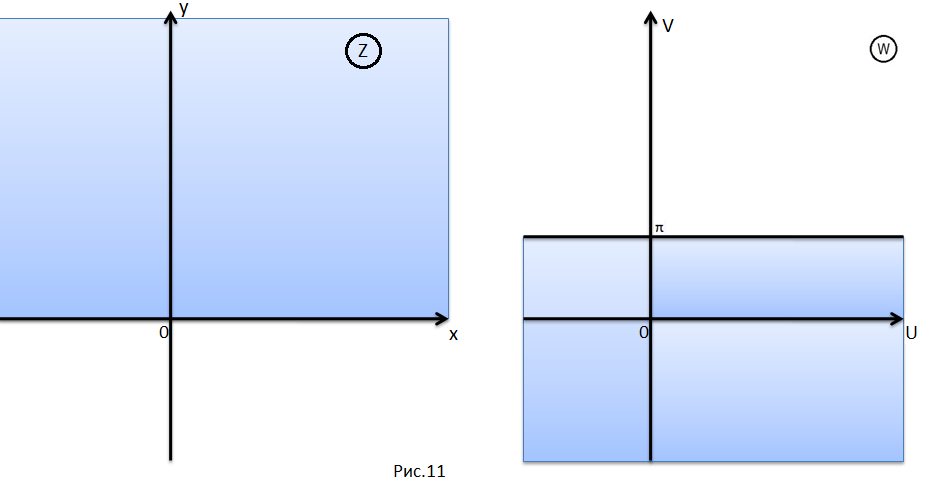
В частности, функция отображает верхнюю полуплоскость плоскости на горизонтальную полосу шириной , то есть на полосу (рис. 11).

0

U

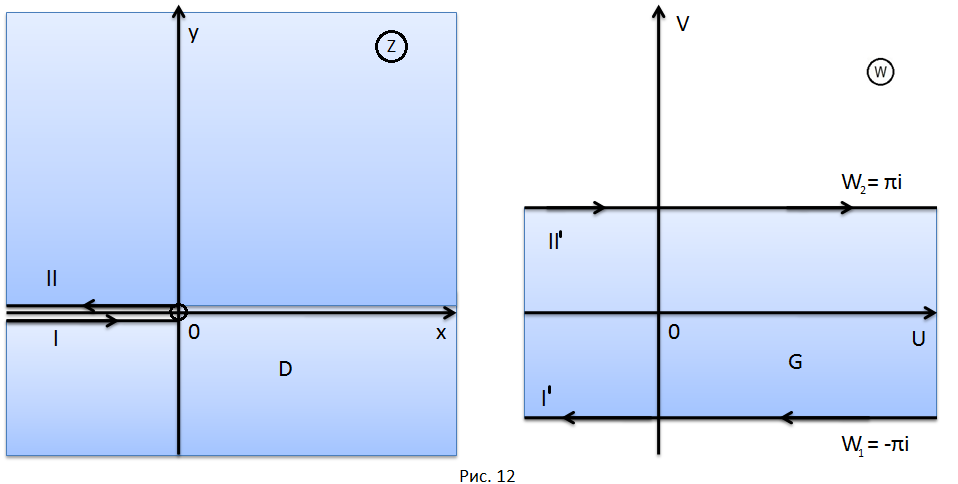
Плоскость с разрезом вдоль отрицательной части действительной оси от точки до точки отображается функцией на полосу плоскости (рис. 12).

Когда точка пробегает по нижнему берегу разреза от до , то в плоскости соответствующая точка опишет линию от точки до точки , .

Когда точка пробегает по верхнему берегу разреза от до , то в плоскости соответствующая точка опишет линию от точки до точки , . При этом область и область остаются справа.

2.6 Тригонометрические функции.

- бесконечнолистная функция комплексной переменной , периодическая с действительным периодом .

Для любого комплексного числа : ,

.

Отсюда следует, что прямую плоскости функция отображает в ветвь гиперболы

(2) на плоскости .

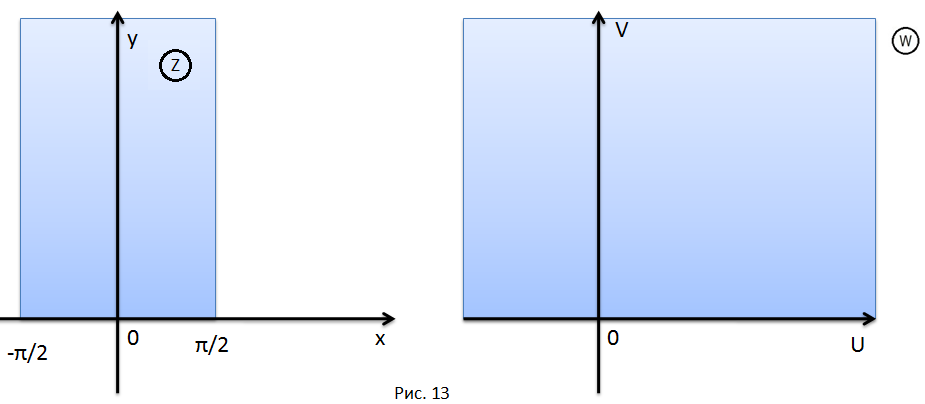
Функция отображает вертикальную полуполосу шириной плоскости , определяемую неравенствами на верхнюю полуплоскость плоскости

бесконечнолистная функция комплексной переменной , периодическая с действительным периодом .

Для любого комплексного числа : ,

.

Отсюда следует, что прямую плоскости функция отображает в ветвь гиперболы

на плоскости .

При прямая переходит в правую ветвь гиперболы, а прямая - в левую ветвь гиперболы.

Все гиперболы софокусны и их фокусы лежат в точках на действительной оси. Прямая отображается на мнимую ось плоскости , а прямые и - в лучи и на действительной оси плоскости . При этом, если точка

пробегает по прямой , то соответствующий луч в плоскости пробегается дважды. Тем самым функция осуществляет взаимно-однозначное отображение полосы плоскости на плоскость с разрезом по лучам действительной оси и . При этом верхняя полуполоса переходит в нижнюю полуплоскость , а нижняя полуполоса переходит в верхнюю полуплоскость (рис.14).

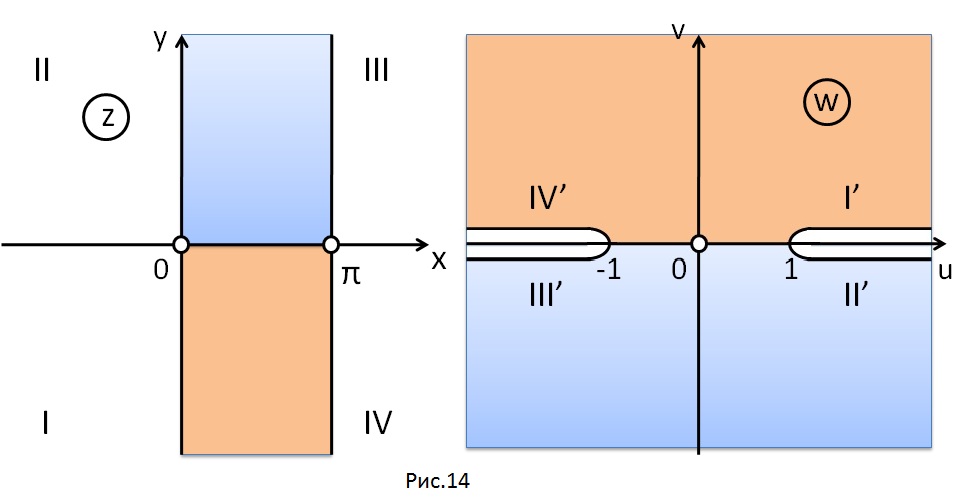
Таким образом, функция отображает нижнюю полуполосу на верхнюю полуплоскость

(рис. 15).