2. Дробно-линейная функция.

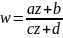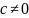, и дискриминант .

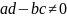Поделив «уголком» числитель функции на её знаменатель, получим:

, где , , .

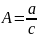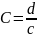Обозначим 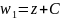- параллельный перенос;

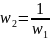- инверсия;

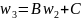- преобразование подобия.

Таким образом, дробно-линейная функция включает три простых преобразования.

С другой стороны, дробно-линейную функцию можно представить следующим образом: 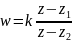, где , , .

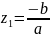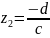Производная дробно-линейной функции не обращается в ноль ни в одной точке плоскости при .

Дробно-линейная функция взаимно однозначно и конформно отображает расширенную плоскость на расширенную плоскость .

Свойства дробно-линейного преобразования.

1. Дробно-линейное преобразование отображает верхнюю полуплоскость 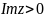на верхнюю полуплоскость

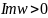
при .

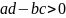2. Дробно-линейное преобразование окружность в плоскости отображает в окружность в плоскости , если считать прямую окружностью бесконечного радиуса. Это круговое свойство дробно-линейной функции.

3. Две точки и , симметричные относительно окружности в плоскости , дробно-линейным преобразованием отображаются в две точки и в плоскости , симметричные относительно окружности 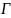, в которую отображается окружность . Это – свойство симметрии дробно-линейного преобразования.

4. Если при дробно-линейном преобразовании окружность или прямая отображаются в окружность и одна из двух точек или симметричных относительно , переходит в центр окружности , то другая точка отображается в бесконечно удалённую точку.

5. Существует единственная дробно-линейная функция, которая переводит три заданные точки , , плоскости в три заданные точки , , плоскости . Такая функция определяется из формулы (1)

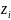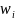
Замечание. Если одна из точек или 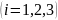является бесконечно удалённой, то в формуле (1) надо заменить единицами те разности, которые содержат эту точку.

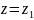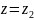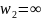6. Если в формуле точки и отображаются соответственно в точки и плоскости , то любая окружность плоскости , проходящая через точку отображается в прямую плоскости . Окружность плоскости , проходящая через точку и через точку , отображается в прямую плоскости , проходящую через начало координат.

Пример 5. Найти дробно-линейную функцию, отображающую сегмент круга, изображённый на рисунке 6, на верхнюю полуплоскость.

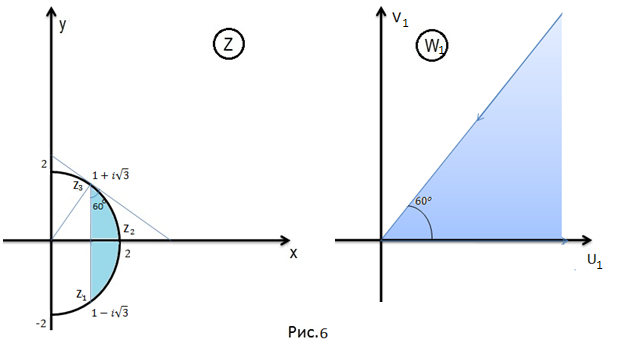
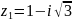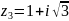Решение. Отобразим точки и плоскости соответственно в точки вспомогательной плоскост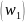и : и 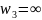с помощью дробно-линейного преобразования: . Подберём коэффициент 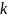так, чтобы точка отобразилась в точку .

.

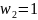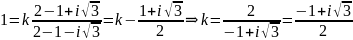Функция 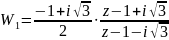отображает заданный сегмент на угол плоскости , ограниченной вещественной осью 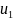и полупрямой

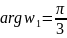, так как дуга сегмента отображается на вещественную положительную полуось, а хорда сегмента – на полупрямую, составляющую угол 60 градусов с положительной полуосью, причём угол отсчитывается в положительном направлении в связи с сохранением направления обхода границ. Далее, полученный угол отображаем на всю верхнюю полуплоскость плоскости , увеличив аргумент полученной функции в три раза, возвысив её в третью степень.

Здесь учтено, что .