
- •Основные понятия и определения.
- •Отображения, осуществляемые основными элементарными функциями.
- •Линейная функция.
- •Функция .
- •Дробно-линейная функция.
- •Показательная функция .
- •Логарифмическаяая функция .
- •2.6 Тригонометрические функции.
- •2.7 Функция Жуковского.
- •Отображение окружностей функцией Жуковского.
- •2.8 Гиперболические функции.
- •2.9 Степенная функция , - целое число.
- •2.10 Функция . (15)
- •2.11 Обобщённая степенная функция . (18)
- •2.12 Отображение луночек.
- •§1. Конформные отображения. Основные понятия и определения.
- •§2. Отображения, осуществляемые основными элементарными функциями.
Конформные отображения.
Основные понятия и определения.
Определение
1. Отображение
окрестности точки
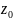 плоскости
плоскости
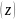 на окрестность точки
на окрестность точки
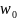 плоскости
плоскости
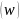 ,
осуществляемое функцией
,
осуществляемое функцией
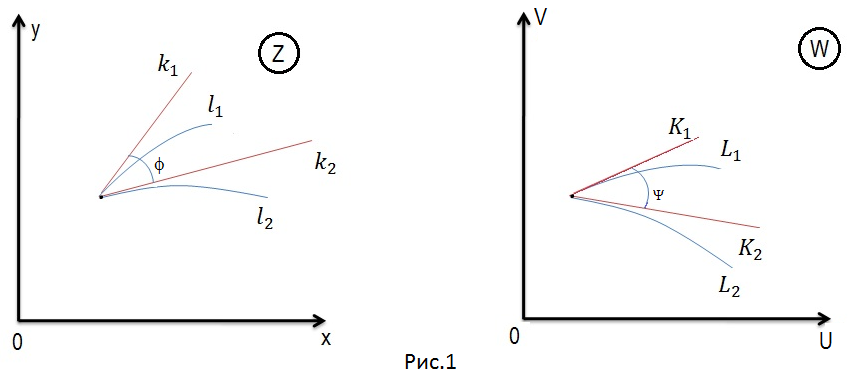
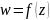 ,
называется конформным, если в точке
оно обладает свойством сохранения углов
между двумя линиями и постоянством
растяжений в малом.
,
называется конформным, если в точке
оно обладает свойством сохранения углов
между двумя линиями и постоянством
растяжений в малом.
Z0
W0
Это значит, что:
При отображении угол между касательными к кривым
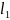 и
и
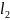 в плоскости
равен углу между касательными к их
образам, кривым
в плоскости
равен углу между касательными к их
образам, кривым
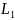 и
и
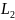 в плоскости
,
то есть
в плоскости
,
то есть
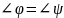 (рис. 1);
(рис. 1);Если в плоскости взять бесконечно малый круг с центром в точке , то ему соответствует бесконечно малый круг в плоскости с центром в точке , то есть конформное отображение обладает свойством консервативности углов и подобия в малом.
Определение
2. Функция
называется однолистной в области
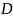 ,
если различным точкам в области
соответствуют различные значения
функции
,
если различным точкам в области
соответствуют различные значения
функции
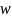 .
Например, линейная функция
.
Например, линейная функция
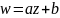 однолистна, а функция
однолистна, а функция
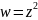 -
двулистна, так как любым двум значениям
-
двулистна, так как любым двум значениям
 и
и
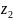 с противоположным знаком соответствует
одно и то же значение w.
Например,
с противоположным знаком соответствует
одно и то же значение w.
Например,
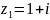 ,
,
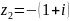 .
.
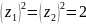 i.
i.
Общие положения теории конформных отображений.
Теорема
Римана. Существует
аналитическая функция
,
отображающая взаимно однозначно и
конформно односвязную область
плоскости
на область
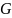 плоскости
,
если только ни одна из этих областей не
совпадает со всей плоскостью с одной
выколотой точкой или со всей расширенной
плоскостью. При этом имеется бесконечное
множество функций, осуществляющих
аналитическое и конформное отображение
области
на область
.
Для обеспечения единственности
отображения функции
требуется выполнение одного из трёх
условий:
плоскости
,
если только ни одна из этих областей не
совпадает со всей плоскостью с одной
выколотой точкой или со всей расширенной
плоскостью. При этом имеется бесконечное
множество функций, осуществляющих
аналитическое и конформное отображение
области
на область
.
Для обеспечения единственности
отображения функции
требуется выполнение одного из трёх
условий:
Точка области перешла в заданную точку области
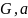 линия, выходящая из точки
линия, выходящая из точки
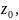 повернулась
на заданный угол α.
повернулась
на заданный угол α.Точка области и точка границы
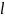 перешли соответственно в точку
области
и в точку
перешли соответственно в точку
области
и в точку
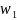 границы
границы
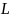 .
.
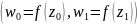
Три граничные точки
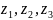 области
перешли в три граничные точки
области
перешли в три граничные точки
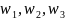 области
.
области
.
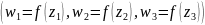 .
При этом, если при движении по границе
от точки
к
.
При этом, если при движении по границе
от точки
к
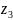 через точку
область
остаётся слева (справа), то при движении
по границе L
от точки
к
через точку
область
остаётся слева (справа), то при движении
по границе L
от точки
к
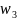 через точку
через точку
 область
также должна оставаться слева (справа).
область
также должна оставаться слева (справа).
Принцип взаимно однозначного соответствия границ.
Пусть - аналитическая функция, заданная в области , которая ограничена гладким или кусочно-гладким контуром и отображает этот контур на некоторый контур L области . Пусть точка z обходит контур так, что область остаётся слева, и соответствующая точка w обходит контур так, что область остаётся слева. Тогда область отобразится на область взаимно однозначно и конформно.
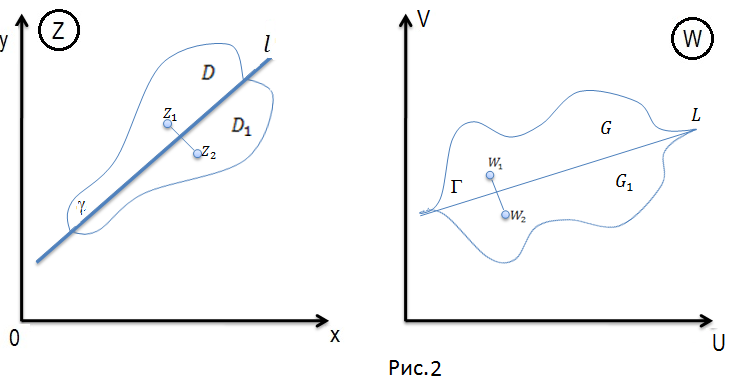
Принцип симметрии.
Пусть
область
,
содержащая в структуре своей границы
некоторый прямолинейный отрезок γ
(конечный или бесконечный), отображается
функцией
на область
так, что γ переходит в прямолинейный
отрезок Г, входящий в границу области
(рис. 2). Пусть
и
- соответствующие прямые, построенные
на этих отрезках. Тогда справедливо
утверждение: если функция
аналитическая в области
,
во всех внутренних точках отрезка γ, то
эта функция аналитическая и в области
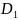 ,
симметричной с
относительно отрезка γ (и прямой
) и обладает тем свойством, что любые
две точки
и
,
(из которых одна лежит в
:
,
симметричной с
относительно отрезка γ (и прямой
) и обладает тем свойством, что любые
две точки
и
,
(из которых одна лежит в
:
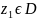 ),
симметричные относительно
,
отображаются в две точки
и
,
симметричные относительно
.
),
симметричные относительно
,
отображаются в две точки
и
,
симметричные относительно
.
Во многих частных случаях для построения отображения некоторой линии , заданной в плоскости , на линию плоскости поступают следующим образом:
а)
Полагают
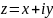 ,
,
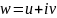 и подставляют в выражение
.
и подставляют в выражение
.
б)
Из этого выражения, выделяя действительную
и мнимую части справа, получают систему
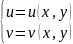 ,
из которой выражают (если это возможно)
,
из которой выражают (если это возможно)
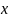 и
и
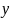 через
через
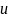 и
и
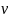 :
:
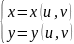 .
.
в) Подставляя эти выражения в уравнение заданной линии , получают уравнение её образа - относительно переменных и .

0
Пример
1. В
области
,
ограниченной контуром
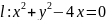 ,
задана функция
,
задана функция
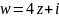 ;. В какую область перейдёт
при отображении функцией
?
;. В какую область перейдёт
при отображении функцией
?
Решение. Пусть , . Тогда
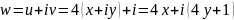 .
.
Следовательно,
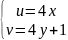 , или
, или
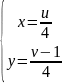 .
.
Подставив полученные выражения в уравнение контура , получим:
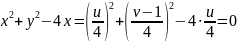
Окончательно:
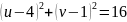 .
.
Ответ: область , ограниченная контуром , отображается функцией
в
круг
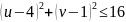 (рисунок 2а).
(рисунок 2а).
Пример
2. На
какую область функция
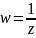 отображает полуполосу:
отображает полуполосу:
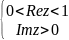 ?
?
Решение. Выделим действительную и мнимую части функции:
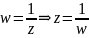 .
Или
.
Или
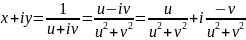 .
.
Тогда,
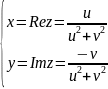
По
первому условию,
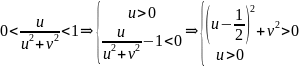
Полученная
система описывает множество точек,
расположенных в правой полуплоскости
UOV
и вне окружности с центром в точке
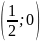 радиусом
радиусом
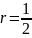 .
.
По
второму условию задачи,
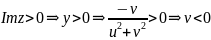 - это множество точек, расположенных в
нижней полуплоскости UOV.
Решением задачи будет пересечение
полученных областей.
- это множество точек, расположенных в
нижней полуплоскости UOV.
Решением задачи будет пересечение
полученных областей.
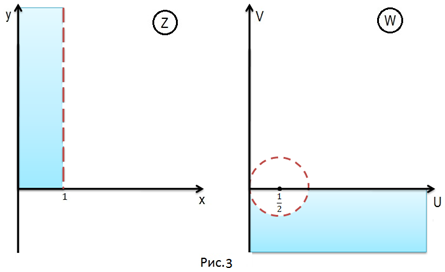
Ответ: полуполоса отображается в область, изображённую на рисунке 3.
