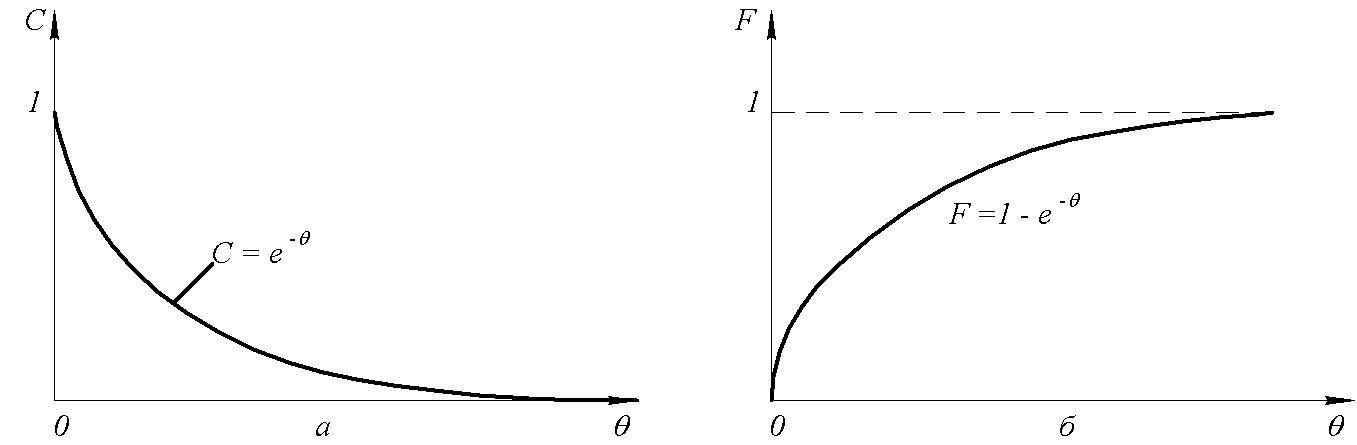4.2. Модель идеального вытеснения

Если модель идеального смешения - модель полностью стохастического движения частиц (предельно неупорядоченного), аналога реального газа, то модель идеального вытеснения представляет собой другую крайность - модель с предельно упорядоченным движением частиц жидкости (рис.4). В соответствии с этой моделью принимается, так называемое, "поршневое" течение жидкости, при котором все частицы потока движутся строго параллельно оси аппарата и время пребывания всех частиц одинаково:

(4.7)

Рис.17. Кривые отклика аппарата идеального смешения на импульсный (а) и ступенчатый (б) ввод трассера

где v=const (т.е. плотность жидкости не изменяется). Если плотность жидкости изменяется по длине аппарата, то среднее время пребывания можно вычислять при условиях на входе в аппарат:

υ (4.8)

где υ - у­с­л­о­в­н­о­е время пребывания. В тех случаях, когда в процессе движения жидкости её плотность меняется (например движение воды в трубках калорифера газовой колонки, движение подогретой нефти в трубопроводе в холодное время года, движение реакционной массы в трубчатом политропическом или адиабатическом химическом реакторе и т.п.) вычисление действительного времени пребывания является непростой задачей.

Уравнение модели идеального вытеснения:

(4.9)

где - координата длины, - средняя скорость потока. Уравнение модели идеального вытеснения удовлетворительно описывает гидродинамику потоков в трубчатых аппаратах при Re >2320 и отношении длины аппарата к диаметру больше 20-100. На рис.18 представлены функции отклика аппарата идеального вытеснения на импульсный и ступенчатый ввод трассера.

Рис.18. Отклики аппарата идеального вытеснения на импульсный (а) и ступенчатый (б) ввод трассера

Неидеальные модели

Между двумя идеальными моделями движения жидкости находятся все реальные аппараты - проточные реакторы с мешалками, трубчатые реакторы, смесители, ректификационные колонны, абсорберы, десорберы, экстрационные аппараты, дегазаторы, отстойники, кожухотрубчатые теплообменники и многие другие. Во всех аппаратах в той или иной мере присутствуют струйное течение, внутренний байпас, обратное и поперечное перемешивание, застойные зоны (см. рис.1). Так, в аппаратах с мешалками наблюдаются застойные зоны, циркуляционные потоки и внутренний байпас (рис.19).

Рис.19. Примеры отклонения течения потока от идеального в проточных аппаратах смешения: (1) вход жидкости; (2) выход; (3) внутренний байпас; (4) циркуляционные потоки; (5) застойные зоны.

В трубчатых аппаратах при турбулентном режиме течения наблюдаются частицы жидкости отстающие от основного потока и даже неподвижные (рис.20). Толщина гидродинамического пограничного слоя зависит и от реологических характеристик жидкости и от скорости движения. В трубчатых или колонных аппаратах при турбулентном режиме те

Рис.20. Примерный профиль скоростей частиц ньютоновой жидкости в трубчатом аппарате При турбулентном режиме движения 1-эпюра скоростей потока; 2-гидродинамический пограничный слой.

чения вследствие турбулентных пульсаций наблюдается неравномерность профиля скоростей (рис.21). Распределение частиц потока по скоростям характеризуется коэффициентом турбулентной диффузии D_турб. В отличие от коэффициента молекулярной диффузии D, являющегося физической характерис тикой вещества и среды, коэффициент турбулентной диффузии D_турб зависит в основном от

Рис.21. Пример неравномерности профиля скоростей частиц ньютоновой жидкости в проточном трубчатом аппарате. 1 - вход потока; 2 - выход

режима течения потока, в частности от критерия Re. Не лучше обстоит дело в ламинарном потоке (рис.22). Поскольку при ламинарном режиме течения в жидкости наблюдается параболический профиль скоростей (строго говоря, в канале круглого сечения - параболлоид), то "помеченные" трассером в момент времени частицы при времени приобретут профиль , при времени - профиль и т.д.

Рис.22. Формирование параболического профиля скоростей и концентраций при ламинарном режиме течения ньютоновой жидкости

Неравномерность профиля концентраций (трассера) и скоростей в сечениях потока приводит к возникновению так называемой тейлоровской диффузии, характеризуемой коэффициентом D_тейл. Этот процесс приводит к тому, что достаточно часто профили концентраций , и так далее практически не наблюдаются. Так же, как и коэффициент турбулентной диффузии D_турб коэффициент тейлоровской диффузии D_тейл зависит, в основном, от режима течения потока. Иногда неравномерность профиля концентраций и скоростей в сечениях потока сильнее перемешивает слои жидкости, чем турбулентная диффузия [10].