2. Метод моментов

2.1. Вероятность событий

Вероятность (лат. probabilitas - правдоподобие, вероятность) - числовая характеристика степени возможности наступления какого-либо определённого события в тех или иных определённых, могущих повториться неограниченное число раз условиях. Вероятность отражает особый тип связей между явлениями, характерных для массовых процессов. Обычно численное значение вероятности находится с помощью определения вероятности: вероятность равна отношению числа исходов , "благоприятствующих" данному событию, к общему числу "равновозможных" исходов . Связь вероятности с частотой события достаточно сложна и зависит от общего числа испытаний . Чем больше число , тем реже встречаются сколько-либо значительные отклонения частоты от вероятности . В соответствии с этим, отчасти неточным, частотным определением вероятности, вероятность осуществления события B будет пределом:

(2.1)

причём частота события является случайной величиной (в отличие от вероятности ).

Таким образом, каждому событию B соответствует некоторое неотрицательное число - его вероятность

(2.2)

причём для невозможного события , для достоверного . В соответствии с этими аксиомами падение подброшенной монеты на землю является достоверным событием, её "взлёт" - невозможное событие, а вероятности выпадения "герба" или "решки" - по 1/2, соответственно (предполагается , что идеальная монета не имеет флуктуаций плотности по объёму, имеет одинаковую толщину и радиус и не может встать на ребро). Другими словами, результат падения монеты (и не только монеты) - случайная величина.

2.2. Распределение вероятностей случайной величины

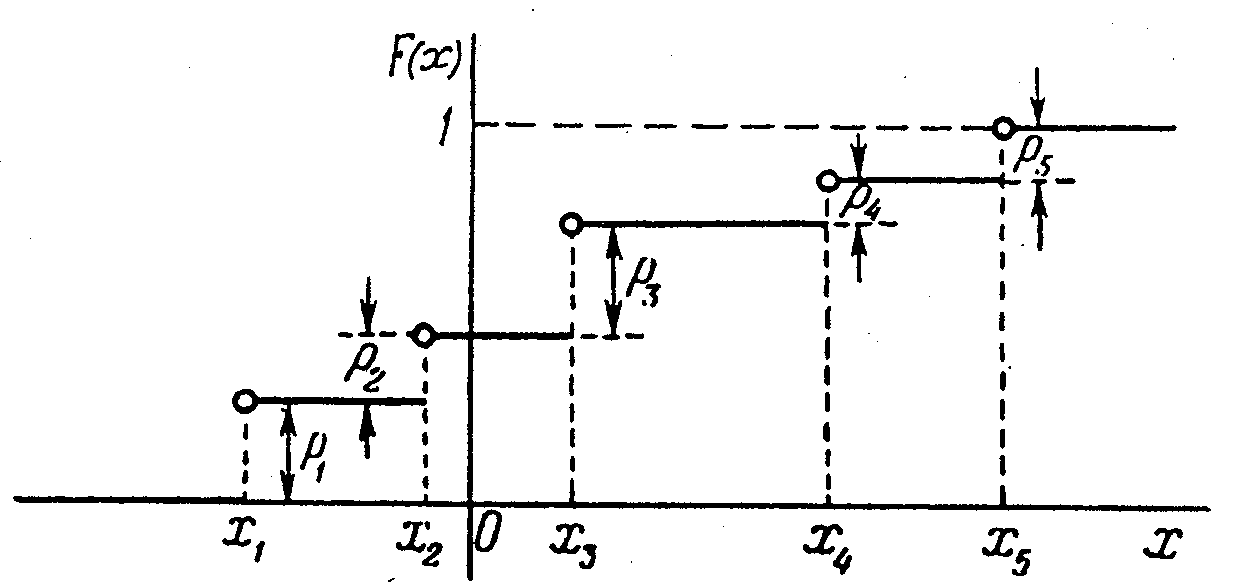
Для дискретных случайных величин характерно то, что они могут принимать те или иные значения только в фиксированных интервалах и их значения в соседних интервалах скачкообразно изменяются (рис.6).

Распределение вероятностей называется дискретным, если случайная величина X может принимать только конкретные возможные значения

которым соответствуют вероятности

Рис. 6 . Функция распределения дискретной случайной величины x. Вероятности pi соответствуют событиям X=xi

, причём .

Наиболее простым примером дискретной системы является система целых чисел 1, 2, 3,..., (в отличие от системы действительных чисел, которая является непрерывной). Значения дискретных случайных величин определяются с абсолютной точностью. Другими словами, результат события однозначен. Например, исход бросания идеальной монеты - "герб" или "решка"; исход бросания идеальной игральной кости (число "очков") - целое число от единицы до шести, исход бросания двух игральных костей - целое число от двух до двенадцати; конечно количество бракованных изделий в партии и др.

Для дискретных случайных величин принято пользоваться вероятностью события , где x - целое число, принадлежащее интервалу (x_min, x_max), а X - случайная величина. Эта вероятность является функцией от x

(2.3)

и называется функцией распределения дискретной случайной величины. Если случайная величина X принимает конечное число дискретных значений (например число очков на гранях игральной кости), то функция распределения вероятностей этой случайной величины представляет собой ступенчатую функцию (рис.7). В соответствии с таким определением вероятность выпадения нуля для идеальной игральной кости равна нулю, вероятность выпадения одного очка равна 1/6, одного или двух - 2/6 и т.д. Вероятность выпадения любого результата от 1 до 6 равна 1, это достоверное событие (см. рис.7). Аналогичны рассуждения при бросании двух игральных костей (рис.8). Соответствующие вероятности см. в статье "Распределение вероятностей".

Добавил строку

Рис.7. Функция распределения числа очков при бросании идеальной кости	Рис.8. Функция распределения числа очков при бросании двух игральных костей

Для непрерывных случайных величин принято пользоваться вероятностью события X<x, где x - произвольное действительное число, принадлежащее интервалу , а X - случайная величина (рис.9).

Эта вероятность является функцией от x:

(2.4)

и называется функцией распределения непрерывной случайной величины

(ср. с (2.3))

Для произвольной функции F(x) если , то (см. рис.9). Максимальное значение F(x)=1. Ордината кривой, соответствующая точке x₁, представляет собой вероятность того, что случайная

Рис.9. Функция распределения вероятностей непрерывной случайной величины

величина X при испытании окажется меньше x₁. Ордината кривой, соответствующая точке x₂, представляет собой вероятность того, что случайная величина X при испытании окажется меньше x₂. Разность двух ординат, соответствующая точкам x₁ и x₂, даёт вероятность того, что значения случайной величины будут лежать в интервале между x₁ и x₂:

. (2.5)

Очевидно, что при предельных значениях аргумента:

На рис.10,а приведена функция распределения вероятностей непрерывной

Рис.10.Распределение положения стрелки часов в случайные моменты времени.

случайной величины - положения стрелки часов в случайные моменты времени. Очевидно, что функция распределения вероятностей является монотонной и неубывающей.

Система действительных чисел является непрерывной системой. Непрерывными случайными величинами являются, например, температура, давление, концентрация, размеры и масса частиц дисперсной фазы, величина пор породы, коэффициент проницаемости и др. В отличие от дискретной случайной величины, каждый результат измерения непрерывной случайной величины X уникален и неповторим, а вероятность получения конкретного точного значения равна нулю, . Это объясняется тем, что при повышении точности измерения одной и той же физической величины всегда будет некоторая разность между двумя любыми измерениями. С другой стороны, если точность собственно измерения физической величины постоянна, но процесс развивается во времени и/или в пространстве (например химическая реакция, движение жидкости, изменение температуры тела и тому подобное), то совокупное влияние множества случайных факторов, сопровождающих исследуемый процесс, в той или иной степени исказит результаты всех измерений и зависимость исследуемой физической величины от независимой не будет идеально гладкой, - экспериментальная зависимость будет представлять собой ломанную линию, другими словами, экспериментальные данные будут образовывать некоторую кривую, имеющую больший или меньший "разброс" значений. При значительном разбросе значений принято говорить, что кривая имеет "выпадающие точки". Повторение процесса в тех же условиях даст близкие результаты, но другие.

Для характеристики непрерывной случайной величины обычно употребляют производную функции распределения - плотность распределения (плотность вероятностей) случайной величины X:

Плотность распределения вероятностей случайной величины является неотрицательной функцией (рис.11).

Рис.11. Плотность распределения непрерывной случайной величины. Общая площадь под кривой равна 1. Площадь заштрихованного участка равна вероятности того, что случайная величина примет значение в интервале x1-x2

Площадь, заштрихованная на графике плотности распределения случайной величины, равна вероятности того, что случайная величина X примет значения в интервале x₁-x₂:

(2.7)

Общая площадь под кривой плотности вероятностей случайной величины равна единице:

(2.8)

Это означает, что случайная величина, имеющая плотность распределения p(x), примет то или иное значение в интервале ; это достоверное событие. На рис.10,б приведена плотность распределения положения стрелки часов в случайные моменты времени. Очевидно, что положение стрелки часов имеет равномерное распределение, т.е. вероятность какого- любо конкретного положения одинакова и равна 1/360. Вероятность любого положения стрелки часов равна 1.