Определение числа ячеек ячеечной модели

Если принять для исследованного аппарата ячеечную модель, то число ячеек можно определить из второго центрального момента по формуле

Таким образом, гидродинамический режим испытанного аппарата будет хорошо описываться ячеечной моделью с числом ячеек n=4

Система из четырех дифференциальных уравнений будет реальной математической моделью испытанного аппарата.

Определение коэффициента продольного перемешивания

Если принять для исследованного аппарата диффузионную однопараметрическую модель, то

В зависимости от типа объекта выбирается формула для расчёта коэффициента продольной диффузии . Для закрытых сосудов границы аппарата совпадают с точками ввода трассера и измерения его концентрации. Формула, связывающая дисперсию параметрической концентрации и критерий Пекле имеет следующий вид [7]:

Отбрасывая второй член правой части уравнения, найдём первое приближение

Подставим значение первого приближения в уравнение (4.15), получим

Очевидно, что тождества нет; примем второе приближение и вновь подставим его в уравнение (4.15):

Продолжая, методом постепенного приближения получим

откуда

Критерий Пекле для данной кривой распределения трассера указывает на то, что исследованному объекту соответствует модель промежуточная между моделью идеального смешения и идеального вытеснения.

5.2. Анализ структуры потоков по результатам испытания ступенчатым возмущением

Аппарат, рассмотренный в примере 5.1, испытан ступенчатым вводом трассера. Концентрация трассера во входном потоке равна 1887710-7 кг/м³. Результаты испытания представлены в табл.3 и на рис.30.

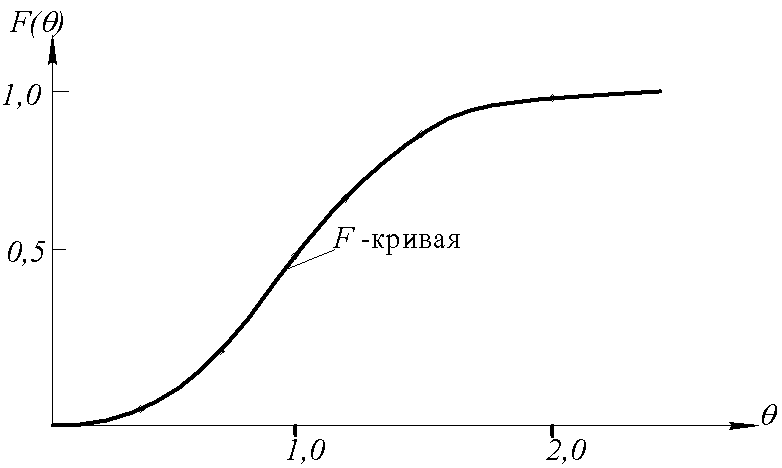
Построение f-кривой

Вычисляем значение функции по формуле (2.14), результаты заносим в табл.3. По результатам расчётов строим интегральную кривую в координатах (рис.31)

Вычисляем значение выражения ; результаты за

носим в табл.3.

Вычисляем начальный момент первого порядка или среднее время пребывания по формуле (3.28):

.

Рис.30. Зависимость концентрации трассера от времени на выходе из проточного аппарата после ступенчатого возмущения

Таблица 3

Зависимость концентрации трассера от времени

при ступенчатом возмущении и результаты расчётов

i	01	02	03	04	05	06	07	08
	0	300	600	900	1200	1500	1800	2100
	0	142	519	991	1415	1698	1840	1887	-
	0	0.08	0.28	0.53	0.75	0.90	0.98	1.0	-
	1.0	0.93	0.73	0.48	0.25	0.1	0.03	0	-
	0	278	435	428	300	150	45	0	1636
	1.93	1.65	1.20	0.73	0.35	0.13	0.03	0	6.0
	300	900	1500	2100	2700	3300	3900	-	-

Вычисляем начальные моменты высших порядков

Рис.31. Кривая отклика проточного аппарата на ступенчатое возмущение в параметрических координатах

Расчёт центральных моментов производится аналогично предыдущему примеру.